Ббк 22.34р30-252.43 2 страница
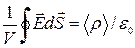 . (1.10)
. (1.10)
Теперь устремим объем V к нулю, стягивая его к интересующей нас точке поля. Очевидно, при этом 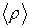 будет стремиться к значению ρ в данной точке поля, а значит, отношение в левой части уравнения (1.10) будет стремиться к ρ/ε0 .
будет стремиться к значению ρ в данной точке поля, а значит, отношение в левой части уравнения (1.10) будет стремиться к ρ/ε0 .
Величину, являющуюся пределом отношения 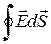 к V при V→0, называют дивергенцией поля
к V при V→0, называют дивергенцией поля  и обозначают
и обозначают 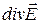 . Таким образом, по определению:
. Таким образом, по определению:
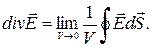 (1.11)
(1.11)
Из определения (1.11) следует, что дивергенция является скалярной функцией координат.
Чтобы получить выражение для дивергенции поля  , надо согласно (1.11) взять бесконечно малый объем V, определить поток вектора
, надо согласно (1.11) взять бесконечно малый объем V, определить поток вектора  сквозь замкнутую поверхность, охватывающую этот объем, и найти отношение этого потока к объему. Полученное выражение для дивергенции будет зависеть от выбора системы координат (в разных системах координат оно оказывается разным). Например, в декартовой системе координат
сквозь замкнутую поверхность, охватывающую этот объем, и найти отношение этого потока к объему. Полученное выражение для дивергенции будет зависеть от выбора системы координат (в разных системах координат оно оказывается разным). Например, в декартовой системе координат
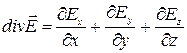 .
.
При V→0 в выражении (1.10) его правая часть стремится к ρ/ε0, а левая — к 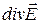 . Следовательно, дивергенция поля
. Следовательно, дивергенция поля  связана с плотностью заряда в той же точке уравнением
связана с плотностью заряда в той же точке уравнением
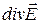 =ρ/ε0 (1.12)
=ρ/ε0 (1.12)
Это уравнение и выражает теорему Гаусса в дифференциальной форме.
В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля  в данной точке зависит только от плотности электрического заряда ρ в той же точке и больше ни от чего. Это одно из замечательных свойств электрического поля. Например, в разных точках поля точечного заряда поле
в данной точке зависит только от плотности электрического заряда ρ в той же точке и больше ни от чего. Это одно из замечательных свойств электрического поля. Например, в разных точках поля точечного заряда поле  отличается друг от друга. Однако, как утверждает теорема Гаусса, сумма этих производных, которая определяет, дивергенцию
отличается друг от друга. Однако, как утверждает теорема Гаусса, сумма этих производных, которая определяет, дивергенцию  , оказывается во всех точках поля (вне самого заряда) равной нулю. В тех точках поля, где дивергенция Е положительна, мы имеем источники поля (положительные заряды), а в тех точках, где она отрицательна, — стоки (отрицательные заряды). Линии вектора
, оказывается во всех точках поля (вне самого заряда) равной нулю. В тех точках поля, где дивергенция Е положительна, мы имеем источники поля (положительные заряды), а в тех точках, где она отрицательна, — стоки (отрицательные заряды). Линии вектора  выходят из источников поля, а в местах стоков они заканчиваются.
выходят из источников поля, а в местах стоков они заканчиваются.
1.4. Потенциал электрического поля
Из механики известно, что любое стационарное поле центральных сил является консервативным, т. е. работа сил этого поля не зависит от пути, азависит только от положения начальной и конечной точки. Именно таким свойством обладает электростатическое поле — поле, образованное системой неподвижных зарядов. Если в качестве пробного заряда, переносимого из точки 1 заданного поля  в точку 2, взять единичный положительный заряд, то элементарная работа сил поля при перемещении
в точку 2, взять единичный положительный заряд, то элементарная работа сил поля при перемещении 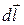 равна
равна 
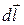 , a вся работа сил поля на пути от точки 1 до точки 2 определяется как
, a вся работа сил поля на пути от точки 1 до точки 2 определяется как
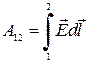 . (1.13)
. (1.13)
Этот интеграл берется по некоторой линии (пути), поэтому его называют линейным.
По произвольному замкнутому пути этот интеграл равен нулю. Интеграл (1.13) по замкнутому пути называют циркуляцией вектора  .
.
Теорема о циркуляции вектора  . Циркуляция вектора
. Циркуляция вектора  в любом электростатическом поле равна нулю, т. е.
в любом электростатическом поле равна нулю, т. е.
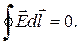 (1.14)
(1.14)
Поле, обладающее свойством (1.14), называют потенциальным. Значит, любое электростатическое поле является потенциальным.
Потенциал.Так как , линейный интеграл (1.13), представляющий собой работу сил поля при перемещении единичного положительного заряда из точки 1 в точку 2, не зависит от пути между этими точками, позволяет утверждать, что в электрическом поле существует некоторая скалярная функция координат j(r), убыль которой
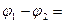
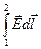 , (1.15)
, (1.15)
где j1 и j2 — значения функции j в точках 1 и 2. Такопределенная величина j(r) называется потенциалом поля. Потенциал — это величина, численно равная потенциальной энергии единичного положительного заряда в данной точке поля. Потенциал j определяется с точностью до произвольной аддитивной постоянной. Значение этой постоянной не играет роли, так как все электрические явления зависят только от напряженности электрического поля. В теории принимают потенциал бесконечно удаленной точки равным нулю ( 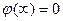 ). Единицей потенциала является вольт (В).
). Единицей потенциала является вольт (В).
Потенциал поля точечного заряда.Формула (1.15) содержит не только определение потенциала j, но и способ нахождения этой функции. Для этого достаточно вычислить интеграл 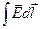 по любому пути между двумя точками и представить затем полученный результат в виде убыли некоторой функции, которая и есть j(r). Формула (1.15) справедлива не только для конечных перемещений, но и для элементарных
по любому пути между двумя точками и представить затем полученный результат в виде убыли некоторой функции, которая и есть j(r). Формула (1.15) справедлива не только для конечных перемещений, но и для элементарных 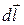 . Тогда согласно этой формуле элементарная убыль потенциала на этом перемещении есть
. Тогда согласно этой формуле элементарная убыль потенциала на этом перемещении есть
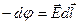 .
.
Если известно поле  (r), то для нахождения j(r) надо представить
(r), то для нахождения j(r) надо представить 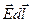 (путем соответствующих преобразований) как убыль некоторой функции j.
(путем соответствующих преобразований) как убыль некоторой функции j.
Найдем таким способом потенциал поля неподвижного точечного заряда:
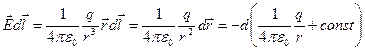 .
.
Потенциал поля точечного заряда таким образом имеет вид (потенциал на бесконечности 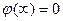 )
)
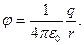 (1.16)
(1.16)
Потенциал поля системы зарядов. Принцип суперпозиций. Потенциал системы неподвижных точечных зарядов
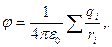 (1.17)
(1.17)
где ri — расстояние от точечного заряда qi до интересующей нас точки поля.
Если заряды, образующие систему, распределены непрерывно, то, как обычно, мы считаем, что каждый элементарный объем dV содержит «точечный» заряд dq. Тогда потенциалнепрерывно распределенного заряда :
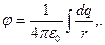 (1.18)
(1.18)
где интегрирование проводится или по всему пространству, или по той его части, которая содержит заряды.
Итак, зная распределение зарядов (дискретное, непрерывное), мы можем в принципе найти потенциал поля любой системы.
Связь между потенциалом и вектором  . Электрическое поле, как известно, полностью описывается векторной функцией
. Электрическое поле, как известно, полностью описывается векторной функцией  (r). Зная ее, мы можем найти силу, действующую на интересующий нас заряд в любой точке поля, вычислить работу сил поля при каком угодно перемещении заряда и др. Связь между j и
(r). Зная ее, мы можем найти силу, действующую на интересующий нас заряд в любой точке поля, вычислить работу сил поля при каком угодно перемещении заряда и др. Связь между j и  можно установить с помощью уравнения
можно установить с помощью уравнения 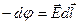 . Пусть перемещение
. Пусть перемещение 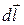 параллельно оси X, тогда
параллельно оси X, тогда 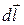 =
= 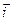 dx, где
dx, где 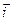 — орт оси X, dx — приращение координаты х. В этом случае
— орт оси X, dx — приращение координаты х. В этом случае
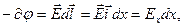
откуда
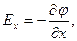 (1.19)
(1.19)
где Ех — проекция вектора Е на орт 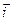 , символ частной производной подчеркивает, что функцию j (х, у, г) надо дифференцировать только по х, считая у и z при этом постоянными.
, символ частной производной подчеркивает, что функцию j (х, у, г) надо дифференцировать только по х, считая у и z при этом постоянными.
Тогда вектор  :
:
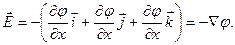 (1.20)
(1.20)
Величина, стоящая в скобках, есть градиент потенциала j (grad j или 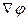 ).
).
О преимуществах потенциала.Потенциал и напряженность однозначно определяют электростатическое поле. Но использование потенциала при расчетах электрического поля имеет ряд преимуществ:
1. Зная потенциал j(r) , можно предельно просто вычислить работу сил поля при перемещении точечного заряда q из точки 1 в точку 2:
А12 = q(j1 -j2 ), (1.21)
где j1 и -j2 — потенциалы в точках 1 и 2. Значит, искомая работа равна убыли потенциальной энергии заряда q в поле при перемещении его из точки 1 в точку 2. Расчет работы сил поля по формуле (1.21) оказывается не только проще, но в некоторых случаях и единственно возможным.
2. Во многих случаях оказывается, что для нахождения напряженности электрического поля легче сначала подсчитать потенциал j и затем взять градиент от него, нежели вычислять  непосредственно. Это весьма существенное преимущество потенциала. Действительно, для вычисления j нужно взять один интеграл, а для вычисления
непосредственно. Это весьма существенное преимущество потенциала. Действительно, для вычисления j нужно взять один интеграл, а для вычисления  — три (ведь это вектор). Кроме того, обычно интегралы для определения j проще, чем для Ех, Еу, Ez. Но в некоторых частных случаях, для небольшого числа задач с достаточно хорошей симметрией нахождение поля
— три (ведь это вектор). Кроме того, обычно интегралы для определения j проще, чем для Ех, Еу, Ez. Но в некоторых частных случаях, для небольшого числа задач с достаточно хорошей симметрией нахождение поля  непосредственно или с помощью теоремы Гаусса часто оказывается значительно проще.
непосредственно или с помощью теоремы Гаусса часто оказывается значительно проще.
Методические указания
1. Для расчета в точке А потенциала электрического поля заряда, распределенного в пространстве методом непосредственного интегрирования необходимо:
1) разбить заряженное тело на бесконечно малые элементы dV (или dS , dl) с элементарным зарядом dq = ρ dV;
2) определить потенциал поля 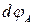 в точке А, создаваемого точечным зарядом dq:
в точке А, создаваемого точечным зарядом dq: 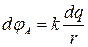 ;
;
3) по принципу суперпозиций потенциал результирующего поля в точке А находится интегрированием по всему объему пространства V, где находится заряд:
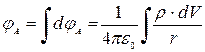 .
.
2. В некоторых частных случаях, для небольшого числа задач с достаточно хорошей симметрией, нахождение потенциала электрического поля  удобно производить через напряженность, которая предварительно находится с помощью теоремы Гаусса. Тогда, использовав связь между напряженностью и потенциалом, получаем ( с учетом, что потенциал на бесконечности
удобно производить через напряженность, которая предварительно находится с помощью теоремы Гаусса. Тогда, использовав связь между напряженностью и потенциалом, получаем ( с учетом, что потенциал на бесконечности 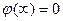 ):
):
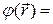
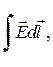
где интегрирование проводится по произвольному (наиболее простому) пути.
Пример 1.5. Потенциал некоторого электрического поля имеет вид 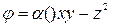 . Найти проекцию вектора
. Найти проекцию вектора  на направление вектора
на направление вектора 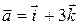 в точке М(2, 1, -3).
в точке М(2, 1, -3).
Решение. Сначала найдем вектор  :
:
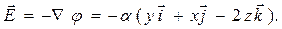
Тогда искомая проекция вектора напряженности
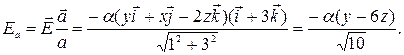
Окончательно получаем значение проекцию вектора  в точке М(2, 1, -3)
в точке М(2, 1, -3)
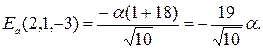
Пример 1.6.Потенциал поля внутри заряженного шара зависит только от расстояния r до его центра по закону φ = ar2 + b, где а и b — постоянные. Найти распределение объемного заряда ρ(r) внутри шара
Решение. Сначала найдем напряженность поля. Согласно (1.20)
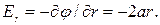
Воспользуемся теоремой Гаусса: 4nr2Er = q/ 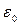 . Дифференциал этого выражения имеет вид:
. Дифференциал этого выражения имеет вид:
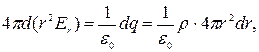
где dq – заряд между сферами, радиусы которых r и r+dr. Отсюда:
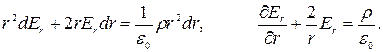
Окончательно получаем:
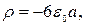
т. е. заряд внутри шара распределен равномерно.
Электрический диполь.Электрический диполь — это система из двух одинаковых по модулю разноименных точечных зарядов +q и -q, находящихся на некотором расстоянии l друг от друга. Когда говорят о поле диполя, то предполагают сам диполь точечным, т. е. считают расстояния r от диполя до интересующих нас точек поля значительно больше l (r>>l).
Поле диполя обладает осевой симметрией, поэтому картина поля в любой плоскости, проходящей через ось диполя, одна и та же и вектор  лежит в этой плоскости.
лежит в этой плоскости.
Потенциал поля диполя, в точке Р (рис. 7, а) определяется по принципу суперпозиций как
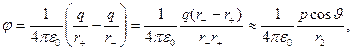 (1.22)
(1.22)
где 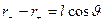 ;
; 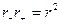 (так как r>>l); r – расстояние от точки Р до диполя (см. рис. 7, а); р = ql — электрический момент диполя. Этой величине сопоставляют вектор, направленный по оси диполя от отрицательного заряда к положительному:
(так как r>>l); r – расстояние от точки Р до диполя (см. рис. 7, а); р = ql — электрический момент диполя. Этой величине сопоставляют вектор, направленный по оси диполя от отрицательного заряда к положительному:
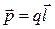 , (1.23)
, (1.23)
где q > 0 и 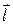 — вектор, направленный в ту же сторону, что и
— вектор, направленный в ту же сторону, что и 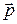 .
.
Из формулы (1.23) видно, что поле и поведение диполя во внешнем поле зависит от его электрического момента 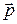 . Следовательно,
. Следовательно, 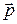 является важной характеристикой диполя.
является важной характеристикой диполя.
Для нахождения поля диполя воспользуемся формулой (1.20), вычислив ее с помощью проекции вектора  на два взаимно перпендикулярных направления — вдоль ортов
на два взаимно перпендикулярных направления — вдоль ортов 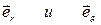 (рис. 7, б):
(рис. 7, б):
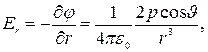
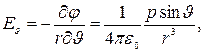 (1.24)
(1.24)
Р r+ r- +q l 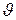 -q Рис.7, а -q Рис.7, а |
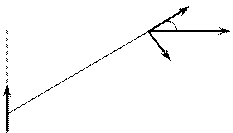  P P 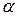  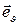 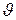 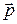 Рис. 7, б Рис. 7, б |
Отсюда модуль вектора  :
:
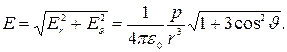 (1.25)
(1.25)
Сила, действующая на диполь. Поместим диполь во внешнее неоднородное электрическое поле. Пусть Е+ и Е_ — напряженности внешнего поля в точках, где расположены положительный и отрицательный заряды диполя. Тогда результирующая сила F, действующая на диполь, равна :
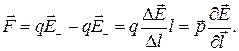 (1.26)
(1.26)
Входящую в это выражение производную принято называть производной вектора по направлению. Знак частной производной подчеркивает, что эта производная берется по определенному направлению — направлению, совпадающему с вектором  или
или  .
.
Момент сил, действующих на диполь. Рассмотрим, как ведет себя диполь во внешнем электрическом поле в своей системе центра масс — будет он поворачиваться или нет. Для этого мы должны найти момент внешних сил относительно центра масс диполя.
По определению, момент сил F+ = qE+ и F_= -qЕ_ относительно центра масс С (рис. 8) равен:
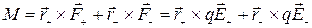 ,
,
где 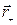 и
и 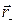 — радиусы-векторы зарядов +q и — q относительно точки С. При достаточно малом расстоянии между зарядами диполя
— радиусы-векторы зарядов +q и — q относительно точки С. При достаточно малом расстоянии между зарядами диполя 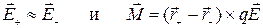 . Остается учесть, что
. Остается учесть, что 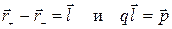 , тогда
, тогда
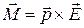 . (1.27)
. (1.27)
+q  l C r+ l C r+   r- -q Рис. 8 r- -q Рис. 8 |
Этот момент сил стремится повернуть диполь так, чтобы его электрический момент 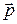 установился по направлению внешнего поля
установился по направлению внешнего поля  . Такое положение диполя является устойчивым. В неоднородном электрическом поле диполь будет вести себя следующим образом: под действием момента сил (1.27) диполь будет стремиться установиться по полю (
. Такое положение диполя является устойчивым. В неоднородном электрическом поле диполь будет вести себя следующим образом: под действием момента сил (1.27) диполь будет стремиться установиться по полю ( 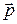 ↑↑
↑↑  ), а под действием результирующей силы (1.26) — переместиться в направлении, где
), а под действием результирующей силы (1.26) — переместиться в направлении, где  по модулю больше. Оба движения будут совершаться одновременно.
по модулю больше. Оба движения будут совершаться одновременно.
Пример 1.6. Найти силу взаимодействия двух точечных диполей с моментами 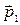 и
и 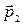 , если векторы
, если векторы 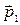 и
и 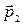 направлены вдоль прямой, соединяющей диполи, и расстояние между последними равно l.
направлены вдоль прямой, соединяющей диполи, и расстояние между последними равно l.
Решение. Согласно (1.26),
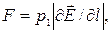
где Е — напряженность поля диполя 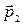 , определяемая первой из формул (1.25):
, определяемая первой из формул (1.25):
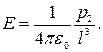
Взяв производную последнего выражения по r и подставив ее в формулу для F, получим:
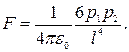
Задачи для самостоятельного решения
Напряженность электрического поля. Принцип суперпозиций.
1.1. Два заряда, q1 и q2, находятся в точках с радиус - векторами 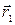 и
и 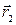 соответственно. Найти, каким должен быть третий заряд q3 и каким должен быть его радиус-вектор
соответственно. Найти, каким должен быть третий заряд q3 и каким должен быть его радиус-вектор 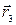 , чтобы суммарная сила взаимодействия для всех зарядов была нулевой.
, чтобы суммарная сила взаимодействия для всех зарядов была нулевой.
1.2. Два небольших одинаково заряженных шарика массой m подвешены к одной точке на шелковых нитях, образующих между собой малый угол 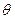 и находятся на одном уровне. Найти скорость утечки заряда с каждого шарика, если скорость сближения шариков постоянна и равна V.
и находятся на одном уровне. Найти скорость утечки заряда с каждого шарика, если скорость сближения шариков постоянна и равна V.
1.3. Тонкое проволочное кольцо R=100мм имеет электрический заряд q=50мкКл. Каково будет приращение силы, растягивающей проволоку, если в центре кольца поместить точечный заряд q0 =7.0 мкКл ?
1.4. В вершинах квадрата с диагональю 2l=100 мм находятся одинаковые по модулю (q = 2.5мкК) точечные заряды, знаки которых при обходе квадрата расположены в порядке ‘+’,’+’,’-‘,’-‘. Найти напряжённость Е электрического поля в точке, отстоящей на расстоянии х=50 мм от центра квадрата и расположенной симметрично относительно вершин.
1.5. Полубесконечный круглый цилиндр радиусом R заряжен равномерно по поверхности так, что на единицу его длины приходится заряд l. Найти напряженность электрического поля в центре основания цилиндра.
1.6. Тонкое непроводящее кольцо радиусом R заряжено с линейной плотностью l=l0cosj, где l0 постоянная, j — азимутальный угол. Найти модуль напряженности электрического поля :
а) в центре кольца ;
б) на оси кольца в зависимости от расстояния x от до его центра. Исследовать полученное выражение при x>>R.
1.7. Диск радиусом R заряжен равномерно с поверхностной плотностью σ. Определить напряженность поля Е в точке, находящейся на расстоянии d от диска, на перпендикуляре, проходящем через центр диска.
Теорема Гаусса
1.8. Длинная прямая равномерно заряженная нить имеет заряд λ на единицу длины. Найти модуль и направление электрического поля в точке, которая отстоит от нити на расстоянии y и находится на перпендикуляре к нити, проходящем через один из её концов.
1.9. Две скрещивающиеся, взаимно перпендикулярные нити бесконечной длины заряжены равномерно с линейной плотностью 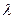 . Найти силу их взаимодействия.
. Найти силу их взаимодействия.
1.10 Напряженность электрического поля 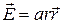 , где a- постоянная, r — расстояние от центра поля. Найти плотность зарядов ρ(r), создающих это поле.
, где a- постоянная, r — расстояние от центра поля. Найти плотность зарядов ρ(r), создающих это поле.
1.11. Из трех концентрических бесконечно тонких металлических сфер с радиусами R1 < R2 < R3 крайние заземлены, а средней сфере сообщен электрический заряд Q. Найти напряженность электрического поля во всех точках пространства. Сферы находятся в вакууме.
1.12. В равномерно заряженной сфере вырезано малое отверстие. Какова напряженность поля в центре отверстия?
1.13. Определить напряженность поля Е внутри и вне безграничного плоского слоя толщиной d, в котором равномерно распределен положительный заряд с объемной плотностью ρ.
