Арифметика остатков
Зафиксируем некоторое натуральное число 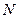 , которое назовем модулем. Если разность двух чисел
, которое назовем модулем. Если разность двух чисел 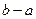 делится на
делится на 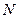 нацело, то пишут
нацело, то пишут 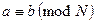 и говорят, что числа
и говорят, что числа 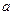 и
и 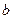 сравнимы по модулю
сравнимы по модулю 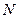 . В этом случае числа
. В этом случае числа 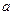 и
и 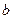 имеют одинаковый остаток от деления на
имеют одинаковый остаток от деления на 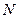 . Если ясно, по какому модулю происходит сравнение чисел
. Если ясно, по какому модулю происходит сравнение чисел 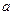 и
и 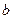 , то просто пишут
, то просто пишут 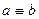 .
.
Будем использовать 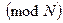 как обозначение оператора модуля на множестве целых чисел, который вычисляет наименьшее натуральное число, сравнимое с данным по модулю
как обозначение оператора модуля на множестве целых чисел, который вычисляет наименьшее натуральное число, сравнимое с данным по модулю 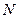 . Например,
. Например, 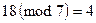 ,
, 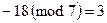 .
.
Все возможные остатки от деления чисел на 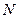 образуют множество
образуют множество 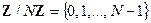 . Очевидно, что
. Очевидно, что 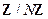 - множество значений оператора модуля
- множество значений оператора модуля 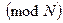 . Некоторые авторы обозначают это множество
. Некоторые авторы обозначают это множество 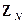 .
.
Поскольку все сравнимые между собой по модулю 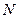 целые числа имеют один и тот же остаток, будем считать, что элемент
целые числа имеют один и тот же остаток, будем считать, что элемент 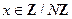 изображает целый класс чисел вида
изображает целый класс чисел вида 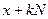 , где
, где 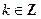 . Таким образом, оперируя с целыми числами по модулю
. Таким образом, оперируя с целыми числами по модулю 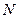 , будем считать все сравнимые между собой числа равными друг другу и вместо знака «
, будем считать все сравнимые между собой числа равными друг другу и вместо знака « 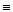 » использовать знак «=».
» использовать знак «=».
На множестве 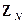 есть две основные операции – сложение и умножение. Они определяются обычным путем: если
есть две основные операции – сложение и умножение. Они определяются обычным путем: если 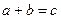 и
и 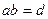 , то
, то 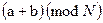 =
= 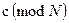 и
и 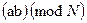 =
= 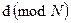 . Например,
. Например, 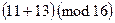 =
= 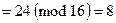 и
и 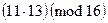
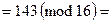
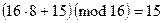 .
.
Сложение и умножение по модулю 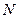 работают почти так же, как арифметические операции над вещественными и целыми числами. Они обладают следующими свойствами.
работают почти так же, как арифметические операции над вещественными и целыми числами. Они обладают следующими свойствами.
1. Замкнутость сложения: 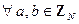 :
: 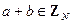 .
.
2. Ассоциативность сложения: 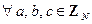 :
: 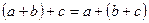 .
.
3. Нуль является единичным (нейтральным) элементом по сложению : 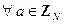 :
: 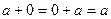 .
.
4. Всегда существует обратный (противоположный) элемент по сложению: 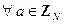 :
: 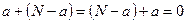 .
.
5. Коммутативность сложения: 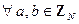 :
: 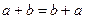 .
.
6. Замкнутость умножения: 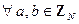 :
: 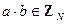 .
.
7. Ассоциативность умножения: 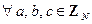 :
: 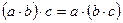 .
.
8. Число 1 является единичным (нейтральным) элементом по умножению: 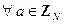 :
: 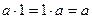 .
.
9. Умножение и сложение связаны законом дистрибутивности: 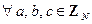 :
: 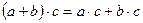 .
.
10. Коммутативность умножения: 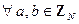 :
: 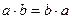 .
.
Определение. Кольцом называется множество 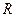 с двумя операциями (сложение и умножение), которые обладают свойствами 1-9.
с двумя операциями (сложение и умножение), которые обладают свойствами 1-9.
Если умножение в кольце окажется коммутативным, то такое кольцо называется коммутативным кольцом.
Множество остатков 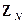 с операциями сложения и умножения является коммутативным кольцом, которое часто называется кольцом вычетов по модулю
с операциями сложения и умножения является коммутативным кольцом, которое часто называется кольцом вычетов по модулю 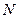 .
.
