Методы расчета надежности невосстанавливаемых систем и элементов
Устройство состоит из элементов, показатель надежности (ПН) которых известен.
Существует несколько методов расчета показателя надежности устройств:
1) структурная схема расчета надежности. Наиболее употребительный метод.
2) логико-вероятностный метод (метод И.А. Рябинина). Метод нашел ограниченное применение;
3) топологический метод. Применяется для расчета вероятностей состояний сложных систем; но по своей сути использует формулу Мезона для сигнальных графов с некоторыми изменениями в связи со спецификой задач расчета надежности;
4) метод сигнального графа надежности. Производится запись системы дифференциальных уравнений (по Колмогорову), отражающих динамику переходов между состояниями системы. Дифференциальные уравнения обычно представляются в изображениях по Лапласу и рисуется граф переходов, для которого записывается система алгебраических уравнений. Поскольку граф сигнальный, для поиска вероятностей сожжет использоваться опять формула Мезона (но со спецификой), либо система уравнений решается по методу, например, Крамера.
2.1. Структурная схема.
Структурная схема расчета надежности составляется исходя из причинно-следственных связей отказа элемента и отказа устройства.

Рис. 3. Последовательное соединение элементов
Вероятность отказа для элемента А составляет 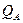 , для элемента В -
, для элемента В - 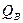 .
.
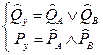 (2.1)
(2.1)
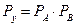 (2.2)
(2.2)
Если отказ устройства имеет место, когда отказывает элемент А или В, то на структурной схеме расчета надежности это обозначается последовательным соединением этих элементов.
Если имеет место отказ обоих элементов, то картина несколько изменится:
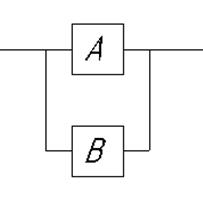
Рис. 4. Параллельное соединение элементов.
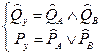 (2.3)
(2.3)
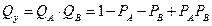 (2.4)
(2.4)
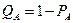
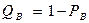
отсюда
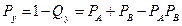 (2.5)
(2.5)
Могут быть так же соединения типа:
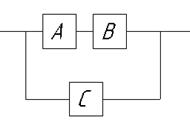
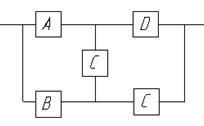
Пример: рассчитать показатель надежности системы
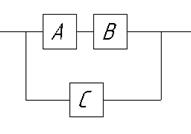
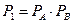
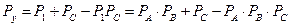
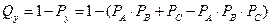 .
.
Соединения, которое не сводится к последовательно-параллельным.
Существует два основных подхода к преобразованию и расчету таких схем:
1) Метод разложения по базовому элементу:
а)
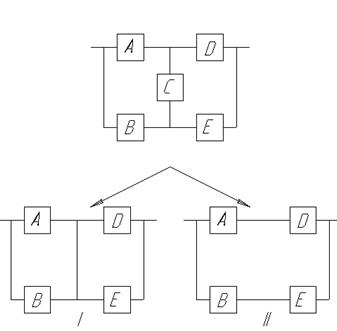
I) предполагаем, что 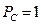
II) предполагаем, что 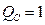
б) 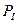 ,
, 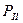 - известно.
- известно.
в) используя теорему о вероятности несовместных событий получим:
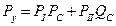
2) преобразование звезда в треугольник или треугольника в звезду.
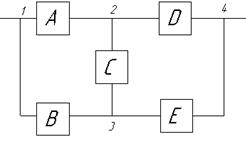
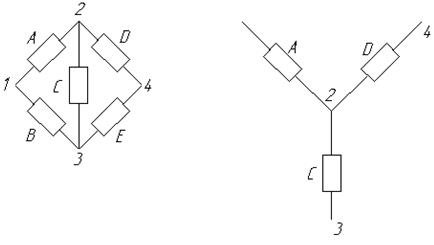
Рис. 5. Преобразования треугольника в звезду и обратно.
Преобразование треугольника в звезду позволяет привести к последовательно-параллельному соединению.
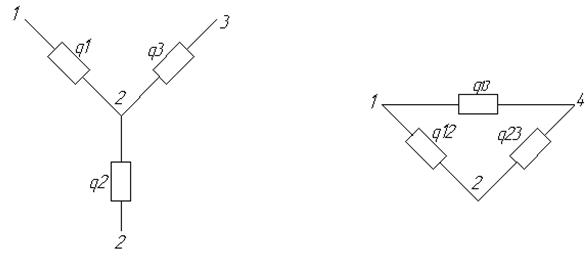
Рис. 6. Расчетная схема соединения «треугольника» и «звезды».
Используют только вероятности отказа.
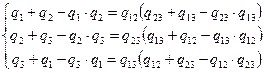 (2.6)
(2.6)
Учитывая, что 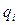 ,
, 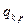 много меньше 1, то
много меньше 1, то 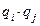 - величина третьего порядка малости.
- величина третьего порядка малости.
Система с учетом отбрасывания элементов 2-го и 3-го порядка малости:
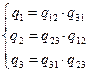 (2.7)
(2.7)
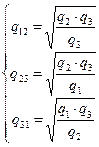 (2.8)
(2.8)
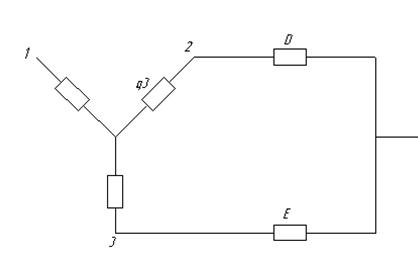
Рис. 7. Схема после преобразования треугольника в звезду.
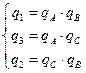 (2.9)
(2.9)
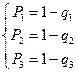 (2.10)
(2.10)
2.2. Логико-вероятностный метод
Идея метода (метод Рябинина) заключается в том, что:
- отказ и исправное состояние связываются с логическими переменными, принимающими значение «0» и «1».
- условие работоспособности устройства (системы) через работоспособность элементов записывается в виде логических функций;
- осуществляется переход от логических функций к записи вероятности безотказной работы устройства через вероятности безотказной работы элементы.
Метод имеет ограничения. Логическая функция должна иметь бесповторную ортогональную форму, что сильно сужает класс решаемых задач.
Рассмотрим метод более подробно.
1)
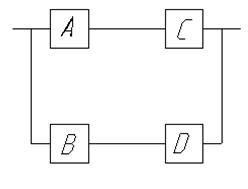
применяется карта Карно или диаграмма Вейча.
| Д | |||||||
| В | |||||||
| А | |||||||
| С |
Таблица заполняется исходя из работоспособности устройства с элементами.
Запись сделана по совершенно дизъюнктивной нормальной форме.
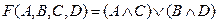
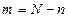
Бесповторная ортогональная форма – каждый конъюнкт входит один раз.
Бесповторность обеспечивает правильность расчета вероятностей. Например, логическое выражение 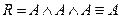 (с точки зрения логики), но после подстановки вместо
(с точки зрения логики), но после подстановки вместо 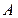 вероятностей получается
вероятностей получается 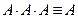 .
.
Если выражение не бесповторное, тогда оценка вероятностей будет заниженной.
Аналогично при расчете дизъюнкций (эквивалент параллельного соединения), вероятность завышена.
Поэтому данный метод должен в общем случае рассматриваться как оценочный (может показать границу сверху или снизу).
Ортогональность – это значит, что дизъюнкты должны обладать свойством, что если один дизъюнкт равен «1», то остальные должны быть «0».
В дальнейшем будем требовать только минимальности формы логического выражения. Это приводит к ошибкам в оценке вероятности, но, как правило, не слишком значимым.
2) Алгоритмизация логической функции.
Это замена:
а) логических умножений на алгебраические умножения 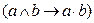 ;
;
б) замена дизъюнкций 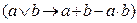 ;
;
в) замена отрицаний 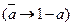 ;
;
г) имена переменных заменяются на вероятности безотказной работы
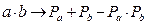 ;
;
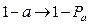 ;
;
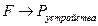
для данного примера:
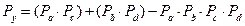 - этот результат точный, т.к. выражение бесповторное.
- этот результат точный, т.к. выражение бесповторное.
Пример 2.
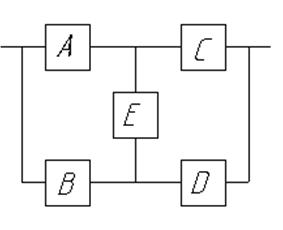
Рис. 8. Структурная схема к примеру 2.
| D | |||||||||||
| В | |||||||||||
| A | |||||||||||
| C | |||||||||||
| E | E |
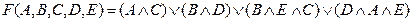
избавимся от В:
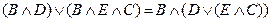
Если элементы очень надежные, то повторность в принципе не влияет.
Некоторые другие примеры рассматриваются в теме «Расчет показателей надежности систем с восстановлением».
