Потокосцепление. Индуктивность и взаимная индуктивность

При анализе электрических и магнитных полей потокосцепление y одного контура с током I определяется магнитным потоком (величина которого пропорциональна току), сцепляющимся с этим контуром. Такой поток называют потоком самоиндукции. Потокосцепление самоиндукции данного контура обозначают y_L

(3.14)

Коэффициент пропорциональности L называют собственной индуктивностью контура. Единицей измерения индуктивности является генри (Гн).

Собственная индуктивность всегда положительна.

Если магнитный поток, сцепляющийся с рассматриваемым контуром (например, первым), создается током I₂ во втором контуре, то для линейной среды потокосцепление будет пропорционально току I₂. При этом потокосцепление называют потокосцеплением взаимной индукции и обозначают y₁₂ или y_1М

.

Величину М₁₂ называют взаимной индуктивностью контуров.

Магнитные потоки, создаваемые постоянными токами, определяют статические индуктивности, которые зависят от геометрических размеров контуров, их взаимного расположения, магнитной проницаемости контуров и среды.

Потокосцепление катушки, содержащей N витков (при условии, что магнитный поток сцепляется со всеми витками) можно определить и так

Если магнитное поле создается токами, протекающими в n контурах, которые расположены в среде с m = const, то потокосцепление y_k с k – м контуром рассчитывается как сумма потокосцепления самоиндукции, определяемого током I_k в этом же контуре, и потокосцеплений взаимной индукции, определяемых токами в остальных контурах:

Энергия магнитного поля. Распределение энергии

Энергия магнитного поля распределяется во всем объеме поля. При этом каждая точка поля характеризуется объемной плотностью энергии магнитного поля

(3.15)

Энергия магнитного поля в некотором объеме V (с учетом выражения (3.15)) равна:

Энергия магнитного поля системы n контуров с токами равна полусумме произведений токов в контурах на потокосцепление контуров

Так, энергия магнитного поля одного контура или катушки с током определяется (с учетом выражения (3.14)) следующим образом:

Энергия системы двух контуров, связанных друг с другом посредством магнитного поля, равна:

Электромагнитная сила

Проводники с электрическими токами, расположенные в магнитном поле, испытывают механические силы. Эти механические силы называют электромагнитными силами или электродинамическими силами.

.

Здесь g -обобщенная координата.

Таким образом, электромагнитная сила, стремящаяся изменить данную координату g системы, равна изменению энергии магнитного поля, отнесенному к единице производимого силой изменения координаты в предположении, что либо потокосцепления контуров, либо токи во всех контурах сохраняются неизменными.

Представим несколько выражений для определения электромагнитной силы. Так, электромагнитная сила со стороны внешнего поля, испытываемая объемом V проводника с плотностью тока 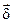, определяется выражением:

Электромагнитная сила со стороны внешнего поля, испытываемая отрезком линейного проводника длиной l с током I, равна:

.

В случае если проводник с током расположен в однородном поле, то сила, воздействующая на проводник, может быть определена с помощью формулы:

Здесь вектор направлен по току.

Отметим, что направление силы можно также определить по правилу левой руки.

Электромагнитная сила, действующая на каждый из двух параллельных проводников (на длине l) с токами I₁ и I₂, равна:

При этом, если токи одного направления, то проводники притягиваются друг к другу, а если разного – отталкиваются.

Объемная плотность электромагнитной силы, действующей на магнетик (среды, способной намагничиваться)

Расчет индуктивностей

Общее выражение для взаимной индуктивности двух контуров произвольной формы (рис. 3.5), выполненных из немагнитного материала и расположенных в воздухе, выглядит следующим образом:

где V₁ и V₂ – объемы пространства, занимаемого первым и вторым контуром; r – расстояние от элемента объема dv₁ первого контура до элемента объема dv₂ второго контура; - вектор плотности тока в точках элемента объема dv₁; - вектор плотности тока в точках элемента объема dv₂.

Как было отмечено выше, при m = const взаимная индуктивность не зависит от токов в контурах. Наличие токов в последнем выражении не противоречит этому положению, поскольку при постоянных токах их можно внести под знаки интегралов, и тогда в подынтегральном выражении получим отношение плотности тока к соответствующему току, которое определяется только формой проводника.

Общее выражение для собственной индуктивности контура можно получить, пользуясь общим выражением для взаимной индуктивности двух контуров. Для этого необходимо представить два совершенно одинаковых контура, сближающихся до полного слияния так, что один из них занимает объем другого. После такого слияния, по существу, уже остается только один контур. Из выражения для М₂₁ нетрудно получить выражение для L такого контура, положив I₁ = I₂ = I и V₁ = V₂ = V. Имеем

причем 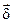- плотность тока в элементе dv; - плотность тока в элементе dv^/ одного и того же проводника; r – расстояние между этими элементами объема. Интегрирование производится дважды по всему объему проводника V.

Формулы для индуктивности весьма упрощаются для контуров из линейных проводников, поперечные размеры сечений которых весьма малы. При вычислении собственной индуктивности таких проводников ее подразделяют на внутреннюю (L_ВТ) и внешнюю (L_ВШ) и общую индуктивность определяют путем их суммирования.

Ниже приведены выражения для индуктивностей простейших систем.

Индуктивность тонкого цилиндрического проводника длиной l и радиусом R (длина много больше радиуса)

.

Индуктивность отрезка цилиндрического проводника длиной l и радиусом R

Индуктивность двухпроводной линии на длине l

.

Здесь D – расстояние между проводами; R – радиус проводов (R << D).

Индуктивность параллельных цилиндров длиной l, с радиусами R₁ и R₂ и расстоянием между осями D

.

Индуктивность круглого кольца радиусом r из тонкого цилиндрического провода диаметром d

Если провод выполнен из неферромагнитного материала, то

Индуктивность прямоугольной рамки из тонкого круглого провода

Здесь а и b – длины сторон рамки; d – диагональ рамки; r – радиус провода (r << а; r << b).