Аналітичне подання булевих функцій
Вище згадувалось, що існує аналітичний спосіб (форма) задання булевих функцій, були розглянуті прості приклади. Тут розглянемо універсальні (канонічні) форми представлення, які дають можливість одержати аналітичну форму безпосередньо виходячи з таблиці істинності для довільної булевої функції. Ця форма у подальшому може бути спрощена. Оскільки між множиною аналітичних представлень і множиною цифрових схем, які реалізують булеву функцію, існує взаємно однозначна відповідність, то відшукання канонічних форм представлення булевої функції являється початковим етапом синтезу цифрової схеми, яка її реалізує. Найбільш широкого застосування набула досконала диз’юнктивна нормальна форм (ДДНФ).
Розглянемо, як можна здійснити перехід від табличного задання булевої функції до аналітичного її представлення.
Звертаємо увагу, що надалі, з метою спрощення записів, замість символу диз’юнкції “ 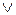 ” будемо вживати символ “+” і трактувати його як логічне додавання, символ кон’юнкції ”
” будемо вживати символ “+” і трактувати його як логічне додавання, символ кон’юнкції ” 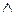 ” будемо опускати або замінювати символом ”∙” і трактувати це як логічне множення задане за замовчуванням або явне, а операцію інверсії будемо позначати символом ”¯”.
” будемо опускати або замінювати символом ”∙” і трактувати це як логічне множення задане за замовчуванням або явне, а операцію інверсії будемо позначати символом ”¯”.
10. Диз’юнктивна форма. Припустимо, що маємо булеву функцію від n аргументів (змінних), тобто n-місну булеву функцію. Так як будь-яка змінна 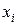 може приймати одне із двох значень 0 або 1, то двійкові набори значень змінних (як уже відмічалось) можна розглядати як записи деяких цілих чисел у двійковій системі числення, тобто записи вигляду
може приймати одне із двох значень 0 або 1, то двійкові набори значень змінних (як уже відмічалось) можна розглядати як записи деяких цілих чисел у двійковій системі числення, тобто записи вигляду 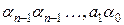 . Кожному такому запису можна поставити у відповідність десяткове число
. Кожному такому запису можна поставити у відповідність десяткове число 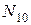 , яке одержується за формулою
, яке одержується за формулою
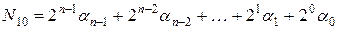 .
.
Це число, як відомо, є номером відповідного набору. Так, для чотиримісної булевої функції номером набору 1101 є число
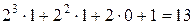 .
.
Нагадаємо, що номери наборів n-місної булевої функції змінюються від 0 до 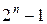 .
.
Розглянемо деякий фіксований набір змінних 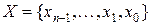 , на якому задана функція алгебри логіки.
, на якому задана функція алгебри логіки.
Означення 1.Кон’юнкція змінних з набору X або їх заперечень вигляду 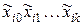 , де
, де 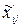 означає або
означає або 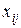 , або
, або 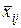 (j=0,1,...,k), називається елементарною кон’юнкцією, якщо в ній кожна змінна зустрічається не більше одного разу.
(j=0,1,...,k), називається елементарною кон’юнкцією, якщо в ній кожна змінна зустрічається не більше одного разу.
До елементарних кон’юнкцій відносять також вирази, що складаються з однієї змінної (в прямій або інверсній формі), розглядаючи їх як одномісні елементарні кон’юнкції. Константу 1 зручно розглядати як 0-місну елементарну кон’юнкцію. Наприклад, елементарними кон’юнкціями є: 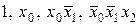 , а вирази
, а вирази 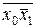 ,
, 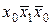 елементарними кон’юнкціями не являються.
елементарними кон’юнкціями не являються.
Означення 2.Диз’юнкція елементарних кон’юнкцій вигляду:
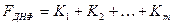 ,
,
де 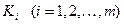 – елементарні кон’юнкції – називається диз’юнктивною нормальною формою (ДНФ).
– елементарні кон’юнкції – називається диз’юнктивною нормальною формою (ДНФ).
Наприклад, функція 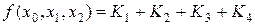 , де
, де 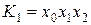 ,
, 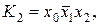
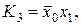
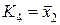 – є диз’юнктивною нормальною формою (ДНФ).
– є диз’юнктивною нормальною формою (ДНФ).
Означення 3.Елементарна n-місна кон’юнкція, що включає в себе всі змінні набору X (в прямій або інверсній формі), називається мінтермом(кон’юнктивним термом) або конституентою одиниці.
Таким чином мінтерми для n-місної функції являють собою логічний добуток вигляду 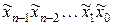 , де кожна із змінних може входити в прямій або інверсній формі. З цього випливає, що максимальне число різних мінтермів для набору з n змінних дорівнює
, де кожна із змінних може входити в прямій або інверсній формі. З цього випливає, що максимальне число різних мінтермів для набору з n змінних дорівнює 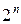 . Неважко встановити, що кожний конкретний мінтерм приймає значення 1 тільки на єдиному наборі, а на всіх інших наборах – приймає значення 0.
. Неважко встановити, що кожний конкретний мінтерм приймає значення 1 тільки на єдиному наборі, а на всіх інших наборах – приймає значення 0.
Наприклад, логічні добутки (кон’юнкції): 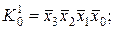
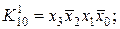
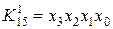 являються мінтермами змінних
являються мінтермами змінних 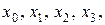 які приймають значення 1 на наборах: 0000, 1010, 1111, яким відповідають десяткові номери: 0, 10, 15. Зрозуміло, що на інших 12 наборах, кожний із розглянутих мінтермів приймає значення 0.
які приймають значення 1 на наборах: 0000, 1010, 1111, яким відповідають десяткові номери: 0, 10, 15. Зрозуміло, що на інших 12 наборах, кожний із розглянутих мінтермів приймає значення 0.
Означення 4.Диз’юнкція вигляду:
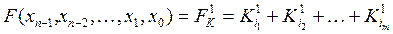 ,
,
де 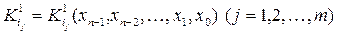 – усі конституанти одиниці функції
– усі конституанти одиниці функції 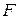 називається досконалою диз’юнктивною нормальною формою (ДДНФ).
називається досконалою диз’юнктивною нормальною формою (ДДНФ).
Якщо прийняти до уваги, що диз’юнкція вигляду 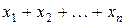 дорівнює 1, коли хоча би одна зі змінних приймає значення 1, то можна легко виразити будь-яку булеву функцію як диз’юнкцію мінтермів (конституант одиниці), які відповідають тим наборам, на яких функція дорівнює 1.
дорівнює 1, коли хоча би одна зі змінних приймає значення 1, то можна легко виразити будь-яку булеву функцію як диз’юнкцію мінтермів (конституант одиниці), які відповідають тим наборам, на яких функція дорівнює 1.
Теорема.Будь-яку булеву функцію 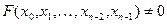 (тотожно) можна єдиним способом представити у вигляді досконалої диз’юнктивної нормальної форми.
(тотожно) можна єдиним способом представити у вигляді досконалої диз’юнктивної нормальної форми.
Доведення. Розглянемо логічну формулу
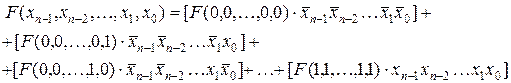 (1)
(1)
Формула (1) є диз’юнкцією 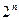 елементарних кон’юнкцій. Перший член формули – це кон’юнкція значення функції на нульовому наборі:
елементарних кон’юнкцій. Перший член формули – це кон’юнкція значення функції на нульовому наборі: 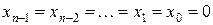 та заперечень усіх змінних цього набору. Другий член формули – кон’юнкція значення функції на першому наборі:
та заперечень усіх змінних цього набору. Другий член формули – кон’юнкція значення функції на першому наборі: 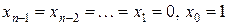 , заперечень перших
, заперечень перших 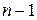 аргументів цього набору та аргументу
аргументів цього набору та аргументу 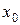 без заперечення. В останньому члені маємо кон’юнкцію значення функції на останньому наборі аргументів
без заперечення. В останньому члені маємо кон’юнкцію значення функції на останньому наборі аргументів 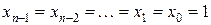 та цих аргументів без заперечення.
та цих аргументів без заперечення.
З наведеної формули бачимо, що коли в наборі аргумент набуває значення 0, то в елементарну кон’юнкцію, яка знаходиться в квадратних дужках, він входить із запереченням, а якщо 1 – то без заперечення.
Справедливість цієї формули очевидна. Якщо, наприклад, візьмемо набір 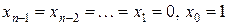 , то в лівій частині матимемо
, то в лівій частині матимемо 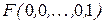 . У правій частині всі елементарні кон’юнкції, крім другої, дорівнюють нулю, а друга набуде вигляду
. У правій частині всі елементарні кон’юнкції, крім другої, дорівнюють нулю, а друга набуде вигляду
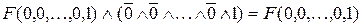 ,
,
тобто те саме, що і в лівій частині.
Таким чином, при будь-яких наборах, в лівій і правій частинах завжди будемо мати одинакові вирази.
З доведеної теореми випливає, що будь-яку булеву функцію можна однозначно представити в аналітичному вигляді
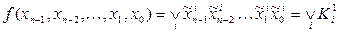 , (2)
, (2)
де символ “ 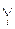 ” означає логічну суму мінтермів, на яких функція дорівнює 1. Одержана форма і є ДДНФ.
” означає логічну суму мінтермів, на яких функція дорівнює 1. Одержана форма і є ДДНФ.
Приклад 5. Записати ДДНФ для функцій, заданих таблицею істинності (табл. 12). 
Таблиця 12
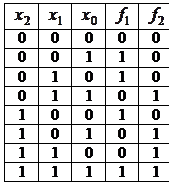 Розв’язання. Запишемо ДДНФ у вигляді логічної суми логічних добутків значень функції на відповідні мінтерми, які записуються у вигляді елементарних кон’юнкцій, утворених змінними у прямій або інверсній формі: якщо значення змінної 1, то пряма форма, а якщо 0, то – інверсна.
Розв’язання. Запишемо ДДНФ у вигляді логічної суми логічних добутків значень функції на відповідні мінтерми, які записуються у вигляді елементарних кон’юнкцій, утворених змінними у прямій або інверсній формі: якщо значення змінної 1, то пряма форма, а якщо 0, то – інверсна.
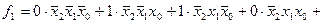
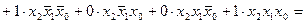
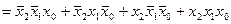 .
. 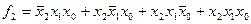 .
.
Легко бачити, що функція 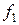 є не що інше як сума за модулем 2 трьох змінних, тобто
є не що інше як сума за модулем 2 трьох змінних, тобто 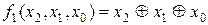 .
.
Функція 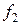 називається мажоритарною (вона приймає значення, яке приймає більшість змінних) і позначається
називається мажоритарною (вона приймає значення, яке приймає більшість змінних) і позначається 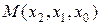 .
.
Приклад 6. В кімнаті є три вимикачі освітлення. Розробити схему, яка дає можливість здійснювати вмикання і вимикання освітлення будь-яким вимикачем незалежно від положення інших двох вимикачів. Одне положення вимикача будемо вважати нульоваим (0), а друге одиничним (1). Оскільки є три вимикачі, то схема повинна реалізувати булеву функцію від трьох аргументів. Складемо таблицю істинності цієї функції при умові, що всі три вимикачі знаходяться в стані 0. Тоді зміна положення будь-якого вимикача повинно викликати вмикання освітлення. Тобто на наборах 001, 010 і 100 функція повинна дорівнювати 1. Подальша зміна положення будь-якого вимикача повинно приводити до вимикання освітлення. Тобто на наборах 011, 101 і 110 функція повинна дорівнювати 0. Подальша зміна положення будь-якого вимикача повинно приводити до вмикання освітлення, що дає F(1,1,1)=1. Таблицю значень функції 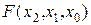 , наведено в (табл. 13).
, наведено в (табл. 13).
Представимо одержану булеву функцію у формі (1)
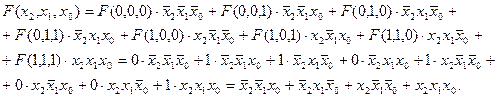
|
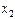 | 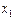 | 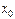 | 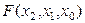 |
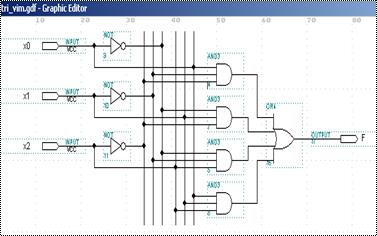
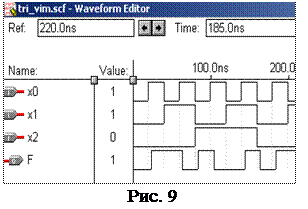 Рис. 8
Рис. 8
На рис. 8 наведено комбі-наційну схему, виконану в системі проектування MAX+plus II , яка реа-лізовує побудовану булеву функцію.
На рис. 9 наведено результати моделювання, що свідчить про правильність роботи схеми.
20. Кон’юнктивна форма – це друга відома форма представлення функцій, яка будується аналогічно до диз’юнктивної форми.
Означення 5. Логічна сума будь-якої кількості різних змінних, що входять із запереченням або без нього, називається елементарною диз’юнкцією.
Наприклад, елементарними диз’юнкціями є:
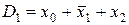 ,
, 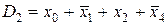 ,
, 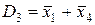 .
.
Означення 6.Кон’юнкція елементарних диз’юнкцій вигляду:
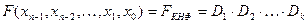 ,
,
– називається кон’юнктивною нормальною формою (КНФ).
Наприклад, функція
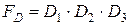 ,
,
де 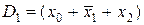 ,
, 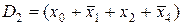 ,
, 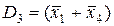 – є кон’юнктивною нормальною формою (КНФ).
– є кон’юнктивною нормальною формою (КНФ).
Означення 7. Конституентою нуля (макстермом) для функції n аргументів, називають елементарну диз’юнкцію n аргументів, яка набуває значення 0 тільки на одному наборі, а на всіх інших – значення 1.
Наприклад, набору 0110, змінних 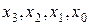 відповідає конституента нуля вигляду
відповідає конституента нуля вигляду 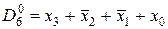 . Легко переконатись, що даний макстерм приймає значення 0 тільки на вказаному наборі, – на всіх інших наборах приймає значення 1.
. Легко переконатись, що даний макстерм приймає значення 0 тільки на вказаному наборі, – на всіх інших наборах приймає значення 1.
Означення 8. Кон’юнкція вигляду:
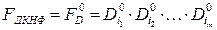 ,
,
де 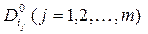 – усі конституенти нуля функції
– усі конституенти нуля функції 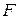 , називається досконалою кон’юнктивною нормальною формою (ДКНФ).
, називається досконалою кон’юнктивною нормальною формою (ДКНФ).
Приклад 7. Для розглянутих у прикладі 3 функцій (табл. 11) побувати ДКНФ.
Розв’язання. Маємо:
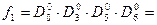
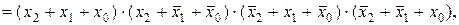
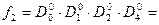
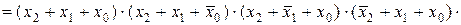
30. Досконала поліноміальна нормальна форма. Легко переконатись, що в ДДНФ можна замінити операцію диз’юнкцію на операцію додавання за модулем 2, причому рівність зберігається. Ця форма називається досконалою поліноміальною нормальною формою (ДПНФ). Для функцій з прикладу 3, маємо:
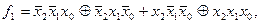
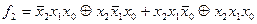 .
.
40. Канонічний поліном Жегалкіна – це поліном вигляду
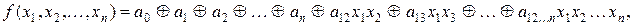 де
де 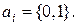
Теорема Жегалкіна. Будь-яка логічна функція може бути представлена у вигляді канонічного полінома Жегалкіна.
Приклад 8. Виразити у вигляді полінома Жегалкіна функцію 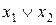 .
.
Розв’язання. Заданий вираз будемо шукати у вигляді полінома з невизначеними коефіцієнтами вигляду
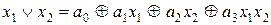 .
.
При 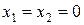 маємо
маємо 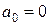 ; при
; при 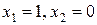 дістанемо
дістанемо 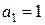 ; при
; при 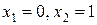 дістанемо
дістанемо 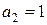 ; при
; при 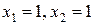 дістанемо
дістанемо 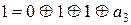 , звідки
, звідки 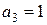 . Таким чином,
. Таким чином, 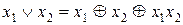 .
.
Якщо у ДПНФ усі змінні в інверсній формі замінити у відповідності з співвідношенням 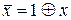 (див. аксіоми алгебри Жегалкіна), то розкривши дужки і звівши подібні члени, одержимо функцію у вигляді суперпозиції функцій з набору
(див. аксіоми алгебри Жегалкіна), то розкривши дужки і звівши подібні члени, одержимо функцію у вигляді суперпозиції функцій з набору 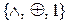 або канонічного полінома Жегалкіна.
або канонічного полінома Жегалкіна.
Приклад 9. Для розглянутих вище функцій 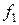 і
і 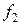 (табл. 10) побудувати канонічний поліном Жегалкіна.
(табл. 10) побудувати канонічний поліном Жегалкіна.
Розв’язання. Маємо:
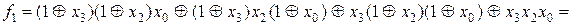
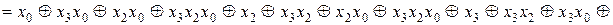
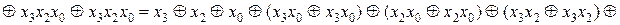
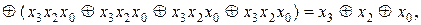
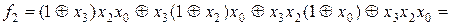
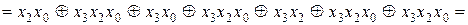
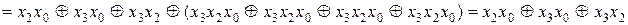 При спрощені функцій
При спрощені функцій 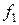 і
і 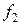 використана властивість функції додавання за модулем 2, що
використана властивість функції додавання за модулем 2, що 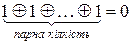 .
.