Теорема Пойнтинга
В электродинамике, как правило, принято характеризовать интенсивность процесса излучения, обусловливая особую векторную величину в каждой точке пространства, имеющую название вектора Пойнтинга П.
Смысл вектора Пойнтинга в физике заключается в том, что его направление и модуль характеризуют размер и направленность в каждой точке пространства потока энергии излучения. Вектор Пойнтинга в системе единиц СИ имеет размерность Вт/м2
При этом спад энергии, заключенного внутри воображаемого объема V с поверхностью S электромагнитного поля, определенный излучением и отнесенный к единице времени, равна
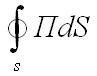
Интеграл равен величине мгновенной мощности излучения, проистекающего по направлению из объема в окружающее пространство. Если же знак представленного интеграла отрицателен, то это объясняется тем, что поток энергии излучения устремлён не из объема V, а внутрь него.
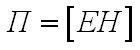
В самом деле, по теореме Остроградского – Гаусса для рассматриваемой замкнутой поверхности S будем иметь
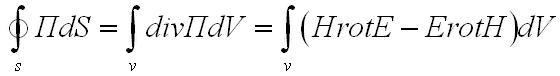
Здесь было использовано тождество векторного анализа
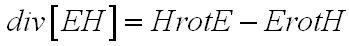
С учётом уравнений Максвелла
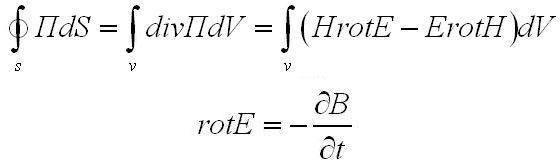 |
приобретает следующий вид
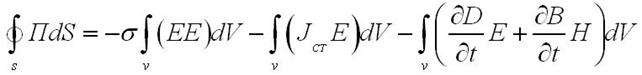
Интеграл вида
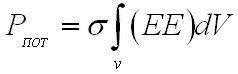
может быть именуем мгновенной мощностью потерь, будучи внутри объема V за счёт протекания токов проводимости. Иное слагаемое
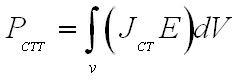
обуславливает мгновенную мощность, которая может либо отводиться из рассматриваемого объема сторонними токами, либо вноситься в него в зависимости от взаимной ориентации векторов JCTи Е. Так как
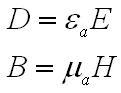
то крайний интеграл обретёт вид
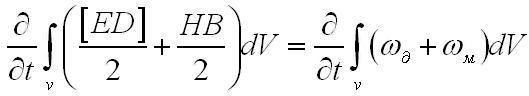
Тут мы приходим на основании вышеизложенного к интегральному соотношению вида
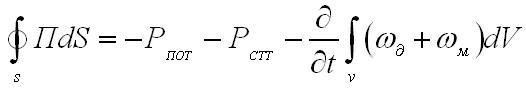
приходящемуся математическим выражением теоремы Пойнтинга. Данная теорема определяет внутри произвольной области, в которой есть электромагнитное поле, факт баланса энергий. Вектор Пойнтинга для значимого в практическом отношении частного случая, в котором поле по гармоническому закону изменяется во времени, может быть выявлен через комплексные амплитуды полей Е и Н, поскольку
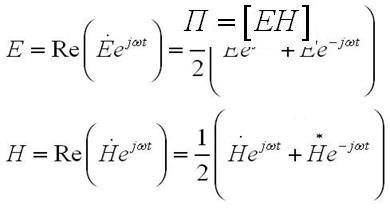 |
где* - комплексно-сопряжённые величины, подставив их в формулу П=[E*H] получим
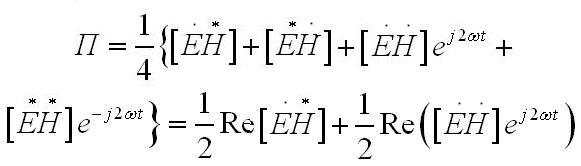
Слагаемое первое, в части формулы справа, во времени неизменно, в отличие от второго слагаемого, которое изменяется во времени с удвоенной частотой.
Тем самым в электромагнитном поле, изменяющемся во времени по гармоническому закону, ход переноса энергии характеризуется, с одной стороны вещественным вектором, равным средней за период плотности мощности излучении,
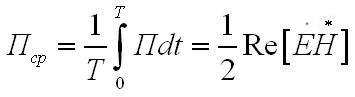
и вещественным вектором, который указывает на присутствие колеблющейся составляющей вектора Пойнтинга
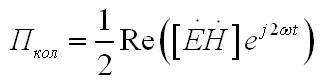
Необходимо не упускать из виду то, что среднее за период значение вектора Пкол равно нулю.
На основе уравнений Максвелла теоретическое рассмотрение и физический опыт позволяют утверждать, что термин «излучение» в узком смысле слова применим лишь к переменным во времени процессам в силу волнового характера распространения электромагнитного поля.
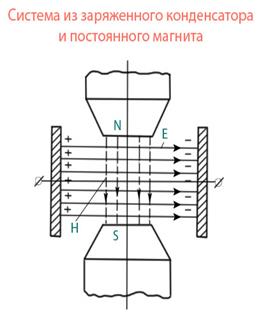 Поля Е и Н тут не параллельны друг другу, это позволит ввести отличный от нуля вектор Пойнтинга П=[ЕН] в каждой точке пространства. От того, что рассматриваемые поля статические и токи проводимости не протекают в системе, в соответствии с уравнениями Максвелла
Поля Е и Н тут не параллельны друг другу, это позволит ввести отличный от нуля вектор Пойнтинга П=[ЕН] в каждой точке пространства. От того, что рассматриваемые поля статические и токи проводимости не протекают в системе, в соответствии с уравнениями Максвелла
rotH=0 rotE=0 => divП=0
Тем самым в предоставленной физической задаче векторное поле П не обладает источниками; его поток через любую замкнутую поверхность равен нулю, это говорит о постоянстве полной энергии электромагнитного поля во времени, внутри произвольной замкнутой поверхности.
Иногда вводится комплексный вектор Пойнтинга
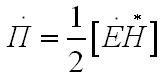 |
при анализе гармонически изменяющихся во времени электромагнитных волновых полей обладающий тем свойством, что
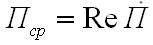
Плоские эл/м волны.
Проанализируем бескрайнее трехмерное пространство с декартовой системой координат х, у, z. У которого в каждой точке задана некоторая величина А (её физическая природа безразлична), меняющаяся в пространстве и во времени по закону
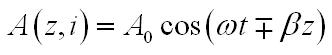
В пространстве (в предоставленном моменте) имеется монохроматическая плоская волна. Называемый фазой волны ωt-+βz – аргумент косинуса является пространственной координаты z и функцией времени t. Если же z зафиксировать, то величина А приобретает такие же значения через небольшие промежутки времени, кратные периоду T=2π/ω. Если зафиксировано время, то величина А периодически изменяется вдоль оси z с периодом λ именуемым длиной волны. Величины βи λ связаны между собой:
β=2π/λ
Число β служит значимой характеристикой волнового процесса и называется постоянной распространения волны. Также могут использоваться термины как волновое число и фазовая постоянная. Весь смысл величины β с физической стороны в том, что она указывает, на сколько радиан фаза волны изменяется в прохождении одного метра пути. Нахождение двух потенциальных знаков в формуле
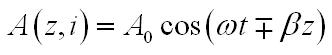
согласованно с тем, что плоские волны вполне могут исходить в двух противоположных направлениях.
Именуем поверхность, волновым фронтом плоской волны, удовлетворяющую уравнению
ωt-+βz =const
Вполне понятно, что в данном случае волновые фронты представляют собой бесконечные плоскости, перемещающиеся в пространстве со скоростью
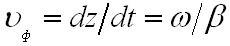
носящей название фазовой скорости и перпендикулярные оси z. От того, что время изменяется постоянно лишь в одном направлении, уравнение
ωt-βz =const
отвечает фронту волны, источающейся в направлении положительной оси z. К изменению направления её распространения ведет изменение знака в фазе волны. Подключим комплексные амплитуды плоских волн.
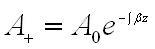
определённо для волны, подходящей в противоположную сторону
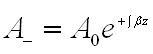
В любой реальной среде распространение волн неминуемо за счёт тепловых потерь сопровождается понижением их амплитуды. Закон затухания:
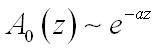
Тут α несёт название постоянной затухания волны. Введя комплексную постоянную распространения γ можно объединить величины βи α, то есть
γ=β -iα
Таким образом, вещественная часть γ находит закон изменения фазы в распространяющейся волне, в тот момент как мнимая часть характеризует затухание.
