Уравнение состояния идеального газа. Состояние газа данной массы характеризуется тремя макроскопическими параметрами: давлением p, объемом V и температурой T

Состояние газа данной массы характеризуется тремя макроскопическими параметрами: давлением p, объемом V и температурой T. Сейчас мы найдем между ними связь, а затем посмотрим, для чего эта связь нужна.
Уравнение состояния. Мы детально рассмотрели поведение идеального газа с точки зрения молекулярно-кинетической теории. Была определена зависимость давления газа от концентрации его молекул и температуры (см. формулу 9.10). На основе этой зависимости можно получить уравнение, связывающее все три макроскопических параметра p, V и T, характеризующие состояние достаточно разреженного газа данной массы. Это уравнение называют уравнением состояния идеального газа.
Подставим в уравнение p=nkT выражение для концентрации молекул газа. Учитывая формулу (8.8), концентрацию газа можно записать так:

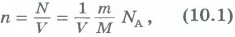
где N_A - постоянная Авогадро; m - масса газа; M - его молярная масса.
После подстановки формулы (10.1) в выражение (9.10) будем иметь

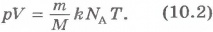
Произведение постоянной Больцмана k и постоянной Авогадро N_A называютуниверсальной (молярной) газовой постоянной и обозначают буквой R:

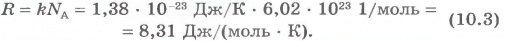
Подставляя в уравнение (10.2) вместо kN_A универсальную газовую постоянную R, получим уравнение состояния для идеального газа произвольной массы:

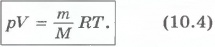
Единственная величина в этом уравнении, зависящая от рода газа, - это его молярная масса.
Из уравнения состояния вытекает связь между давлением, объемом и температурой идеального газа, который может находиться в двух любых состояниях.
Если индексом 1 обозначить параметры, относящиеся к первому состоянию, а индексом 2 - параметры, относящиеся ко второму состоянию, то согласно уравнению (10.4) для газа данной массы

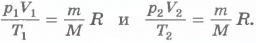
Правые части этих уравнений одинаковы, следовательно, должны быть

равны и их левые части:

Уравнение состояния в форме (10.5) называется уравнением Клапейрона и представляет собой одну из форм записи уравнения состояния. Уравнение состояния в форме (10.4) было впервые получено великим русским ученым Д. И. Менделеевым. Его называют уравнением Менделеева - Клапейрона.
Для чего нужно уравнение состояния? Не только идеальный газ, но и любая реальная система - газ, жидкость, твердое тело - характеризуется своим уравнением состояния. Но только эти уравнения намного сложнее, чем уравнение Менделеева - Клапейрона для идеального (достаточно разреженного) газа.
Знать уравнение состояния необходимо при исследовании тепловых явлений. Оно позволяет полностью или частично ответить сразу на три группы различных вопросов.
1. Уравнение состояния позволяет определить одну из величин, характеризующих состояние, например температуру, если известны две другие величины. Это и используют в термометрах.
2. Зная уравнение состояния, можно сказать, как протекают в системе различные процессы при определенных внешних условиях: например, как будет меняться давление газа, если увеличивать его объем при неизменной температуре, и т. д. Этому посвящен следующий параграф.
3. Наконец, зная уравнение состояния, можно определить, как меняется состояние системы, если она совершает работу или получает теплоту от окружающих тел. Об этом пойдет речь в конце раздела «Молекулярная физика. Тепловые явления».
Уравнение состояния не надо выводить каждый раз, его надо запомнить. Неплохо было бы помнить и значение универсальной газовой постоянной: R=8,31Дж/(моль•К).

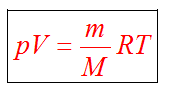
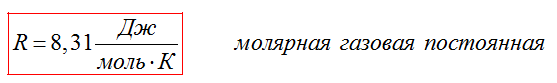
Закон Дальтона

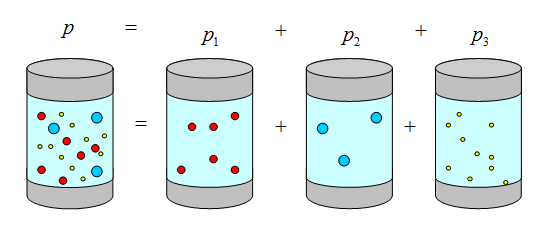
Давление смеси не взаимодействующих между собой газов равна сумме парциальных давлений каждого газа в отдельности

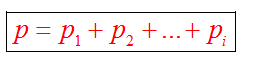
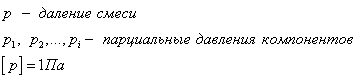
Парциальное давление - это давление компонента смеси, если бы он занимал весь предоставленный ему объем один.

Примеры решения задач:

Задача 1. Вычислить молекулярную массу бензола, зная, что масса 600 мл его паров при 87°C и давлении 83,2 кПа равна 1,30 г.

Решение. Выразив данные задачи в единицах СИ и подставив их в уравнение Клапейрона-Менделеева, находим: М = 0,0013*8,31*360/(83200*0,0006) = 0,078 кг/моль = 78 г/моль.

Задача 2. В баллоне объемом V= 10 л находится гелий под давле­нием ₁=l МПа при температуре T₁=300 К. После того как из баллона был израсходован гелий массой m=10 г,температура в баллоне понизилась до T₂=290 К. Определить давление ₂ гелия, оставшегося в баллоне.

Решение. Для решения задачи воспользуемся уравнением Клапейрона — Менделеева, применив его дважды к начальному и конечному состояниям газа. Для начального состояния уравнение имеет вид

p₁V(m₁/M)RT₁, (1) а для конечного состояния —

p₂V(m₂/M)RT₂, (2) где m₁ и m₂ — массы гелия в начальном и конечном состояниях.

Выразим массы m₁ и m₂ гелия из уравнений (1) и (2):

m₁=Mp₁V/(RT₁); (3)

m₂=Mp₂V/(RT₂); (4)

Вычитая из (3) равенство (4), получим

.

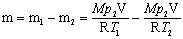Отсюда найдем искомое давление:

.

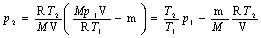Проверим, дает ли правая часть формулы (5) единицу давления. Для этого выразим все величины, входящие в нее, в соответствую­щих единицах. Единица, в которой выражается первое слагаемое, не вызывает сомнений, так как отношение T₂/T₁ — величина без­размерная. Проверим, в каких единицах выражается второе сла­гаемое:

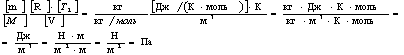
Убедившись в том, что правая часть полученной расчетной фор­мулы дает единицу искомой величины—давления, можем подста­вить в (5) значения всех величин и произвести вычисления.

В формуле (5) все величины, кроме молярной массы М гелия, известны. Найдем ее (см. пример 1). Для гелия как одноатомного газа относительная молекулярная масса равна его относительной атомной массе А_r.

Из таблицы Д. И. Менделеева найдем А_r=4. Следовательно, молярная масса гелия М= А_r10^-3 кг/моль =410^-3 кг/моль. Подставив значения величин в (5), получим

.

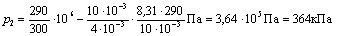Домашнее задание:

1. Е.В. Коршак, А.И. Ляшенко, В.Ф. Савченко. Физика. 10 класс, «Генеза», 2010. Читать §46 (с.150).

2. Учить лекционный материал.

3. Решить задачи № 11, 12, 14 упражнения 25.

4. Ответить на вопросы:
1. Что называют уравнением состояния?
2. Почему газовая постоянная R называется универсальной?