Центральная предельная теорема

Закон больших чисел и предельные теоремы

Под законом больших чисел в широком смысле понимают общий принцип, согласно которому совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.

Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.

Неравенство Маркова (лемма Чебышева).

Теорема 1. Если случайная величина 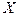принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа 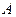верно неравенство:

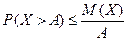
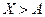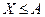Так как события и противоположные, то заменяя 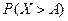выражением 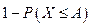, придем к другой форме неравенства Маркова:

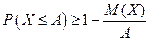
Неравенство Чебышева.

Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство Чебышева:

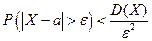, где .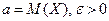

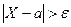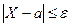Учитывая, что события и противоположны, неравенство Чебышева можно записать и в другой форме:

.

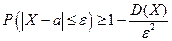Теорема Чебышева. Если дисперсии 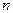независимых случайных величин 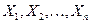ограничены одной и той же постоянной, то при неограниченном увеличении числа 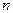средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий 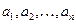, то есть

.

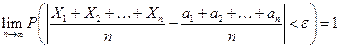При доказательстве теоремы Чебышева получена оценка

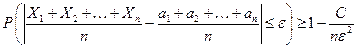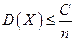( и )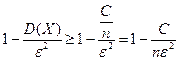

Следствие. Если независимые случайные величины 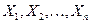имеют одинаковые математические ожидания, равные 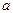, а их дисперсии ограничены одной и той же постоянной, то рассматриваемые нами неравенства примут вид:

, .

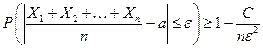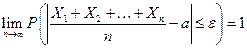Теорема Бернулли. Частость события в 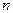повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью 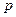, при неограниченном увеличении числа 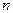сходится по вероятности к вероятности 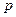этого события в отдельном испытании:

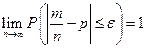
Непосредственным обобщением теоремы Бернулли является теорема Пуассона, когда вероятности события в каждом испытании различны.

Теорема Пуассона. Частость события в 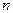повторных независимых испытаниях, в каждом из которых оно может произойти соответственно с вероятностями 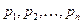, при неограниченном увеличении числа 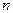сходится по вероятности к средней арифметической вероятностей события в отдельных испытаниях, то есть

.

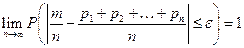Центральная предельная теорема.

Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения.

Важнейшее значение имеет теорема Ляпунова.

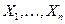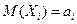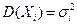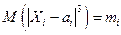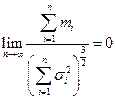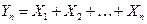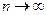Теорема Ляпунова. Если - независимые случайные величины, у каждой из которых существует математическое ожидание , дисперсия , и , то закон распределения суммы при неограниченно приближается к нормальному с математическим ожиданием 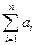и дисперсией .

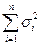ЗАДАЧИ

1. Средняя величина вклада в некоторый банк составляет 500 денежных единиц. Оцените вероятность того, что наудачу выбранный вклад не превысит 20 000 денежных единиц.
2. Математическое ожидание начальной скорости снаряда равно 600 м/сек. Оцените вероятность того, что могут наблюдаться значения начальной скорости, превышающие 900 м/сек.
3. Если среднее значение начальной скорости снаряда равно 600 м/сек, то какие значения скорости можно ожидать с вероятностью, не меньшей 0,4?
4. Средняя температура в квартире, подключенной к теплоцентрали, в период отопительного сезона составляет 20^оС, а среднее квадратическое отклонение равно 2^оС. Оцените вероятность того, что температура в квартире отклонится от средней по абсолютной величине не более чем на 5^оС.
5. Игральный кубик подбрасывается 180 раз. Используя неравенство Чебышева, оцените вероятность того, что 5 очков появится от 24 до 36 раз. Оцените вероятность этого же события с помощью интегральной теоремы Лапласа.
6. Вероятность получения с конвейера изделия высшего качества равна 0,6. Используя неравенство Чебышева и интегральную теорему Лапласа, оцените вероятность наличия от 340 до 380 изделий высшего качества в партии из 600 изделий. Сравните полученные результаты.
7. Вероятность получения с конвейера изделия высшего качества равна 0,8. Проверяется 800 изделий. Случайная величина 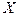- число изделий высшего качества. Укажите промежуток, в котором значения этой случайной величины можно ожидать с вероятностью, не меньшей 0,5.
8. Дисперсия каждой из независимых случайных величин 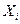, означающей продолжительность горения электролампочки, не превышает 20 час. Сколько надо взять для испытания лампочек, чтобы вероятность того, что абсолютное отклонение средней продолжительности горения лампочки от средней арифметической их математических ожиданий не превышает одного часа, была не меньше 0,95?
9. Каждая из 2000 независимых случайных величин 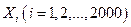имеет дисперсию, равную 4,5. Математические ожидания этих случайных величин одинаковы. Оцените вероятность того, что среднее арифметическое случайных величин отклонится от математического ожидания по абсолютной величине не более чем на 0,15.
10. Оцените вероятность того, что при 200 бросаниях монеты относительная частота появления герба отклонится от вероятности появления герба при одном испытании по абсолютной величине не более чем на 0,1.

Системы случайных величин

На практике при анализе случайных явлений приходится сталкиваться с задачами, результат которых описывается не одной случайной величиной, а системой случайных величин.