Отношение эквивалентности. Теорема о разбиении множества отношением эквивалентности на классы.
Определение 1.Бинарное отношение  на множестве А называется отношением эквивалентности,если
на множестве А называется отношением эквивалентности,если  - рефлексивно, симметрично и транзитивно.
- рефлексивно, симметрично и транзитивно.
Определение 2.Пусть  -отношение эквивалентности на множестве А. Множество
-отношение эквивалентности на множестве А. Множество 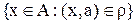 называется классом эквивалентностис представителем а или смежным классом А по
называется классом эквивалентностис представителем а или смежным классом А по  . И обозначается а\
. И обозначается а\  .
.
Множество всех классов эквивалентности называется фактор - множеством и обозначается А\  .
.
Определение 3.Пусть 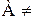 Ø. Разбиениеммножества А на классы называется совокупность его непустых подмножеств множества А, объединение которых совпадает с самим множеством А, а пересечение любых двух различных из них пусто. Другими словами совокупность из S подмножеств множества А является разбиением множества А, если выполняются следующие условия:
Ø. Разбиениеммножества А на классы называется совокупность его непустых подмножеств множества А, объединение которых совпадает с самим множеством А, а пересечение любых двух различных из них пусто. Другими словами совокупность из S подмножеств множества А является разбиением множества А, если выполняются следующие условия:
1) каждое подмножество из S непусто;
2) объединение всех подмножеств из S совпадает с самим множеством А;
3) пересечение любых двух различных подмножеств из S равно пустому множеству.
Теорема 1.Если на непустом множестве А задано отношение эквивалентности  , то А разбивается отношением
, то А разбивается отношением  на непересекающиеся классы, причем эти классы имеют вид а\
на непересекающиеся классы, причем эти классы имеют вид а\  , где
, где 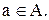
Доказательство:Пусть а\  =
= 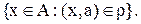 Необходимо показать, что:
Необходимо показать, что:
1) 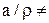 Ø.
Ø.
2) 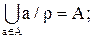
3) из 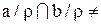 Ø следует, что
Ø следует, что 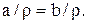
1) Действительно, так как  - отношение эквивалентности, то
- отношение эквивалентности, то  - рефлексивно, а, значит,
- рефлексивно, а, значит, 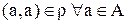 . Следовательно,
. Следовательно, 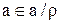 , то есть
, то есть 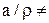 Ø.
Ø.
2) Так как 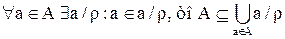 . С другой стороны,
. С другой стороны, 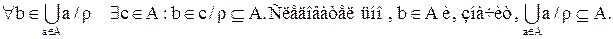
Отсюда, 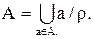
3) Предположим, что 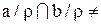 Ø. Пусть, например,
Ø. Пусть, например, 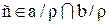 , тогда, по определению класса эквивалентности,
, тогда, по определению класса эквивалентности, 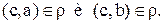
Покажем, что 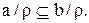 Пусть
Пусть 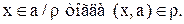 Так как в силу симметричности
Так как в силу симметричности  ,
, 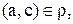 то в силу транзитивности
то в силу транзитивности  ,
, 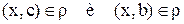 . Следовательно,
. Следовательно, 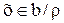 . В силу произвольности выбора х, получаем:
. В силу произвольности выбора х, получаем:
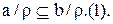
Покажем, что 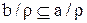 . Пусть
. Пусть 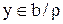 тогда
тогда 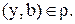 Так как
Так как 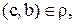 то в силу симметричности
то в силу симметричности  ,
, 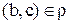 . Следовательно, с учетом транзитивности
. Следовательно, с учетом транзитивности  ,
, 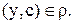
Из 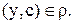 и
и 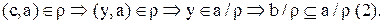
Из (1) и (2) 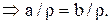 Получили противоречие с предположением, о том, что
Получили противоречие с предположением, о том, что 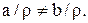
Итак, множество А является объединением непустых непересекающихся классов, вида а\  . Что и требовалось доказать.
. Что и требовалось доказать.
Замечание. Пусть  - отношение эквивалентности на непустом множестве А. Тогда по теореме 1 множество А разлагается на непересекающиеся классы эквивалентности по отношению
- отношение эквивалентности на непустом множестве А. Тогда по теореме 1 множество А разлагается на непересекающиеся классы эквивалентности по отношению  с представителем а.
с представителем а.
Пример: Дано множество: A={1,2,3,4}, на котором задано отношение эквивалентности  ={(1,1);(2,2);(3,3);(4,4);(2,4);(4,2)}. Построить разбиение множества А на непересекающиеся классы, соответствующее оношению эквивалентности
={(1,1);(2,2);(3,3);(4,4);(2,4);(4,2)}. Построить разбиение множества А на непересекающиеся классы, соответствующее оношению эквивалентности  .
.
Решение: A1={1}; A2={2,4}; A3={4}. A/  ={A1, A2, A3}.
={A1, A2, A3}.
Теорема 2.Пусть 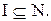 Если
Если 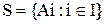 - разбиение непустого множества А на непересекающиеся классы, то S соответствует отношение эквивалентности
- разбиение непустого множества А на непересекающиеся классы, то S соответствует отношение эквивалентности 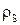 на множестве А, причем
на множестве А, причем 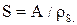
Доказательство.Пусть 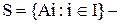 разбиение непустого множества А на непересекающиеся классы. Тогда, 1)
разбиение непустого множества А на непересекающиеся классы. Тогда, 1) 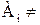 Ø,
Ø, 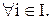 2)
2) 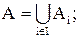
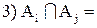 Ø
Ø 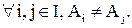
Определим на множестве А бинарное отношение 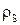 по правилу:
по правилу: 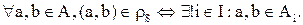 Другими словами, элементы a и b находятся в отношении
Другими словами, элементы a и b находятся в отношении 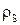 тогда и только тогда, когда они принадлежат одному и тому же классу
тогда и только тогда, когда они принадлежат одному и тому же классу 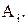
1.Так как S - разбиение А, то 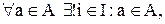 и так как элемент a принадлежит одному классу
и так как элемент a принадлежит одному классу 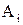 , то по определению
, то по определению 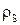 , пара
, пара 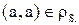 , то есть
, то есть 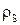 - рефлексивно на А.
- рефлексивно на А.
2.Пусть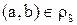 .Тогда, по определению
.Тогда, по определению 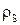 , a и b принадлежат одному и тому же классу
, a и b принадлежат одному и тому же классу 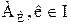 . Следовательно, и элементы b и a принадлежат одному и тому же классу
. Следовательно, и элементы b и a принадлежат одному и тому же классу 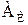 . По определению
. По определению 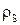 имеем:
имеем: 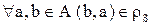 , то есть
, то есть 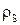 -симметрично на А.
-симметрично на А.
3.Пусть 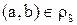 и
и 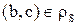 . Значит, по определению
. Значит, по определению 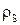 , а и b принадлежат одному и тому же классу Аt и b и с принадлежат одному и тому же классу Аk. Так как b
, а и b принадлежат одному и тому же классу Аt и b и с принадлежат одному и тому же классу Аk. Так как b 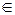 Аt и b
Аt и b 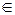 Аk, то Аt= Аk, следовательно, а и с принадлежат одному и тому же классу и, значит, (а, с)
Аk, то Аt= Аk, следовательно, а и с принадлежат одному и тому же классу и, значит, (а, с) 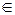
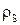 . Итак,
. Итак, 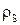 - -транзитивно на А.
- -транзитивно на А.
Следовательно, 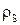 - отношение эквивалентности на А.
- отношение эквивалентности на А.
Так как каждый класс эквивалентности по отношению эквивалентности 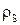 состоит из тех и только тех элементов из А, которые находятся в отношении
состоит из тех и только тех элементов из А, которые находятся в отношении 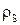 , то классы эквивалентности совпадают с классами из S. Но множество всех классов эквивалентности есть
, то классы эквивалентности совпадают с классами из S. Но множество всех классов эквивалентности есть 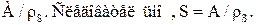 Что и требовалось доказать.
Что и требовалось доказать.
Замечание. В силу теорем 1 и 2, между множеством всех отношений эквивалентности на множестве А и множеством всех разбиений множества А на непересекающиеся классы существует взаимно однозначное соответствие. Следовательно, эквиваленций на конечном множестве А существует столько, сколько существует разбиений множества А.
Пример.Подсчитать, сколько отношений эквивалентности существует на множестве А={1,2,3}. Выписать отношения эквивалентности на А и соответствующие им разбиения.
Решение.
1.S1={{1},{2},{3}} 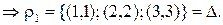
2.S2={{1,2},{3} 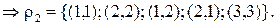
3.S3={{1,3},{2}} 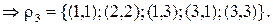 .
.
4.S4={{1},{2,3}} 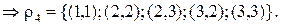 .
.
5.S5={{1,2,3}} 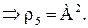
Итак, существует лишь 5 разбиений множества А, следовательно, на А существует лишь 5 отношений эквивалентности.
