Механическая система. Число степеней свободы, обобщенные координаты
В качестве элементарного материального объекта теоретической механики в ММ рассматривается материальная точка. Т. е. тело, обладающее массой, размерами которого в данной задаче можно пренебречь. Под механической системой понимается любая совокупность материальных точек, связанных или несвязанных между собой в данной задаче и в данный момент времени.
Механические системы могут состоять из раздельных (свободных) материальных точек или бесконечного множества таких точек, образующих твердое или упругое тело, а также из комбинации материальных точек твердых и упругих тел. Материальные точки и тела механической системы называют ее элементами.
Текущее положение любого деформируемого тела в пространстве при действии переменных нагрузок не может быть задано конечным числом координат, т.е. такая система имеет бесконечное число степеней свободы.
Если положение всех элементов дискретной системы в неподвижном пространстве в произвольно выбранный момент времени полностью и однозначно определяется посредством задания некоторого числа n взаимно независимых величин q1, q2, … , qn, то эти величины называют обобщенными координатами. А само число n – число степеней свободы данной механической системы.
Число степеней свободы механической системы зависит от ограничения накладываемых на перемещения элементов, которые называют связями.
Если положение всех элементов дискретной системы в неподвижном пространстве в произвольно выбранный момент времени полностью и однозначно определяется посредством задания некоторого числа n взаимно независимых величин q1, q2, … , qn, то эти величины называют обобщенными координатами. А само число n – число степеней свободы данной механической системы.
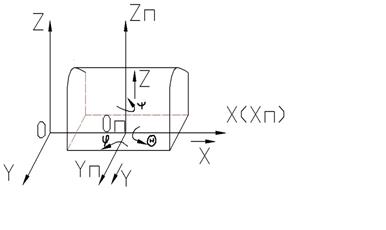
Для определения положения кузова выбрана неподвижная система прямоугольных координат OXYZ с осями, параллельными главным центральным осям вагона, установленного в середине рельсовой колеи. Относительно каждой из осей координат кузов вагона может совершать два движения – вдоль и вокруг оси, которые в общем случае являются составляющими его более сложного пространственного перемещения.
 С целью упрощения аналитических исследований указанные колебания считаются малыми. Это означает, что каждой координате, определяющей текущее отклонение вагона от равновесного положения, и всем ее производным по времени приписывается свойство понижать порядок произведений, в которые они входят в качестве сомножителя, на единицу. В результате после разложения каждого из членов уравнений движения в ряд по возрастающим степеням малых величин появляется возможность указанные уравнения упростить путем отбрасывания в них малых величин высоких порядков. При исследовании малых колебаний вагона точность составления их дифференциальных уравнений обычно ограничивается учетом слагаемых, являющихся малыми величинами первого порядка.
С целью упрощения аналитических исследований указанные колебания считаются малыми. Это означает, что каждой координате, определяющей текущее отклонение вагона от равновесного положения, и всем ее производным по времени приписывается свойство понижать порядок произведений, в которые они входят в качестве сомножителя, на единицу. В результате после разложения каждого из членов уравнений движения в ряд по возрастающим степеням малых величин появляется возможность указанные уравнения упростить путем отбрасывания в них малых величин высоких порядков. При исследовании малых колебаний вагона точность составления их дифференциальных уравнений обычно ограничивается учетом слагаемых, являющихся малыми величинами первого порядка.
При соблюдении такой степени точности оказывается, что поступательные и угловые колебательные перемещения кузова относительно осей подвижной системы координат OпXпYпZп совпадают с соответствующими перемещениями кузова вдоль и вокруг мгновенных расположений его главных осей инерции. Поэтому колебания абсолютно жесткого кузова, осуществляющиеся относительно перемещающейся вместе с поездом системы прямоугольных координат, называются его главными колебаниями.
