Типи кінцевих графів

Якщо множина вершин графа кінцева, то він називається кінцевим графом. У математику розглядаються і нескінченні графи, але ми займатися ними не будемо, тому що в практичних додатках вони зустрічаються рідко. Кінцевий граф G = (V, Е), що містить р вершин і q ребер, називається (р, q) -графом.

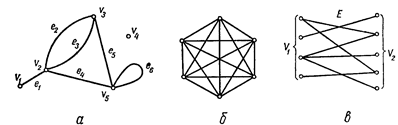
Мал. 3.3. Типи графів: а—псевдограф; б- повний граф (шестикутник); в-двочастковий граф (біграф).

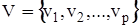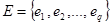Нехай і — відповідно безлічі вершин і ребер 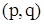- графа. Кожне ребро 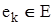з'єднує пари вершин 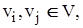які є його кінцями (граничними вершинами). Для орієнтованого ребра (дуги) розрізняють початкову вершину, з якої дуга виходить, і кінцеву вершину, у яку дуга заходить. Ребро, граничними вершинами якого є та сама вершина, називається петлею. Ребра з однаковими граничними вершинами є рівнобіжними і називаються кратними. У загальному випадку граф може містити й ізольовані вершини, що не є кінцями ребер і не зв'язані ні між собою, ні з іншими вершинами. Наприклад, для (5,6)-графа на мал. 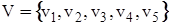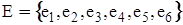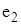3.3.,а ; ребра і 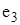рівнобіжні, ребро 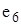є петлею, а 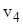— ізольована вершина.

Число ребер, зв'язаних з вершиною 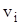, (петля враховується двічі), називають ступенем вершини і позначають через 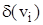чи 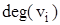. Так, для графа на мал. 9, a 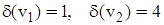і т.д. Очевидно, ступінь ізольованої вершини дорівнює нулю 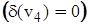. Вершина ступеня одиниці називається кінцевою чи висячою вершиною 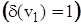. Легко показати, що в будь-якому графі сума ступенів усіх вершин дорівнює подвоєному числу ребер, а число вершин непарного ступеня завжди парне. В орграфі розрізняють позитивні 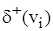і негативні 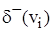ступеня вершин, що рівні відповідно числу що з 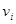і заходять у 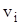, дуг. Наприклад, для вершини 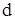орграфа (див. мал. 3.2., а) маємо 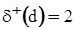і 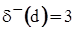. Очевидно, суми позитивних і негативних ступенів усіх вершин орграфа рівні між собою і рівні також числу всіх дуг.

Граф без петель і кратних ребер називають простим чи звичайної. Граф без петель, але з кратними ребрами називають мультиграфом. Найбільш загальний випадок графа, коли допускаються петлі і кратні ребра, називають псевдографом. Так, граф на мал. 3.1,б — це мультиграф, а на мал. 3.3,а — псевдограф. Якщо граф не має ребер 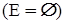, то всі його вершини ізольовані 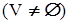, і він називається порожнім, чи нуль-графом.

Простий граф, у якому будь-які дві вершини з'єднані ребром, називається повним (на мал. 3.3,б приведений приклад повного графа із шістьма вершинами).

Якщо безліч вершин 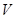простого графа допускає така розбивка на дві непересічних підмножини 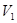і 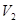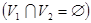, що не існує ребер, що з'єднують вершини того самого підмножини, то він називається двочастковим чи біграфом (мал. 3.3,в). Орієнтований граф вважається простим, якщо він не має строго рівнобіжних дуг і петель.

Граф, ступеня усіх вершин якого однакові і рівні 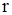, називається однорідним (регулярним) 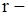го ступеня. Повний граф з 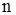вершинами завжди однорідний ступеня 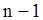, а порожній граф— однорідний ступеня 0. Граф третього ступеня називають кубічним. Він володіє поруч цікавих властивостей і, зокрема, завжди має парне число вершин.