Косвенный метод наименьших квадратов

Для оценки параметров взаимозависимых уравнений системы (4.2) используется косвенный метод наименьших квадратов, сущность которого состоит в том, что система уравнений разрешается относительно Y, так, чтобы в правых частях уравнений оставались только факторные переменные X. Затем к полученным уравнениям применяется обычный метод наименьших квадратов, и, используя полученные оценки параметров, определяют оценки исходных параметров системы.

Пусть строится простейшая система взаимозависимых уравнений вида

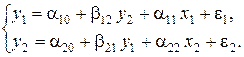(4.4)

Требуется по имеющимся данным о значениях переменных построить систему взаимозависимых уравнений регрессии вида:

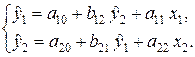(4.5)

Систему (4.5) называют структурной формой модели, а параметры a₁₀, b₁₂, a₁₁, a₂₀, b₂₁ и a₂₂ — структурными коэффициентами. Подставив правую часть второго уравнения вместо переменной 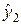в первое уравнение, после преобразований получим:

.

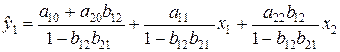(4.6)

Обозначим 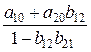как d₁₀, 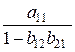как d₁₁, а 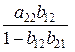как d₁₂. Тогда уравнение (4.6) примет вид:

.

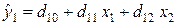(4.7)

Уравнение (4.7) называется приведенным уравнением системы взаимозависимых уравнений регрессии. Аналогичным образом, подставив правую часть первого уравнения системы (4.5) вместо переменной 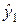во второе уравнение, и проведя преобразования, получимвторое приведенное уравнение

,

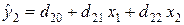(4.8)

где , , .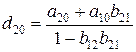

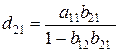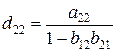Уравнения (4.7) и (4.8) образуют приведенную форму системы взаимозависимых уравнений регрессии

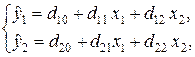(4.9)

а параметры уравнений d₁₀, d₁₁, d₁₂, d₂₀, d₂₁ и d₂₂ называются приведенными коэффициентами. Эти коэффициенты определяют обработкой исходных данных обычным методом наименьших квадратов. Структурные коэффициенты рассчитываются через приведенные по формулам, полученным обратным преобразованием системы (4.9) в (4.5):

; ; ; ; ; .

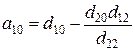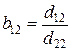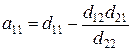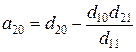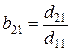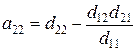(4.10)

Для того чтобы перейти от приведенной формы системы к структурной и наоборот система уравнений должна быть однозначно идентифицируема. В этом случае все ее структурные коэффициенты единственным образом определяются по коэффициентам приведенной формы системы [1, 3, 5, 8, 9, 11, 12].

Пример 4.1

Имеются значения результативных Y₁, Y₂ и факторных X₁, X₂ переменных:

Наблюдение	Y1	Y2	X1	X2
	46,5	44,5	18,2	15,2
	49,6	55,3	18,9	14,3
	65,9	62,9	13,2	22,8
	52,4	48,6	12,6	16,9
	45,6	43,2	13,2	17,6
	52,3	58,6	14,2	17,5
	50,3	55,3	17,5	14,9
	62,3	66,3	21,6	21,5
	67,6	58,9	15,2	26,3
	52,3	58,3	18,2	16,3
	56,8	62,3	13,6	22,7
	70,3	68,3	21,6	17,2

Используя косвенный метод наименьших квадратов, требуется построить систему взаимозависимых уравнений в виде:

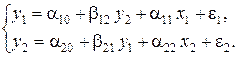
Решение

В начале строим уравнения приведенной формы системы одновременных уравнений регрессии:

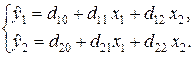
С помощью надстройки «Анализ данных… Регрессия» табличного процессора EXCEL (см. § 5.3) определяем коэффициенты приведенной формы (табл. 4.1).

Таблица	4.1
Результаты регрессионного анализа в EXCEL

Уравнение регрессии 1	Коэффициент	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	2,126	13,730	0,155	0,880
Х1	1,201	0,523	2,297	0,047
Х2	1,831	0,449	4,073	0,003
Уравнение регрессии 2	Коэффициент	Стандартная ошибка	t-статистика	P-Значение
Y-пересечение	8,424	15,529	0,542	0,601
Х1	1,449	0,591	2,451	0,037
Х2	1,319	0,508	2,595	0,029

Коэффициенты приведенной формы имеют следующие значения: d₁₀=2,126; d₁₁=1,201; d₁₂=1,831; d₂₀=8,424; d₂₁=1,449 и d₂₂=1,319, и система уравнений примет вид:

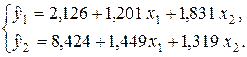
Коэффициенты структурной формы системы уравнений регрессии

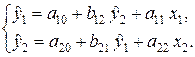
определяем по формулам:

;

;

;

;

;

.

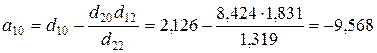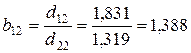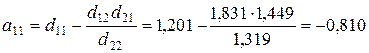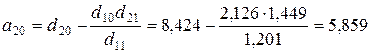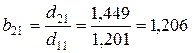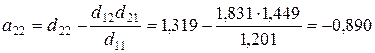Окончательно структурная форма системы примет вид:

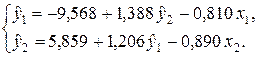
Контрольные задания

Используя ряды значений переменных, выполнить расчеты в соответствии с заданием к примеру 4.1.

Наблюдение	Ряд значений переменной
А	Б	В	Г	Д	Е	Ж	З	И	К
	28,3	36,9	18,2	33,3	37,6	34,4	35,6	32,6	14,5	42,4
	25,2	45,8	15,6	35,4	29,1	20,4	37,3	42,6	18,6	25,0
	32,1	33,4	23,6	20,1	20,3	31,3	19,6	38,6	28,9	38,2
	25,0	39,9	17,6	30,6	21,7	45,6	32,5	35,6	16,3	25,6
	18,3	41,8	14,3	47,8	42,6	24,3	28,9	39,6	15,6	26,3
	26,3	45,3	22,1	25,9	38,3	31,8	29,6	42,6	25,6	28,6
	42,5	22,8	28,9	21,7	20,3	47,6	22,3	28,6	32,6	40,7
	25,8	41,8	15,3	32,1	42,3	34,1	35,6	38,5	19,6	23,2
	29,6	31,6	26,9	38,3	37,2	25,6	34,2	34,5	29,5	52,3
	27,3	49,7	22,3	30,4	25,1	45,9	32,5	46,9	18,7	28,6
	22,1	48,5	15,6	47,2	40,8	29,1	52,1	45,7	16,3	35,6
	24,6	46,3	16,8	37,5	25,7	38,9	35,6	45,8	17,2	38,9

Каждому варианту соответствуют следующие сочетания рядов:

Вариант

Переменная

у1

у2

х1

х2

у1

у2

х1

х2

у1

у2

х1

х2

у1

у2

х1

х2

Ряд

А

Б

В

Г

Б

В

Г

Д

В

Г

Д

Е

Г

Д

Е

Ж

Вариант

Переменные

у1

у2

х1

х2

у1

у2

х1

х2

у1

у2

х1

х2

у1

у2

х1

х2

Ряд

Д

Е

Ж

З

Е

Ж

З

И

Ж

З

И

К

А

Б

Г

Д

Вариант

Переменные

у1

у2

х1

х2

у1

у2

х1

х2

у1

у2

х1

х2

у1

у2

х1

х2

Ряд

Б

В

Д

Е

В

Г

Е

Ж

Г

Д

З

И

Е

Ж

И

К

Возможны и иные сочетания рядов значений переменных.