Определение теплопроводности твердых материалов методом пластины при имитационном моделировании процесса теплообмена
Цель работы - определить теплопроводность фторопласта методом плоского слоя в зависимости от температуры, определить влияние на температурное поле внутренних источников теплоты и термических контактных сопротивлений.
Введение
Исследование явления теплопроводности может быть сведено к изучению пространственно-временных изменений величин, характеризующих теплообмен. Совокупность значений температур во всех точках какого-то тела в данный момент времени t называется температурным полем этого тела. Температурное поле в декартовой системе координат задается уравнением вида
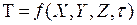 . . | 1.1 |
Совокупность точек тела, имеющих одинаковую температуру, составит изотермическую поверхность. Предел отношения изменения температуры DT к расстоянию  по нормали между соответствующими изотермическими поверхностями при
по нормали между соответствующими изотермическими поверхностями при 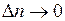 называется температурным градиентом :
называется температурным градиентом :
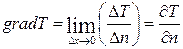 . . | 1.2 |
Количественная оценка теплоты, проходящей внутри тела вследствие теплопроводности, базируется на основном законе теплопроводности Фурье:
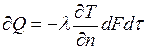 , или , или 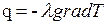 , , | 1.3 |
где величина l называется коэффициентом теплопроводности.
Для решения задач о нахождении теплопроводности обязательным является знание поля температур, то есть пространственно-временного распределения температуры в интересующей нас области. Такое распределение подчиняется основному дифференциальному уравнению теплопроводности Фурье-Кирхгофа, в основу вывода которого положен закон Фурье. Для нестационарного теплового режима в случае твердого тела с изотропными и однородными свойствами, при постоянной теплопроводности 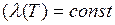 ) и при внутренних источниках теплоты уравнение Фурье-Кирхгофа для декартовой системы координат имеет вид
) и при внутренних источниках теплоты уравнение Фурье-Кирхгофа для декартовой системы координат имеет вид
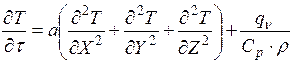 . . | 1.4 |
Здесь Т – температура [К]; t -время [с ]; a - коэффициент температуропроводности: a = lСр r, [ м2/с ]; l - теплопроводность [ Вт/(м К)]; Ср – удельная теплоемкость [ Дж/(кг К)] = 1 Дж/(кг К); r - плотность [ кг/м3]; qv – объемное тепловыделение [ Вт/м3].
Теплопроводность реальных систем, как правило, зависит от температуры и уравнение (1.4) имеет вид
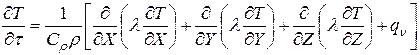 . . | 1.5 |
Для решения конкретных задач дифференциальное уравнение теплопроводности дополняется условиями однозначности. Условиями однозначности называют те дополнительные частные данные, которые характеризуют рассматриваемую задачу. Они включают в себя геометрические условия, характеризующие форму и размеры тела; физические условия, характеризующие физические свойства тела и окружающей среды; временные (начальные) условия, связанные с распределением температур в теле в начальный момент времени; граничные условия, характеризующие особенности протекания процессов теплообмена на границах тела.
Применим дифференциальное уравнение теплопроводности в сочетании с условиями однозначности к задаче об одномерном температурном поле. Рассмотрим модель плоской стенки.
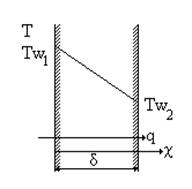 | Плоской называют стенку, толщина которой d значительно меньше двух других характерных размеров (ширины и длины). В этом случае можно пренебречь отводом теплоты через торцы стенки, считая, что тепловой поток направлен перпендикулярно большей поверхности пластины вдоль оси Х (рис.1.1). Таким образом, гео- | |
| Рис. 1.1 |
метрическими условиями однозначности заданы форма и размеры стенки. Физические условия однозначности заключаются в том, что известен материал стенки и, следовательно, известно значение теплопроводности l. Будем считать, что  материала стенки является изотропной и однородной величиной.
материала стенки является изотропной и однородной величиной.
В данной лабораторной работе временные условия однозначности определены стационарным тепловым режимом, следовательно,
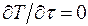 . . | 1.6 |
Сложилось три способа задания граничных условий в соответствии с тремя основными классами задач. При граничных условиях первого рода задано распределение температур на поверхности тела. В этом случае требуется определить величину плотности теплового потока. При граничных условиях второго рода известны величина плотности теплового потока и температура одной из поверхностей. И тогда возможно определить неизвестную температуру другой поверхности стенки. При граничных условиях третьего рода определяется величина плотности теплового потока, когда известны температуры сред, омывающих с разных сторон стенку, и коэффициенты теплоотдачи между поверхностями и средами. Этот случай описывает теплообмен, называемый теплопередачей.
В данной лабораторной работе будут обеспечены граничные условия первого рода. Для плоской стенки в стационарном режиме теплообмена температурное поле зависит только от одной координаты Х (рис.1.1) и тогда задача является пространственно одномерной, поскольку
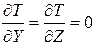 . . | 1.7 |
Дифференциальное уравнение теплопроводности (1.4) при отсутствии объемного тепловыделения и при условии постоянства теплопроводности от температуры имеет вид
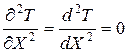 . . | 1.8 |
Закон распределения температур по толщине стенки при условии, что
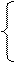 при
при 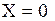
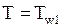 ;
;
при 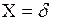
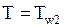 ;
;
найдется после двойного интегрирования уравнения (1.8).
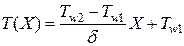 . . | 1.9 |
Величина плотности теплового потока может быть определена как
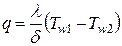 . . | 1.10 |
Отношение ld носит название тепловой проводимостью стенки, а обратная ей величина dl =R называется термическим сопротивлением стенки.
Для определения значения теплопроводности по измеренным величинам можно использовать выражение
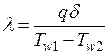 . . | 1.11 |
В этом случае полученное значение теплопроводности следует отнести к средней температуре 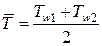 .
.
Значение теплопроводности материала определяется экспериментально в стационарных условиях. Несмотря на методическую простоту, практическое осуществление сталкивается с трудностями создания одномерного температурного поля в исследуемых образцах и учете тепловых потерь. Метод связан со значительным временем выхода установки на стационарный тепловой режим. Имитационные установки позволяют избежать этих трудностей.
При исследовании теплопроводности материалов, обладающих низкой теплопроводностью (l< 2.3 Вт/(м К)), широкое распространение получил метод неограниченного плоского слоя, когда образцу исследуемого материала придается форма тонкой круглой или квадратной пластины. При выборе геометрических размеров исследуемых образцов с низкой теплопроводностью необходимо выполнять условие 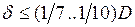 , где D – диаметр круглой пластины (или сторона квадрата), обеспечивающее одномерность температурного поля. Для устранения тепловых потерь с боковых поверхностей образца используют тепловую изоляцию или охранные электрические нагреватели. Описанный метод плоского слоя и используется в данной работе.
, где D – диаметр круглой пластины (или сторона квадрата), обеспечивающее одномерность температурного поля. Для устранения тепловых потерь с боковых поверхностей образца используют тепловую изоляцию или охранные электрические нагреватели. Описанный метод плоского слоя и используется в данной работе.
В работе требуется получить аналитическую зависимость теплопроводности от температуры l(T). Приближенно эту зависимость можно выразить в виде линейной функции
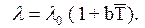 | 1.12 |
Задача состоит в определении коэффициентов l0 и b. Для их нахождения необходимы результаты обработки, как минимум, двух экспериментов с разными температурными режимами. Для определения двух неизвестных l0 и b по двум экспериментам используется система двух уравнений
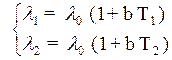 .
.
Из решения этой системы уравнений получается
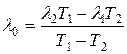 ,
,
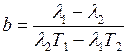 .
.
В работе проводятся три эксперимента, полученные значения l0 и b необходимо усреднить.
Порядок проведения опытов
Термопара – элемент, напряжение на котором пропорционально разности температур на ее концах.
Если две проволоки разнородных металлов спаять своими концами и включить гальванометр, то прибор не обнаружит электрического тока, когда все места соединения разнородных материалов имеют одну температуру. Если же нагреть или охладить один спай, то в цепи возникнет электрический ток, называемый термоэлектрическим током. Совокупность разнородных проволок, спаянных как указано выше, составляет так называемую термоэлектрическую пару (термопару).
Для используемых в данной работе термопар 1 вольт соответствует 16 градусам Цельсия:
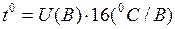 .
.
ВАРИАНТЫ
| № варианта | ||||||||
| U,B | ||||||||
| t0 | ||||||||
| t0 | ||||||||
| t0 |
После включения установки в сеть, на мониторе высвечивается тема лабораторной работы и отображается схема рабочего участка экспериментальной установки. Далее Вы вступаете в диалог с ЭВМ, в которой заложены все возможные варианты проведения эксперимента. В процессе дальнейшей работы осуществляется следующая последовательность действий.
1. Выбирается температурный режим работы установки: задается с помощью панели управления Установки. При нажатии на пиктограмму с помощью появившегося диалогового окна Вам будет предложено задать температуру горячей поверхности пластин Тг (ТГ) в пределах 45-100 С0.
2. На пульте управления последовательно включаются тумблер питания и тумблер включения нагрева.
3. Плавным вращением ручки реостата устанавливается нужное напряжение на нагревателе. Следует иметь в виду, что реостат выполнен в шаговом варианте, поэтому напряжение изменяется ступенчатым образом. Напряжение U и Тг должны находиться в соответствии друг с другом согласно графической зависимости на рисунке, на котором рабочая зона заштрихована.
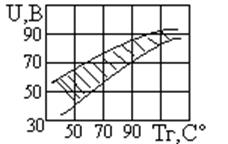 | 4. Определяются значения температур семи температурных датчиков, которые вместе со значением U заносятся в протокол эксперимента (табл.1). Регистрация показаний производится по индикаторному прибору на пульте управления, показания которого дублируются на мониторе. |
| Рис. 1.2. Рабочая зона |
5. По окончании эксперимента производится перевод всех регулирующих органов в исходное положение.
Таблица 1.1. Протокол эксперимента и результаты обработки данных
| № режима | U, В | Показания термопар | Тг | Тх | 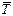 | lJ, Вт/ мС | l0, Вт/ мC | b, 1/C | ||||||
| Т1 | Т2 | Т3 | Т4 | Т5 | Т6 | Т7 | ||||||||
| С0 | С0 | С0 | С0 | С0 | С0 | С0 | С0 | С0 | С0 | |||||
Обработка результатов
1. Определяются средние температуры внутренней горячей и внешней холодной поверхностей образцов
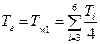 ;
; 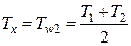 (і – номер термопары),
(і – номер термопары),
и строится графическая зависимость температуры от толщины стенки Т(х).
2. Теплопроводность фторопласта определяется на основании формулы (1.11):
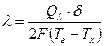 .
.
Здесь Ql - тепловой поток, прошедший через образцы за счет теплопроводности, рекомендации по расчету которого приведены ниже; F – принятая площадь поверхности одного образца ( 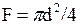 , где d = 0.14 м);
, где d = 0.14 м); 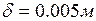 (толщина образца).
(толщина образца).
Тепловой поток Ql получается за счет вычитания из общего теплового потока Q, создаваемого нагревателем, тепловых потерь через кожух
Ql = Q – Qк;
Q = U2/R;
Qк = К (Тг –Тт).
Здесь К характеризует теплопроводность кожуха и с учетом того, что кожух имеет цилиндрическую форму можно определить его приближенное значение
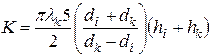 . . | 1.12 |
где R=41.0 Ом; 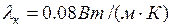 – теплопроводность материала кожуха (асбоцемента); Тт – температура наружной поверхности кожуха, определяемая 7-ой термопарой;
– теплопроводность материала кожуха (асбоцемента); Тт – температура наружной поверхности кожуха, определяемая 7-ой термопарой; 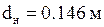 – наружный диаметр нагревателя;
– наружный диаметр нагревателя; 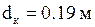 - внешний диаметр кожуха;
- внешний диаметр кожуха; 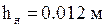 – высота нагревателя;
– высота нагревателя; 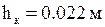 – высота кожуха.
– высота кожуха.
Значение теплопроводности l зависит от температуры материала, поэтому полученное значение l будет относиться к средней температуре исследуемого образца 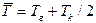 . Результаты обработки опытных данных сводятся в протокол эксперимента. Для других режимов работы установки проводятся аналогичные расчеты, в результате чего получится несколько значений lj для соответствующих средних температур
. Результаты обработки опытных данных сводятся в протокол эксперимента. Для других режимов работы установки проводятся аналогичные расчеты, в результате чего получится несколько значений lj для соответствующих средних температур 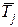 , где j – номер режима работы установки.
, где j – номер режима работы установки.
Полученные значения заносятся в таблицу 1.1.
Контрольные вопросы
1. Дайте определение температурного поля, градиента. Перечислите и дайте определения основных характеристик процесса теплообмена.
2. Основные положения, лежащие в основе вывода закона Фурье-Киргофа. Какую роль играют условия однозначности?
Работа 2 (ММТП – 011М)
