Гипербола, ее эксцентриситет, директриса и асимптоты

Определение

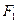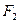Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек плоскости и , называемых фокусами, есть величина постоянная, равная 2a.

Расстояние между фокусами – 2c.

Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат (рис. 2.13.1), то каноническое уравнение гиперболы имеет вид

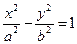(2.13.1)

Где 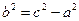. Уравнение вида (2.13.1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат – ее центром симметрии. Ось Ox называется действительной осью, а Oy – мнимой осью гиперболы. Точки пересечения гиперболы с осью называются вершинами гиперболы.

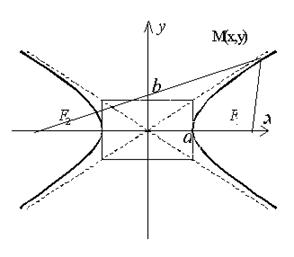
Рис. 2.13.1.

Прямоугольник со сторонами 2a и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы. Диагонали основного прямоугольника (неограниченно продолженные) являются асимптотами гиперболы и определяются уравнениями

, .

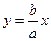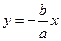(2.13.2)

Эксцентриситетом гиперболы (как и эллипса) называется число 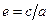, где a – расстояние от центра гиперболы до ее вершины. Очевидно, что для любой гиперболы e>1.

Если M(x;y) – произвольная точка гиперболы, то отрезк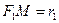и и 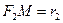называются фокальными радиусами точки М. Фокальные радиусы правой ветви гиперболы могут быть вычислены по формулам 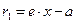и 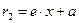. Фокальные радиусы левой ветви гиперболы – по формулам 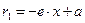и .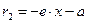

Если гипербола задана уравнением (2.13.1), то прямые, определяемые уравнениями 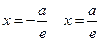, называются ее директрисами.

Пример

Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала координат, если точка 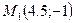лежит на гиперболе и известны уравнения асимптот .

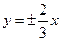Решение

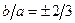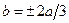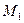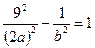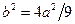Из уравнений для асимптот находим , или . Поскольку точка принадлежит гиперболе, ее координаты удовлетворяют уравнению (2.13.1): , где или 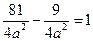. Отсюда находим 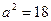, тогда 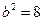, следовательно, уравнение гиперболы имеет вид .

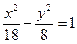Пример

Дана гипербола 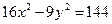. Найти ее полуоси a и b, фокусы, эксцентриситет, уравнения асимптот.

Решение

Разделим обе части этого уравнения на 144. Получим 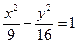. Значит a=3, b=4, следовательно оси гиперболы соответственно равны 2a=6 и 2b=8. Так как 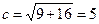, то фокусы гиперболы находятся в точках 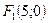и 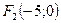. Эксцентриситет гиперболы вычисляется по формуле 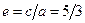. В соответствии с (2.13.2), уравнения асимптот имеют вид: .

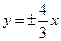Парабола, ее директриса

Определение

Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до некоторой фиксированной точки плоскости F, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно директрисе и была направлена от директрисы к фокусу. Начало координат расположим посредине между фокусом и директрисой (рис. 2.14.1). В этой системе координат данная парабола будет определяться уравнением:

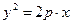(2.14.1)

где p – расстояние от фокуса до директрисы (параметр параболы). Уравнение (2.14.1) есть каноническое уравнение параболы.

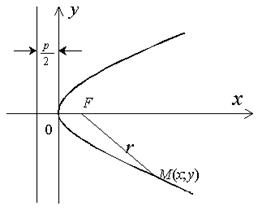
Рис. 2.14.1

Директриса данной параболы определяется уравнением 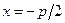. Фокальный радиус произвольной точки M(x;y) параболы может быть вычислен по формуле

.

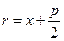(2.14.2)

Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка, в которой парабола пересекается с осью симметрии, называется вершиной параболы. При указанном выше выборе системы координат ось параболы совмещена с осью абсцисс, вершина находится в начале координат, а вся парабола лежит в правой полуплоскости.

Если вершину параболы (2.14.1) перенести в точку 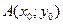, то ее каноническое уравнение примет вид .

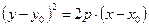Пример

Найти фокус F и уравнение директрисы параболы .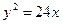

Решение

Параметр данной параболы p=12. Поскольку расстояние от фокуса до директрисы равно 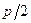, то фокус имеет координаты F(6;0), а уравнение директрисы 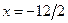, то есть x+6=0.

Пример

Составить уравнение параболы с вершиной в начале координат и фокусом в точке F(0;8).

Решение

Поскольку фокус параболы лежит на оси ординат, а ее вершина – в начале координат, то уравнение параболы можно записать в виде 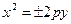. Так как ордината фокуса отрицательна, то уравнение параболы следует искать в виде .

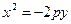Фокусное расстояние 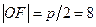, откуда 2p=32. Следовательно, уравнение параболы имеет вид .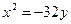