Исследование устойчивости вторым методом Ляпунова

Рассмотрим автономную систему

(4.1)
и будем исследовать устойчивость ее положения равновесия .

Определение 4.1. Положение равновесия системы (4.1) называется устойчивым по Ляпунову, если для любого можно указать такое, что:

1) если , то решение системы (4.1) определено при всех ;

2) при всех выполнено условие .

Если к тому же , то состояние равновесия асимптотически устойчиво по Ляпунову.

Пусть V(x) – функция переменной . Будем говорить, что функция V(x) положительно определена в окрестности U точки , если при и . Если же в окрестности U выполнены условия при и , то будем говорить, что функция V(x) отрицательно определена в окрестности U.

Приведенная ниже теорема А.М.Ляпунова является одной из центральных теорем так называемого второго метода Ляпунова, играющего важную роль в качественной теории дифференциальных уравнений.

Теорема 4.1.(Терема Ляпунова об устойчивости).Если в некоторой окрестностиUположения равновесия системы (4.1) существует непрерывно дифференцируемая положительно определенная функция V(x) такая, что ее производная в силу этой системы не положительна в указанной окрестности, то положение равновесия устойчиво по Ляпунову.

Теорема 4.2.(Теорема Ляпунова об асимптотической устойчивости). Пусть в некоторой окрестности U положения равновесия системы (4.1) существует непрерывно дифференцируемая положительно определенная функция V(x) такая, что ее производная в силу этой системы отрицательно определена в U. Тогда положение равновесия асимптотически устойчиво по Ляпунову.

Везде ниже, без ограничения общности, будем считать, что , т.е. 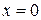– положение равновесия системы (4.1), и будем исследовать устойчивость этого положения равновесия.

Теорема 4.2 не дает оценки скорости стремления к нулю при . Следующее утверждение позволяет получить такую оценку.

Теорема 4.3.Пусть 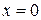положение равновесия системы (4.1) и существует положительно определенная в некоторой окрестности точки 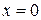функция V(x) такая, что

, (4.2)
где – некоторые положительные числа.

Тогда существует такая постоянная , что при для всех достаточно малых .

Существуют теоремы, устанавливающие условия неустойчивости положения равновесия системы (4.1). Наиболее сильной из них является теорема Четаева. Для того, чтобы сформулировать эту теорему, введем некоторые дополнительные понятия. Пусть – непрерывно дифференцируемая функция, определенная в области 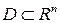, содержащей начало координат 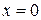. Предположим, что и что существует сколь угодно близкая к началу координат точка такая, что . Выберем так, чтобы шар содержался в и положим

. (4.3)

Множество непустое и содержится в (рис.4.1). Его границу составляют поверхность и сфера . Поскольку , начало координат лежит на границе множества .

Теорема 4.4.(теорема Четаева). Пусть 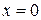– положение равновесия системы (4.1). Пусть – непрерывно дифференцируемая функция такая, что и для некоторой точки такой, что произвольно малая величина. Определим соотношением (4.3) и предположим, что в . Тогда 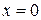– неустойчивое положение равновесия системы (4.1).

Приведем несколько примеров, иллюстрирующих применение теорем Ляпунова и Четаева.

Пример 4.1. Пусть уравнения возмущенного движения имеют вид

Здесь, очевидно, – положение равновесия. Для исследования его на устойчивость рассмотрим функцию . Производная этой функции в силу рассматриваемой системы

.
Положим . Тогда , а

Следовательно, возмущенное движение устойчиво по Ляпунову. Однако асимптотическую устойчивость мы гарантировать не можем.

Пример 4.2. Рассмотрим систему

В качестве функции Ляпунова возьмем . Имеем,

.

По теореме 4.2 состояние равновесия (0,0) асимптотически устойчиво по Ляпунову.

Пример 4.3.Рассмотрим систему

Будем искать функцию Ляпунова в виде .Тогда . Полагая , получим .

Заметим, что . Кроме того, . То есть, выполнены соотношения (4.2) с . Поэтому, согласно теореме 4.3, существует такая постоянная , что при для всех достаточно малых .

Пример 4.4.. Рассмотрим систему

Пусть . . Очевидно, в той области на плоскости , где (рис. 4.2). Значит, выполнены все условия теоремы Четаева, и состояние равновесия неустойчиво по Ляпунову.

Задание 4

Исследовать устойчивость нулевого решения, построив функцию Ляпунова и применив теоремы Ляпунова или Четаева.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.