Вопрос 21. Расчёт сложных электрических цепей методом двух узлов

Рассмотрим метод узловых напряжений (двух узлов) на примере.

Задача

Определить токи ветвей и направить их.

Порядок расчёта:

1) обозначаем узлы А и Б: под узлом А обозначаем узел, к которому направлена большая ЭДС;

2) все токи направляем к узлу А;

3) рассчитываем проводимость каждой ветви по формуле

:

4) Рассчитываем напряжение между двумя узлами по формуле:

В формулу E входит со знаком “+”, если она направлена к узлу А; если от узла — то со знаком “–”.

5) Находим токи ветвей:

6) Изменяем направление отрицательных токов.

Вопрос 22. Расчёт сложных электрических цепей методом эквивалентного генератора.

Методом эквивалентного генератора находят ток в одной ветви. Особенно удобно, если сопротивление этой ветви изменяется.

Согласно теореме об эквивалентном генераторе, любой активный двухполюсник можно заменить эквивалентной ЭДС ( ) и эквивалентным внутренним сопротивлением ( ). То, что обведено пунктиром на схеме 1, — активный двухполюсник:

Схема 1А

Схема 1Б

Чтобы найти , надо разомкнуть ветвь АБ и найти напряжение на зажимах разомкнутой ветви. Оно будет равно :

Чтобы найти , надо разомкнуть ветвь АБ, убрать все источники, оставив их внутренние сопротивления. Далее необходимо рассчитать сопротивление цепи по отношению к зажимам АБ. Это и будет .

Если известны и , то:

Задача

Дано (для схемы 1А):

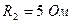
Найти ток в цепи (методом эквивалентного генератора).

Разомкнутая цепь приведена на схеме:

Находим ток холостого хода:

Найдём :

Обходим контур по второму закону Кирхгофа так, чтобы он замкнулся через напряжение (лучше взять такой контур, где меньше элементов):

Находим :

Далее можно выразить искомый ток:

Вопрос 23. Метод наложения.

Метод наложения основан на принципе наложения, согласно которому ток в каждой ветви может быть найден как алгебраическая сумма токов от действия каждой ЭДС в отдельности.

Порядок расчёта:

1) Поочерёдно оставляем в схеме по одному источнику, внутреннее сопротивление исключаемых источников также остаётся.

2) Расставляем частичные токи (обозначаем их со штрихом).

3) Находим действительный ток, как алгебраическую сумму частичных токов. Действительный ток направляем в сторону большего частичного.

Например:

Пусть , тогда .

Вопрос 24. Анализ режима работы ветви электрической цепи при изменении сопротивления этой ветви (делители напряжения Г-образный и с плавной регулировкой).

Делитель напряжения — четырёхполюсник, у которого коэффициент передачи меньше единицы ( ).

Различают Г-образный делитель напряжения и делитель напряжения с плавной регулировкой (его называют потенциометр).