Белгісізі бар сызықты теңдеулер жүйесі болғанда, мұнда , матрицалық түрде былай беріледі

Анықтауыштың екі жолының сәйкес элементтері пропорционал болса, онда оның мәні неге тең?

нөлге 0

Диагональ матрицаның анықтауышының мәні неге тең?

бас диагональ элементтерінің көбейтіндісіне

Егер анықтауышта кейбір жолдың немесе бағанның элементтерінің ортақ көбейткіші болса, онда:

оны анықтауыш таңбасының алдына шығарады

Анықтауыштың кез келген жолының немесе бағанының элементтерін бір k санына көбейткеннен:

оның мәні k есе артады

Матрицаның анықтамасы:

Элементерінің саны 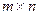-ге тең 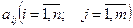элементтерінен тұратын тік кестені

Андай матрицалар тең матрицалар деп аталады?

өлшемдері бірдей және сәйкес элементтері 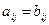болса

Андай матрица квадрат матрица деп аталады?

A) матрицаның жол саны баған санына тең болса

Бір ғана жолдан тұратын матрица қалай аталады:

жол матрица нмесе жол вектор

Матрицаларды қосу және азайту амалдары:

өлшемдері бірдей матрицалар үшін орындалады

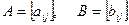
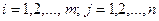матрицаларының қосындысы деп 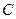матрицасын айтады, егер

элементтері 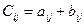болса

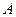матрицасын 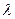санына көбейту:

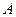матрицасының әрбір элементін 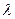санына көбейтумен мәндес

Және матрицаларын қай кезде көбейтуге болады.

бірінші матрицаның баған саны екінші матрицаның жол санына тең болса

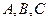үш матрицаны көбейту үшін қай теңдік орынды:

,

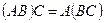Қай шарт орындалса, матрицалар алмастырылымды деп аталады: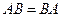

Анықтауышын есепте

-17

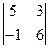анықтауышын есепте

A) 33

Кері матрица мына формуламен табылады:

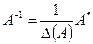
Андай матрицаның кері матрицасы болады?

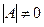болса

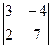анықтауышын есепте

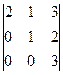анықтауышын есепте

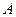матрицасының рангысының анықтамасы: осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады

Матрицаның

рангысы өзгермейді, егер:

кез келген екі жолын немесе екі бағанын ауыстырғаннан

Егер бір матрица екінші бір матрицадан элементар (жәй) түрлендіру арқылы алынса, онда ол матрицалар:

эквивалентті деп аталады.

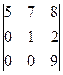анықтауышын есепте

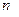белгісізді 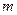сызықты алгебралық теңдеулер жүйесі үйлесімді, егер:

жүйенің негізгі матрицасының рангысы мен оның кеңейтілген матрицасының рангысына тең болса

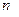белгісізді 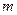сызықты алгебралық теңдеулер жүйесінің бір ғана шешімі болады, егер:

жүйенің негізгі матрицасының рангысы оның кеңейтілген матрицасының рангысына тең және ол белгісіздер саны 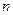-ге тең, яғни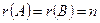

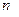белгісізді 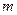біртекті сызықты алгебралық теңдеулер жүйесі:

әруақытта үйлесімді

белгісізі бар сызықты теңдеулер жүйесі болғанда, мұнда , матрицалық түрде былай беріледі.

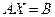
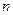белгісізді 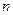сызықты теңдеулер жүйесінің матрицалық әдіспен шешкендегі матрица - шешімі 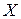былай табылады:

A)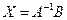

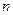белгісізді 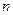сызықты алгебралық теңдеулер жүйесінің 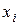шешімі 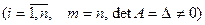Крамер формуласы бойынша былай табылады:

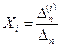
Біртекті 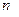белгісізді 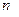сызықты теңдеулер жүйесінің бір ғана шешімі бар:

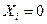, егер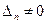

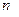белгісізді 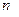біртекті теңдеулер жүйесінің шексіз көп шешімі болады, егер:

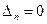
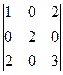анықтауышын есептеңіз:

-2

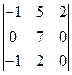анықтауышын есептеңіз:

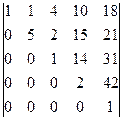анықтауышын есептеңіз:

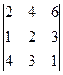анықтауышын есептеңіз:

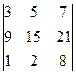анықтауышын есептеңіз:

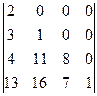анықтауышын есептеңіз:

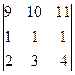анықтауышының 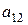элементінің минорын есептеңіз:

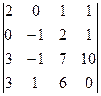анықтауышының 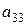элементінің минорын есептеңіз:

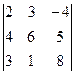анықтауышының 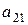элементінің минорын есептеңіз:

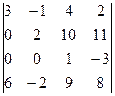анықтауышының 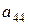элементінің минорын есептеңіз:

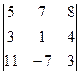анықтауышының 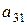элементінің 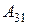алгебралық толықтауышын есептеңіз: