Центр масс

Лекция 4. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА. ЦЕНТР МАСС. УРАВНЕНИЕ ДВИЖЕНИЯ ЦЕНТРА МАСС.

Импульс

1. Одна частица (m = const)

Импульсом материальной точки (тела) называется векторная физическая величина, равная произведению массы тела на его скорость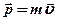

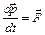
По II закону Ньютона (1) или

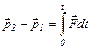- изменение импульса тела равно

Импульсу действующей силы .

Если 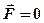, 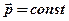(2) - закон сохранения импульса тела

1. Система материальных точек.

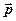- - импульс системы частиц.

По II закону Ньютона для i- той материальной точки

,

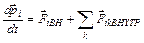Для всей системы материальных точек: 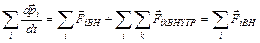(3) т.к. векторная сумма внутренних сил равна

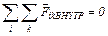
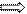Для замкнутой системы (3) 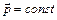(4) - импульс замкнутой системы сохраняется

Постоянным при любых взаимодействиях тел в системе.

Центр масс

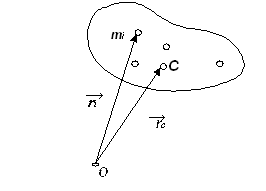Центром масс (центром инерции) системы N материальных точек m_i ( 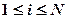), положение которых в какой-либо инерциальной системе отсчета задано радиус- векторами 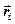( 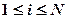), называют точку С,радиус- вектор которой определяется уравнением 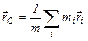(5), где m_i – масса i-той частицы, m –масса всей системы частиц.

Продифференцируем (5) по времен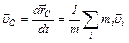и или 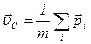(6), если скорость центра масс равна нулю 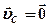, то система как целое покоится.

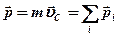Импульс системы (7) - продифференцируем по t:

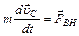(8)- уравнение движения любой системы материальных точек.

Если система отсчета связана с центром масс, 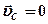и из (7)

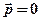- импульс системы относительно центра масс равен нулю.