Металдар мен қорытпалардың илемділігі

Металдың макроқираусыз калдықпен деформациялау қасиеті илемділік деп аталады.

Илемділіктің сандық өлшеміне қирау уақытысындағы ығысу дәрежесі жатады. Суықтай деформациялау процесі үшін осы мөлшер былай анықталады: ,

мұндағы Н – ығысу деформациясы жылдамдығының қарқындылығы. Осы мөлшер мынандай формуламен анықталады

;

; i, j = 1, 2, 3; υ_i – жылдамдық векторының сыңарлары.

Н мөлшері материалды нүктенің қозғалу траекториясы бойымен анықталады.

Барлық болып өткен деформациялау тарихындағы жинаған деформацияны Λ_р илемділіктің шегі деп атайды.

Монотонды деформация үшін Λ_р мөлшері логарифмдік деформацияның қарқындылығы мөлшерімен тең болып келеді. Логарифмдік деформацияның қарқындылығы мынандай формуламен анықталады:

,

мұндағы (k = 1, 2, 3) – қирау уақытысындағы басты логарифмді деформация.

Илемділіктің шегі көп факторлардың күрделі функциясы болып есептеледі және мынандай факторлардан тәуелді болады: металдың химиялық құрамы мен құрылымы; деформациялаудың температура-жылдамдық жағдайы; кернеулік күй; қирауға дейінгі болып өткен кернеу мен деформацияның уақыт бойынша даму тарихы; геометриялық факторлар және сыртқы орта.

Илемді деформация кезінде дислокацияларды жинау, демек микросынықтарды жинау жүреді. Осы микросынықтарды жинаумен бірге, олардың жазылу мүмкіндігі бар болады. Микросынықтардың жазылуы үш осьті созудан үш осьті қысуға өткен кезде, яғни қатаңдық коэффициенті азайған кезде көбейеді. Қатаңдық коэффициенті кернеу күйінің сұлбасын санды сипаттайды. Осы коэффициент мынандай формуламен анықталады:

,

мұндағы σ – орташа кернеу; Т – жанама кернеудің қарқындылығы.

Суықтай деформациялаған кезде ығысу деформациясының шегі Λ_р (материалды қирауға алып келетін ығысу деформациясының дәрежесі) және кернеу күйі сұлбасының көрсеткіші арасында бір мағаналы байланыс бар (оқулық [4] қараңыз).

Мынандай формуламен анықталатын интегралды:

илемділіктің қорын қолданудың дәрежесі деп атайды. Осы формуланы суықтай деформациялаған кезде қолданады. Қирау уақытысында ψ = 1.

Шегіне жеткен қопсыту уақытысында және межелік өлшемі бар сынықтың құрылу басында, материалды нүктенің айналасындағы элементарлы көлем ұшырайтын ығысу деформациясының дәрежесі Λ_р тең болады. Металдың ақаулығының өсуі dψ₁ деформацияның қосымша өсірілуі dΛ = Нdτ көп болған сайын және Λ_р мөлшері аз болған сайын үлкен болады. Сондықтан , мұндағы С₁ – илемді қопсытудың қарқындылығын немесе ақаулықтың өсуінің қарқындылығын сипаттайтын коэффициент.

Суықтай деформациялау кезінде ақаулардың жазылу мүмкіндігі бар (кеуек, борпылдақ, микросынық сияқты ақаулар жазылуы мүмкін). Осындай жазылу деформацияның дәрежесі үлкен болған сайын нәтижелі болады және металдың илемділік шегі жоғары болған сайын, яғни Λ_р үлкен болған сайын жазылу баяу жүреді. Сондықтан қосымша өсу түрінде ақуланудың азаюын мынандай түрде жазуға болады: .

Қорытындылық нәтижені былай жазуға болады:

Бірақта С₂ = С₂(k_σ), өйткені гидростатикалық қысым жоғары болған сайын жазылу нәтижелі болады.

Н = Н (τ), яғни ығысу деформациясы жылдамдылығының қарқындылығы уақыт бойынша өзгеретіндігін, ал Λ_р = Λ_р(k_σ) және k_σ = k_σ(τ) екендігін ескеріп жоғарыда жазылған формуланы былай жазуға болады:

.

Ыстықтай илемді деформациялаған кезде рекристаллизация және диффузиялық процестер есебінен ақаулардың жазылуы жүреді. Осымен байланысты t уақтысы τ-дан алыс тұрған сайын dψ мөлшері үдемелі азайады. Н = const және Т/Т_б = θ = const болған кезде, осы азаюды мұрагерлік функциямен Е(t – τ) ескеруге болады. Осы функция толық суық деформация үшін 1-ден толық ыстық деформация болған кезде 0-ге дейін өзгереді. Мұрагерлік функциясын ескеріп жоғарыда жазылған формулаланы былай қайта жазуға болады: .

Осындай жазудың мақсаты ыстықтай деформациялаған кезде илемділіктің шегіне анықтама беру болды. Ыстықтай деформациялаған кезде илемділіктің шегінің түрі мынандай болады: , мұндағы Е(t – τ) = 0 болған кезде Λ_р = ∞. Осы беріксіздену процестері толық жүрген кезде шексіз үлкен илемді деформацияға сәйкес келеді.

Жоғарыдағы теңдіктерді интегралдап, суықтай деформациялау үшін илемділіктің қорын қолданудың дәрежесі мөлшерін ψ және қираусыз деформациялау шартын аламыз. Ол мынандай шарт: .

Ыстықтай деформациялау үшін илемділіктің қорын қолданудың дәрежесі мынандай формуламен анықталады: .

Жоғарыдағы теңдеулерге кіретін Λ_р мөлшері термомеханикалық параметрлердің функциясы болып саналады. Белгілі бір құрылымы бар әр бір қорытпа үшін, осы функцияны арнайы сынау машиналарында үлгілікті ұяқалып арқылы сығымдау немесе бұрау, созу, шөктіру сияқты сынауларын жүргізумен тәжірибе бойынша табады. Осындай сынаулардың ерекше өзгешіліктері болып сынау бөлмешігінде орта қысымын 0,1-ден 1000 МПа дейін ұстап тұру мүмкіншілігі және температураны 20 ^оС-тан 1250 ^оС дейн тұрақты ғып ұстау есептеледі.

Цилиндрлік үлгілікті созған кезде ығысу деформациясының дәрежесін (қирауға дейінгі) аяққы пішін өзгеру бойынша мынандай формуламен санауға болады:

,

мұндағы d₀ және d_p – деформацияға дейінгі және қирау уақытысындағы үлгіліктің диаметрі.

Лоде көрсеткіші мынаған тең , өйткені x_rr = x_jj . көрсеткішінің мәні сынау бөлімшегіндегі гидрастатикалық қысымнан тәуелді болады, сондықтан осы көрсеткіш мынандай формуламен анықталады:

мұндағы d – үлгіліктің ең кіші қимасындағы диаметрдің мәні;

R – созудың кейбір уақытындағы үлгіліктің мойынағы қарамының радиусы.

Сынау процесінде деформация кедергісі σ_s және үлгіліктің мойынағының параметрі d/R өзгеретін болғандықтан мөлшерін тұрақты етіп ұстау үшін сынау бөлімшегіндегі қысым Р-ны мынандай белгілі бір заңмен реттейді:

.

Енінің қалындыққа қатнасы 0,1 болатын жазық үлгілікті созған кезде, мойынақта деформация шоғырланғаннан кейін деформацияланған күй жазыққа жақын, ал деформация монотонды болады. Үлгіліктің түпкі пішін өзгертуі бойынша ығысу деформациясының дәрежесін (қирауға дейінгі) мынандай формуламен есептеуге болады:

мұндағы h₀ және h_p – қирау уақытысында және деформацияға дейінгі үлгіліктің қалыңдығы.

Жазық деформация күйі үшін x₂₂ = 0, сондықтан Лоде көрсеткіші m_s = 0. Кернеу күйінің көрсеткішін мынандай формуламен анықтайды:

Егер h/2R(L) және s_s(L) тәуелділіктері белгілі болса, = тұрақты етіп ұстау үшін сынау бөлімшегіндегі қысымды Р реттейтін заңды анықтау қиын емес. Реттейтін заң мынандай: .

Цилиндрлік үлгілікті бұраған кезде таза ығысу деформация күйі пайда болады. Лоде көрсеткіші m_s = 0. Кернеу күйінің көрсеткіші мынандай формуламен анықталады:

.

Бұраған кезде үлгіліктің осінде ығысу деформациясының дәрежесі нөльге тең, ал осы үлгіліктің бетіндегі Λ-нің мөлшері ең үлкен болады. Егер цилиндрлік үлгіліктің бетіне бойлық сызық ізді түсірсе, онда бұраған кезде осы сызықіз құрастырушыға φ еңкіш бұрышы бар бұрандалы сызық жайын алады. Қираған жерде φ_р бұрышын өлшейді, содан кейін ығысу деформациясының дәрежесін мынандай формуламен есептейді: .

Басты кернеулер σ₁ = τ_s, σ₂ = 0 және σ₃ = - τ_s болғандықтан орташа кернеу σ_о = 0 және k_σ = σ/Т = 0. Жанама кернеудің қарқындылығы Т = τ_s. Егер бұрайтын үлгілікті Р қысымымен толтырылған сұйығы бар ыдысқа орналастырса, онда σ₁ = τ_s - Р, σ₂ = - Р және σ₃ = - τ_s – Р және Т = τ_s, ал σ_о = -Р. Демек, k_σ = σ/Т = - Р/ τ_s. Сұйықтың қысымын реттей отырып әр түрлі k_σ қолданып көп тәжірибені жүргізуге болатындығы жоғарғы мәліметтен көрініп тұр. Тәжірибе кезінде металл беріктенеді. Сондықтан қысымды бір қалыпты өзгертіп k_σ = σ/Т = - Р/ τ_s тұрақты етіп ұстауға болады. Сол себептен сынау машинасын, материалдың беріктену заңына сәйкесті тәжірибенің жүрісі бойынша Р қысымды бағдарлы жоғарлату үшін арнайы электронды аппаратпен жабдықтайды.

Негізгі әдебиеттер: [1] (тарау 7, бет 176 – 194); [2] (тарау 3, бет 77 – 101); [3] (тарау 1, бет 16 – 75).

Қосымша әдебиеттер: [6] (тарау 7, бет 162 – 191).

Бақылау сұрақтары:

1. Симметриялық осі бар кернеу күйін қараған кезде қандай координатты қолданады?

2. Симметриялы осі бар кернеу күйі үшін кернеу тензорын қалай жазады?

3. Симметриялық осі бар кернеу күйі үшін цилиндрлік координаттағы тепе-теңдіктің дифференциальдық теңдеуі қандай формулалармен анықталады?

4. Симметриялық осі бар кернеу күйі үшін сфералық координаттағы тепе-теңдіктің дифференциальды теңдігі қандай формулалармен анықталады?

5. Қатаңдық коэффициенті дегеніміз не?

6. Илемділіктің қорын қолданудың дәрежесі дегеніміз не?

7. Суықтай деформациялау үшін илемділіктің қорын қолданудың дәрежесі қалай анықталады?

8. Ыстықтай деформациялау үшін илемділіктің қорын қолданудың дәрежесі қалай анықталады?

9. Илемділік диаграммасын қалай тұрғызады және қалай қолданады?

№15 дәріс. Жұмыс әдістемесі. Вариациялық әдістемесі. Илемділік деформацияға металдардың кедергісі әдістемесі.

Жұмыс әдісі илемді деформация кезінде сыртқы күштің жұмысы ішкі кедергілердің жұмыстарының қосындысына тең деген ой желіске негізделген. Илемді деформация кезінде, дененің беріктік қасиетімен анықталатын ішкі кедергілерді және сыртқы үйкеліс күшін жеңу үшін жұмысты жұмсау керек. Деформацияның жұмысы машинамен дамытылатын белсенді күштің жұмысы мен сыртқы үйкеліс күш айырмасына тең болады, яғни

немесе

(15.1)

мұндағы – белсенді күштің жұмысы; – үйкеліс күшінің жұмысы; – ішкі кедергінің жұмысы, деформацияның жұмысы.

Кіші деформация жүрген кездегі ішкі күш жұмысының өсуін анықтайық. Серпімді деформация кезінде жұмысты анықтау үшін кернеу құраушылары мен деформация құраушыларын көбейтеді, осы көбейтінділерді қосады, содан соң алынған мөлшердің жартысын табады, яғни

. (15.2)

Кернеу нөльден аяққы мәнге дейін сызықты өсетін болғандықтан 0,5 коэффициентті қабылданған.

Илемді деформация кезінде бастапқы кернеулер нөльден айырмашылықта болады және дененің пішіні шамалы өзгергенде, оларды тұрақты етіп қабылдауға болады.

Сондықтан илемді деформация кезінде жұмыстың өсуін жоғарыда жазылған формуламен анықтауға болады, бірақта 0,5 коэффициенттінсіз, яғни:

(15.3)

Осы формулаға деформация тензорының сыңарларын қойып

; ; ; ; ; .

мынандай теңдеуді аламыз:

(15.4)

Квадратты жақша ішіндегі формула мынандай формуламен анықталатын:

екі еселенген кернеу қарқындылығының екінші дәрежесіне тең.

Мынандай теңдеуді қолданып , илемділік модулінің екінші түрін илемділік модулінің бірінші түрімен ауыстырайық. Содан кейін мынандай теңдеуге сәйкесті илемділік модулінің бірінші түрін кернеу мен деформация қарқындылығы арқылы бейнелейік. Сонда мынаны аламыз

.

(15.4) формуласындағы квадратты жақшадағы формуланың орнына 2 және мәнінің орнына қойсақ мынаны аламыз:

. (15.5)

Соңғы формуладан мынау шығады:

. (15.6)

Жанама үйкеліс күшінің жұмысын қосып сыртқы (беткі) күш жұмысын былай бейнелеуге болады:

, (15.7)

мұндағы 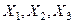– координат осьтеріне күштің проекциясы;

– координаттарға сәйкесті болатын орын ауыстыру.

Жалпы жағдайда жанама үйкеліс күшінің жұмысын былай көрсетуге болады:

, (15.8)

мұндағы – үйкеліс кернеуі (интегралдан шығарылған, өйткені тұрақты және изотропты екіндігі қабылданған).

(15.6) және (15.8) формуларды (15.1) теңдеуге қойып және абсолюттік мөлшерін қолданып мынаны аламыз:

. (15.9)

Көп жағдайларда белсенді күштің жұмысын, толық күшті сайманның қозғалысына (жаншуға) көбейту арқылы табуға болады, яғни .

Сонда толық күш мынаған тең:

. (15.10)

Есеп. Жұмыс әдістемесін ені 2b, биіктігі 2h және ұзындығы l болатын жолақты шөктіргенде күшті анықтау үшін қолданайық. Деформация жазық деп санау үшін жолақтың ұзындығы, оның енінен едәуір үлкен болсын. Жуықты тепе-теңдік және илемділік теңдеулерін біріктіріп шешу әдістемесінде қаралған мысалдан деформациялаудың шартын алайық. Жанасу бетіндегі үйкеліс кернеуін (τ_к) х₁ координатасынан тәуелді емес және тұрақты ғып қабылдаймыз. Жанасу бетіндегі үйкеліс деформацияны біркелкі емес таралуға алып келсе де, осы деформацияны біркелкі деп санаймыз. Кернеулер σ₁₁ және σ₃₃ осы жағдайда басты кернеулер болады. Илемділік шартына сәйкесті мынаны жазуға болады: σ_i = σ_т(σ_s).

Кішкентай шөктіру кезінде х₃ осі бойымен салыстырмалы деформация теріс таңбамен алынған салыстырмалы жаншуға тең, яғни

; ; .

Осындайда (8.22) формуласына сәйкесті деформацияның қарқындылығы былай анықталады:

.

Интегралдаған кезде жолақ қимасының бірден төрт шегінде l өлшемінің тұрақтылығын ескеріп, (15.1) формуласына сәйкесті ішкі күштің абсолюттік жұмысын мынандай теңдеумен анықтаймыз:

.

Жазық деформация жағдайында жанасу бетімен сырғу тек х₁ осі және екі жанасу бетімен жүретін болғандықтан, (15.8) формуласына сәйкесті үйкеліс күші жұмысын былай анықтаймыз: .

Орын ауыстыруды былай табамыз (оқулық [4] қараңыз): и₁ = ε₁ + С.

Интегралдау тұрақтысы (ол х₃ осінен тәуелді емес) х₁ = 0 және и₁ = 0 болған кезде мынаған тең: С = 0.

Бұрынғы теңдеуге и₁-дің мәнін қойып мынаны аламыз:

Алынған А_Д және А_ТР мәндерін (15.10) теңдеуіне қойып мынаны аламыз:

.

Осы теңдеуді жанасу ауданына 2bl меньшікті қысымды былай анықтаймыз:

.

Мынаны қабылдап: жуықты тепе-теңдік және илемділік теңдеулерін біріктіріп шешу әдістемесімен шығарылған формуланы аламыз (оқулық [4] қараңыз).

Көптеген жағдайда жұмыс әдістемесімен толық және меньшікті күшті едәуір оңай анықтауға болады. Жоғарыда келтірілген жазық деформация жағдайында жолақты шөктіру мысалы үшін, оны келесі жолмен іске асыруға болады.

Ішкі кедергі жұмысы және үйкеліс күшін ескермейтін деформацияның жұмысы, деформацияның кедергісін жанасу ауданына және абсолюттік жаншуға көбейтумен табады, яғни .

Үйкеліс күшінің жұмысын, үйкеліс күшін сайманның жанасу беті бойымен металдың орын ауыстыруына көбейтіп анықтайды.

Үйкеліс күшін Т үйкеліс кернеуі тұрақты және тең деген шартты орындай отырып табамыз, яғни .

Сайман бойымен металдың орын ауыстыруы мынаған тең: и₁ = ε₁₁х₁.

Бірақта деформация жазық болған кезде мынандай шарт орындалады: .

Демек, орын ауыстыру мынаған тең: .

Жолақтың енінің ортасында нөльге және х₁ = b болған кезде осы жолақтың шетінде ең үлкен мәнге жетіп орын ауыстыру (и₁) х₁-тен сызықты тәуелді болады, яғни .

Орын ауыстырудың орташа мәні мынаған тең: .

Екі жанасу беті бойынша үйкеліс күшінің жұмысы мынаған тең: .

Толық меншікті күшті сәйкесті былай анықтаймыз:

; .