Предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному давлению

Предельное сопротивление сдвигу связных грунтов при завершенной их консолидации есть функция первой степени от нормального давления (сжимающего напряжения)

15.Недоуплотненные грунты – грунты, у которых при незавершенной консолидации образовались структурные связи, препятствующие их дальнейшему уплотнению. Просадки – местные, быстро протекающие осадки недоуплотненных структурно-неустойчивых грунтов, обусловленные резким изменением их структуры, сопровождаются выдавливанием текучепластичных масс в сторону от местного воздействия. Грунты с такими свойствами – просадочные. Это лессовые грунты при замачивании под нагрузкой, сильнольдистые мерзлые и вечномерзлые при оттаивании; органо – минеральные илы при быстром нагружении; рыхлые слабые пески – при воздействии вибраций.

Просадочность грунтов оценивается относительной просадочностью:

,

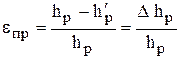где h_p – высота образца ненарушенной структуры; h¢_p – его же высота, при воздействии р > р_стр

e_пр ³ 0,02 – просадочные

При р = 0,2 – 0,25 МПа для лессовых при замачивании и р = 0,25 – 0,4 МПа мерзлые и вечномерзлые при оттаивании:

e_пр = А_о + m_dр,

где А_о – коэф-т просадки лессовых и коэф-т оттаивания мерзлых и вечномерзлых грунтов; m_d - угловой коэф-т прямой, характеризующий относит. сжимаемость в процессе просадки.

14.Многочисленные исследования показывают, что зависимость между напряжениями и деформациями нелинейна, и в общем виде ее можно записать как

e = a_c s_c+ a _n(s_n -s_c)^m, (2.61)

где a_c и a_n – коэффициенты, определяемые опытом; s_c – напряжение, не превышающее структурной прочности грунта s_c£P_стр; s_n – напряжения, обусловливающие деформации грунта, s_n­-s_c=s; m – параметр нелинейности, определяемый опытным путем.

Коэффициент a_c обратно пропорционален модулю упругости:

.

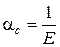Коэффициент a_n зависит от модуля общей деформации E₀:

,

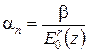где b – коэффициент, зависящий от коэффициента Пуассона; r – параметр, меньший или равный единице, определяется также опытным путем.

При давлениях больше структурной прочности формулу (2.60) можно записать так:

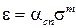, (2.62)

где a_cn – общий коэффициент пропорциональности,

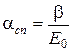
Фаза уплотнения соответствует уровням напряжений в грунте, в диапазоне которых процесс его деформирования удовлетворительно подчиняется закону уплотнения Терцаги. Линейная зависимость между деформациями и напряжениями в этой фазе не является обратимой. При разгрузке штампа из диапазона давлений, соответствующего фазе уплотнения, грунт деформируется по линейной зависимости, не совпадающей с ветвью нагрузки. При полной разгрузке штампа (рис. 1.5) имеет место необратимая (пластическая) осадка, соответствующая нулевым напряжениям по подошве. Повторное нагружение штампа до уровня напряжений, достигнутых перед разгрузкой, происходит по графику, совпадающему с графиком разгрузки. Нагружение выше этого уровня происходит по закону первичной нагрузки. Таким образом, закон уплотнения Терцаги устанавливает линейную зависимость между напряжением и суммой упругой и пластической деформации грунта. Указанная особенность закона уплотнения формулируется как принцип линейной деформируемости: при простом нагружении грунта в фазе его уплотнения сумма упругой и пластической деформации линейно зависит от действующего напряжения. Коэффициентом пропорциональности в этой линейной зависимости является модуль деформации грунта Е, названный так в отличие от модуля упругости, характеризующего деформацию упругого тела. Модуль упругости грунта Е_е определяется по графику разгрузки и является коэффициентом пропорциональности между упругой деформацией грунта и действующим напряжением. Модуль деформации используется в статических расчетах, а модуль упругости – в динамических расчетах грунтовых оснований.

Фаза сдвигов характеризует начало образования в грунте зон предельного равновесия. Зоной предельного равновесия в грунте называют геометрическое место точек, в которых не удовлетворяются условия прочности Кулона – Мора. Первоначально эти зоны образуются по краям штампа, где имеет место концентрация напряжений. Разрушение грунта сопровождается большими сдвиговыми деформациями, что нашло отражение в названии рассматриваемой фазы напряженно-деформированного состояния грунта. Уплотнение грунта в этой фазе практически не происходит. Грунт считается несжимаемым, а коэффициент Пуассона в этой фазе близок к 0,5. Давление на грунт, соответствующее началу фазы сдвигов, называют начальным критическим давлением –^нач.р_кр.

Фаза выпора является следствием развития фазы сдвигов в области грунтового массива, являющегося основанием штампа, с образованием поверхностей скольжения, отделяющих основание штампа от нижележащего грунтового массива. В результате этого осадки штампа происходят без увеличения нагрузки за счет перемещения грунта основания из-под штампа по плоскостям скольжения с выходом на поверхность грунтового массива. При этом вокруг штампа происходит поднятие (выпор) грунта, что нашло отражение в названии этой фазы. Непосредственно под штампом в фазе выпора образуется коническая переуплотненная зона, называемая ядром жесткости. Прочность этой зоны обусловлена боковыми давлениями со стороны окружающего грунта, находящегося в состоянии пластического течения. Как известно, коэффициент бокового давления в грунте в состоянии пластического течения стремится к единице. Таким образом, жесткое ядро находится до исчерпания несущей способности основания в состоянии компрессионного сжатия, близкого к трехосному сжатию, что и определяет его высокую прочность. В зонах пластического течения недоуплотненные грунты получают дополнительное уплотнение, а переуплотненные – разуплотняются. Это явление называется дилатансией. Давление, при котором наступает фаза выпора, называется предельным критическим давлением – ^пред.р_кр.

16.Лессовые породы представлены суглинками, реже—супесями. Среди них различают лесс (первичное образование) и лессовидные суглинки (переотложенные первичные образования). Гранулометрический состав их нередко бывает сходным, поэтому в строительном целесообразно пользоваться единым названием "лессовые грунты" подразделяя их по гранулометрическому составу на супеси, суглинки, глины. Для лессов типична однородность. Лессовидные суглинки обычно слоисты и могут содержать обломки различных пород. Лессовые грунты бывают палевой, палево-желтой или желто-бурой окраски. Для них характерны следующие особенности: способность сохранять вертикальные откосы в сухом состоянии, быстро размокать в воде, высокая пылеватость (содержание фракции 0,05—0,005 мм более 50% при небольшом количестве глинистых частиц), невысокая природная влажность (до 15—17%); пористая структура (более 40%) с сетью крупных и мелких пор, высокая карбонатность, засоление легко водорастворимыми солями. Просадка проявляется уже как дополнительное к осадке уплотнение. Таким образом, деформация породы складывается из «осадки — просадки». Для конкретных условий эта величина обычно постоянная. Соотношение между осадкой и просадкой может меняться. В более сухих грунтах осадка будет уменьшаться, а просадка возрастать, и наоборот.

Все методы подразделяют на три группы: 1) водозащитные; 2) конструктивные; 3) устраняющие просадочные свойства пород.

Водозащитные мероприятия предусматривают планировку строительных площадок для отвода поверхностных вод, гидроизоляцию поверхности земли, предохранение зданий от утечек воды из водопроводов, устройство водонепроницаемых полов, покрытий, отмосток и т. д. Конструктивные мероприятия рассчитаны на приспособление объектов к возможным неравномерным осадкам, повышение жесткости стен и прочности стыков, армирование зданий поясами, применение свайных, а также уширенных фундаментов, передающих давление на фунт меньше, чем P_SL- Маломощные просадочные грунты (H_SL) прорезаются глубокими фундаментами, в том числе свайными.

Наибольшее число методов связано с устранением просадочных свойств. Их подразделяют на две группы:

• улучшение пород с применением механических методов;

• физико-химические способы улучшения.

Механические методы преобразуют породы либо с поверхности, либо в глубине толщ. Поверхностное уплотнение производят трамбовкой, замачиванием под своим весом или весом сооружения. В глубине толщ уплотнение производят с помощью грунтовых свай (песчаных, известняковых), взрывов в скважинах, замачиванием через скважины с последующим взрывом под водой и т. д. Находят применение также песчаные и грунтовые подушки, грунто-цементные опоры.

17.Грунты всех видов относят к мерзлым грунтам, если они имеют отрицательную температуру и содержат в своем составе лед.

Вечномерзлыми называют грунты, которые находятся в мерзлом состоянии непрерывно в течение многих лет (трех и более).

Мерзлые и вечномерзлые грунты в естественном состоянии при отрицательной температуре являются очень прочными и малодеформируемыми грунтами.

При замораживании и оттаивании вечно мерзлые грунты меняют свои структурные свойства. Основной особенностью таких грунтов являются их просадочность при оттаивании.

18.Структурно-неустойчивыми называют такие грунты, которые обладают способностью изменять свои структурные свойства под влиянием внешних воздействий с развитием значительных осадок, протекающих, как правило, с большой скоростью. К основным воздействиям относятся увлажнение грунтов, промерзание и оттаивание, суффозия и выветривание, внешние нагрузки, перемятие грунтов и др. Такое название они получили потому, что при определенных условиях их природная структура сравнительно резко нарушается. К структурно-неустойчивым относятся следующие грунты:

- лессовые, структура которых нарушается при замачивании их под нагрузкой;

- набухающие, которые при увлажнении способны существенно увеличиваться в объеме даже под нагрузкой;

- засоленные, песчано-глинистые отложения, в которых накопление солей произошло в процессе их формирования

сильносжимаемые грунты, деформационные и прочностные свойства которых резко изменяются при нарушении их природной структуры;

- торфы и заторфованные грунты, обладающие очень большой сжимаемостью и малой прочностью;

- мерзлые и вечномерзлые, структура которых нарушается при оттаивании.

19. Требуеться определить все компоненты нормальних Ϭ и касательных напря жений τ а также перемещений w для любой точки полупространства с коор динатами x, y,z или R и β в полярной системе. В какой то точке М , определяемой полярними координатами β

и R действует нормальное напряжение ϬR по направлению радиуса R. Согласно решения Буссинеска его величина определяется выражением:

ϬR =А(cosβ )/R2

Здесь А-коэфициент, определяемый из условия равновесия, корда сумма проекцій всех сил на вертикальную ось ровна нулю. В результате

получим что А=( 3/2)(Р/π ).

В результате получим, что

ϬR=(3/2)(Р/π R2 ).cosβ

Рассмотрим величину радиального напряжения действующего на площадке паралельной ограничивающей полупространство плоскости

и направленого по радиусу R и под углом β к линии действия Р и обозначим его как ϬRI (Рис.3.3. Ц2 ст 79).,видно что

ϬRI=ϬR cosβ

cosβ=z/R

ϬRI=(3/2)(P/π)(z2 /R4)

Раскладывая данное напряжение на три направления: Z,X иY получим, что

Ϭz =( 3/2)(P/π)(z3/R5)

τzy=(3/2)(P/π)(z3/R5) ( 3.1.)

τzx=(3/2)(P/π)(xz2/R5)

Сумма нормальних напряжений в любой точке ϴ и перемещений wz определяються выражениями:

ϴ=Ϭz + Ϭy + Ϭx= Ϭ1 +Ϭ2 + Ϭ3 =P/π(1+μ0) z/R3 ( 3.2/)

wz=P/ π CR (3.3.)

Здесь C=E0 / (1+ μ02 )- коэфициент линейнодеформируемого полупространства,E0 –модуль общей деформации, μ0 –коэфициент Пуассона,

Положение точки М на Рис.3.3.опаределяеться двумя её координатами: z и r но так как

R=( z2+r2)1/2=z(1+(r/z)2 )

То на основании одной из формул (3.1.) можно получить:

Ϭz =K(P/z2) (3.4.)

Здесь K=(3/2 π) 1/(1+ (r/z)2 )5/2

Значения К для любих точек плоупространства приводяться в справочных таблицях, например у Титовича.

Если к поверхности приложено несколько сосредоточенных сил Р1 тогда напря жения определяються по формуле:

Ϭz=K1P1/ z2+ K2P2/z2+ K3 P3 / z2 (3.5.)

Здесь коэфициент К каже определяется по таблицям в зависимости от значений отношения ri / z .

20. Этот случай соответствует напряженному состоянию под стеновыми фундаментами, подпорными стенками, насыпями и другими сооружениями, длина которых значительно превосходит их поперечные размеры:

,

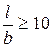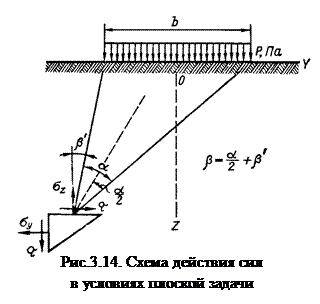где l – длина фундамента; b – ширина фундамента. При этом распределение напряжений под любой частью сооружения, выделенной двумя параллельными сечениями, перпендикулярными оси сооружения, характеризует напряженное состояние под всем сооружением и не зависит от координат, перпендикулярных к направлению загруженной плоскости.

Рассмотрим действие погонной нагрузки в виде непрерывного ряда сосредоточенных сил Р, каждая из которых приходится на единицу длины. В этом случае составляющие напряжений в любой точке М с координатами R и b могут быть найдены по аналогии с пространственной задачей:

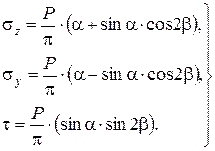(3.27)

Если соотношения геометрических характеристик рассматриваемых точек z, y, b представить в виде коэффициентов влияния K, то формулы для напряжений можно записать так:

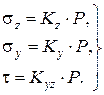(3.28)

Значения коэффициентов влияния K_z, K_y, K_yz табулированы в зависимости от относительных координат z/b, y/b (табл. II.3 приложения II).

Важное свойство плоской задачи в том, что составляющие напряжений t и s_y в рассматриваемой плоскости z0y не зависят от коэффициента поперечного расширения n₀, как в случае пространственной задачи.

dP

Задача может быть решена и для случая погонной нагрузки, любым образом распределенной по полосе шириной b. При этом элементарную нагрузку dP рассматривают как сосредоточенную силу (рис.3.15).

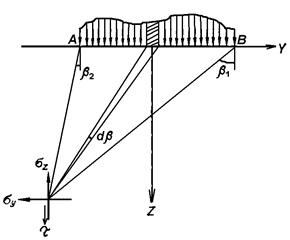
Рис.3.15. Произвольное распределение

нагрузки по ширине полосы b

Если нагрузка распространяется от точки A(b=b₂) до точки B(b=b₁), то, суммируя напряжения от ее отдельных элементов, получим выражения для напряжений в любой точке массива от действия сплошной полосообразной нагрузки.

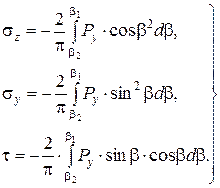(3.29)

Этот случай соответствует напряженному состоянию под стеновыми фундаментами, подпорными стенками, насыпями и другими сооружениями, длина которых значительно превосходит их поперечные размеры:

,

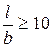где l – длина фундамента; b – ширина фундамента. При этом распределение напряжений под любой частью сооружения, выделенной двумя параллельными сечениями, перпендикулярными оси сооружения, характеризует напряженное состояние под всем сооружением и не зависит от координат, перпендикулярных к направлению загруженной плоскости.

Рассмотрим действие погонной нагрузки в виде непрерывного ряда сосредоточенных сил Р, каждая из которых приходится на единицу длины. В этом случае составляющие напряжений в любой точке М с координатами R и b могут быть найдены по аналогии с пространственной задачей:

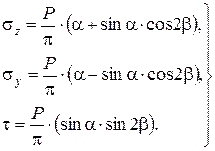(3.27)

Если соотношения геометрических характеристик рассматриваемых точек z, y, b представить в виде коэффициентов влияния K, то формулы для напряжений можно записать так:

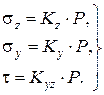(3.28)

Значения коэффициентов влияния K_z, K_y, K_yz табулированы в зависимости от относительных координат z/b, y/b (табл. II.3 приложения II).

Важное свойство плоской задачи в том, что составляющие напряжений t и s_y в рассматриваемой плоскости z0y не зависят от коэффициента поперечного расширения n₀, как в случае пространственной задачи.

dP

Задача может быть решена и для случая погонной нагрузки, любым образом распределенной по полосе шириной b. При этом элементарную нагрузку dP рассматривают как сосредоточенную силу (рис.3.15).

Рис.3.15. Произвольное распределение

нагрузки по ширине полосы b

Если нагрузка распространяется от точки A(b=b₂) до точки B(b=b₁), то, суммируя напряжения от ее отдельных элементов, получим выражения для напряжений в любой точке массива от действия сплошной полосообразной нагрузки.

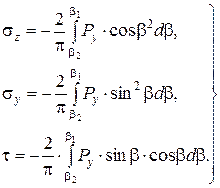(3.29)