Лабораторная работа № 1. Корреляционный анализ

Цель работы. Овладение методами исследования корреляционной зависимости между несколькими количественными случайными величинами по выборочным данным в MS Excel 2010.

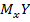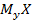Краткие сведения. Корреляционной зависимостью двух случайных величин Y и X называется функциональная зависимость условного математического ожидания (или ) одной из них от значения 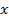(или 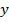) другой величины. Корреляционная зависимость может быть представлена в виде уравнения регрессии Y по X: 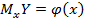или уравнения регрессии X по Y: 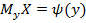. Если функция 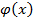линейная, то корреляционная зависимость называется линейной, если 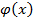нелинейная, то корреляционная зависимость называется нелинейной.

Основная задача корреляционного анализа – выявление наличия, вида и тесноты корреляционной зависимости между случайными величинами путем точечного и интервального оценивания различных (парных, множественных, частных) коэффициентов корреляции по выборке 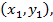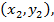… , 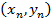из генеральной совокупности, распределенной по многомерному нормальному закону.

Для оценки наличия и тесноты корреляционной связи между двумя случайными величинами Y и X, имеющими совместное нормальное распределение, используются выборочный коэффициент корреляции и эмпирическое корреляционное отношение.

Выборочный коэффициент корреляции 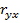используется для оценки наличия и тесноты парной линейной корреляционной зависимости

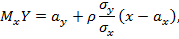
где 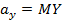, 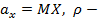генеральный (теоретический) коэффициент корреляции, и 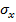- среднеквадратические отклонения величин Y и Х. Выборочный коэффициент корреляции 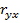является точечной оценкой генерального коэффициента корреляции 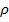и вычисляется по формуле

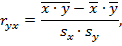
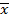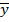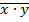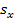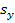где и – выборочные общие средние X и Y, – выборочное общее среднее произведения XY, и – выборочные среднеквадратические отклонения величин X и Y. Выборочный коэффициент корреляции 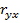показывает, на сколько величин 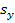изменится в среднем зависимая величина Y при увеличении аргумента X на одно 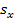и является показателем тесноты парной линейной корреляционной зависимости.

Свойства выборочного коэффициента корреляции:

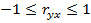· , чем больше 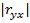, тем теснее линейная корреляционная зависимость Y и X, т.е. меньше разброс выборочных значений 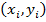относительно оцененной по выборке линии регрессии

· ;

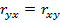· если все выборочные значения умножить на одно и то же число, то величина коэффициента корреляции не изменяется;

· при 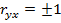корреляционная зависимость представляет линейную функциональную зависимость между Y и X, т.е. все выборочные значения 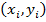лежат на оцененной линии регрессии ;

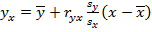· при линейная корреляционная зависимость между Y и X отсутствует их групповые средние 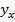и 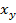совпадают с их общими средним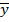и и 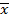, а регрессия Y по X принимает вид 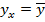. Равенство говорит лишь об отсутствии линейной корреляционной зависимости между величинами Y и X, но не об отсутствии корреляции или стохастической зависимости между Y и X.

Проверка значимости коэффициента корреляции 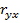осуществляется путем проверки гипотезы 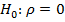, т.е. предположения об отсутствии линейной корреляционной зависимости между величинами Y и X. При справедливости этой гипотезы статистика

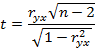
имеет распределение Стьюдента (t-распределение) с числом степеней свободы n-2, где n – объем выборки. Гипотеза 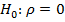отвергается при уровне значимости 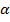(т.е. выборочный коэффициент корреляции значимо отличается от нуля), если вычисленное по выборке объема 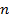значение 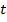удовлетворяет неравенству

,

где 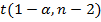– квантиль уровня 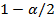распределения Стьюдента с числом степеней свободы .

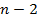Доверительный интервал надежности 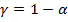для генерального коэффициента корреляции 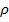при значимом выборочном коэффициенте корреляции 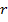строится с помощью z-преобразования Фишера

.

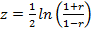Распределение статистики уже при малых объемах выборки близко к нормальному, что позволяет построить доверительный интервал для ее математического ожидания и от него перейти к доверительному интервалу для генерального коэффициента корреляции 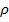, который имеет вид

,

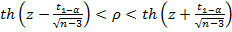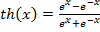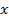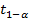где – гиперболический тангенс , а определяется по функции Лапласа из условия .

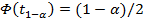Для определения наличия и тесноты любой (линейной или нелинейной) корреляционной связи используется эмпирическое корреляционное отношение Y к X

,

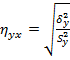которое тем больше, чем большее влияние на вариацию Y оказывает изменчивость X по сравнению с неучтенными факторами. Здесь 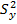– общая выборочная дисперсия величины Y, 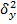– межгрупповая дисперсия Y. Свойства эмпирического корреляционного отношения:

· ;

· ;

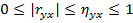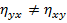· при 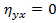корреляционная связь между Y и X отсутствует;

· при 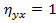между Y и X существует функциональная зависимость;

· при 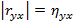между Y и X существует линейная корреляционная зависимость.

Величина 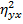называется эмпирическим коэффициентом детерминации, она показывает, какая часть общей вариации Y обусловлена вариацией X.

Многомерный корреляционный анализ исследует корреляционную зависимость совокупности случайных величин 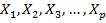имеющих совместное нормальное распределение. Корреляционная матрица 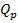, составленная из парных генеральных коэффициентов корреляции 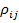величин 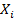и ,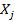

,

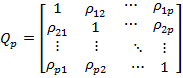характеризует линейную корреляционную зависимость между парами величин 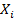и 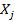этой совокупности. Основная задача многомерного корреляционного анализа состоит в оценке корреляционной матрицы 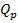по выборочным данным. Такой оценкой является матрица выборочных коэффициентов корреляции

,

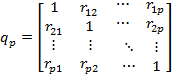в которой 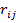– выборочные коэффициенты корреляции между величинам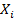и и 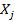. Матрицы 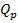и 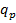симметричные, поэтому при вычислении матрицы 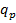приводятся только их диагональные и под диагональные элементы.

Теснота линейной корреляционной связи одной из величин 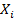с совокупностью остальных 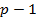величин 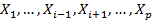оценивается выборочным коэффициентом множественной корреляции

,

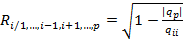где 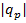– определитель матрицы 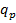, 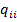– алгебраическое дополнение элемента 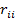матрицы 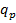. В частности, для трех величин 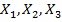выборочный коэффициент множественной корреляции 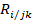вычисляется по формуле

= .

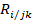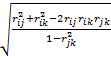Выборочный множественный коэффициент корреляции принимает значения от 0 до 1. Чем ближе значение 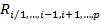к единице тем теснее линейная корреляционная связь 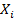с остальными величинами 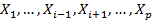. Величина 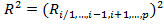называется выборочным множественным коэффициентом детерминации, которая показывает долю вариации переменной 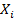объясняемую вариацией остальных переменных. Множественный коэффициент корреляции 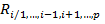значим при уровне значимости 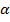, если вычисленное значение статистики

,

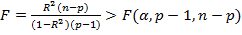где 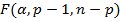значение 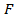- критерия на уровне значимости 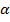при числе степеней свободы 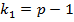и .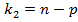

Частные коэффициенты корреляции. Если величины совокупности 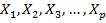коррелируют друг с другом, то на величине парных коэффициентов корреляции 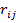переменных 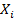и 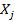сказывается влияние и других переменных совокупности, что приводит к искажению 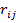. Для оценки линейной корреляционной зависимости между величинам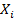и и 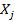, очищенной от влияния других величин совокупности, используется выборочный частный коэффициент корреляции 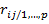.Он определяется соотношением

,

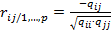где 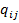, , 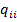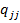алгебраические дополнения соответственно элементов 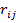, , 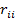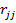матрицы выборочных коэффициентов корреляции 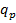. Например, для совокупности из трех случайных величин 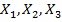выборочные частные коэффициенты корреляции 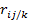находятся по формуле

.

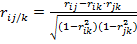Частный коэффициент корреляции принимает значения от -1 до +1. Значимость частного коэффициента корреляции при заданном уровне α определяется также как и значимость коэффициента корреляции с помощью t-статистики: если

,

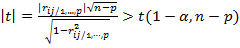то частный коэффициент корреляции 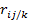значимо отличается от нуля. Матрица частных коэффициентов корреляции является также симметричной, элементы ее главной диагонали равны единице.

Содержание лабораторной работы.

1. Ввод выборочных данных для исследования корреляционной зависимости совокупности величин .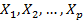

2. Построение матрицы выборочных коэффициентов корреляции и оценка наличия и тесноты линейной корреляционной зависимости между парами величин.

3. Проверка значимости наибольшего по модулю коэффициента корреляции при уровне значимости .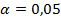

4. Построение доверительного интервала надежности 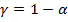для генерального коэффициента корреляции ρ между наиболее тесно связанными величинами заданной совокупности.

5. Нахождение выборочного коэффициента множественной корреляции 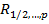и выборочного множественного коэффициента детерминации .

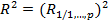6. Построение матрицы выборочных частных коэффициентов корреляции и оценка «очищенной» корреляционной зависимости 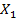с другими величинами совокупности.

7. Общее заключение о корреляционной зависимости исследуемых величин.

Выполнение работы в MS Excel.

Проведение корреляционного анализа в MS Excel-2010 приведем на примере исследования корреляционной зависимости трех величин: производительности труда ( 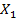) рабочих одинаковой квалификации, фондовооруженности ( 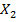) и энерговооруженности ( 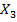) их рабочих мест. Результаты выборочного обследования приведены в таблице 1, содержащей n=14 наблюдений.

Таблица 1

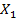	6,8	6,9	7,2	7,3	8,4	8,8	9,1	9,8	10,6	10,7	11,1	11,8	12,1	12,4
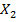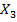	3,3	3,4	3,2	3,5	3,4	3,7	3,6	3,7	3,8		3,9	4,1	3,8	4,2

Ввод данных для исследования корреляционной зависимости рассматриваемых величин. Введем данные расположив их по столбцам А, В и С: в первых ячейках этих столбцов укажем имена переменных; значения 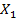разместим в ячейках А2-А15; значения 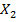в В2-В15; значения 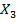в ячейках С2-С15.

Построение матрицы выборочных коэффициентов корреляции. Откроем вкладку «Данные», в группе «Анализ» выберем надстройку «Анализ данных». В открывшемся окне «Инструменты анализа» выберем функцию «Корреляция». В части «Входные данные» окна «Корреляция» в поле «Входной интервал» укажем: расположение выборочных данных на листе Excel: А1-С15; выберем группирование «по столбцам», если значения переменных расположены по столбцам, если значения переменных расположены по строкам, то выбирается «по строкам»; поставим флажок в поле «Метки в первой строке (столбце)», что указывает на то, что в первой строке (столбце) сгруппированных по столбцам (строкам) данных находятся имена переменных. В части «Параметры вывода» выбирается место расположения результатов выполнения функции «Корреляция»: «Выходной интервал» - указывается ячейка текущего листа, с которого (вправо и вниз) будет расположена корреляционная матрица 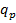; «Новый рабочий лист» - вывод корреляционной матрицы на новый рабочий лист; «Новая рабочая книга» - вывод корреляционной матрицы в новую рабочую книгу. Выберем «Выходной интервал» и ячейку Е2, с которой будет расположена корреляционная матрица. По «ОК» получим в ячейках Е2-Н5 корреляционную матрицу. Заполнение окна «Корреляция» для рассматриваемого примера приведено на рис. 1.

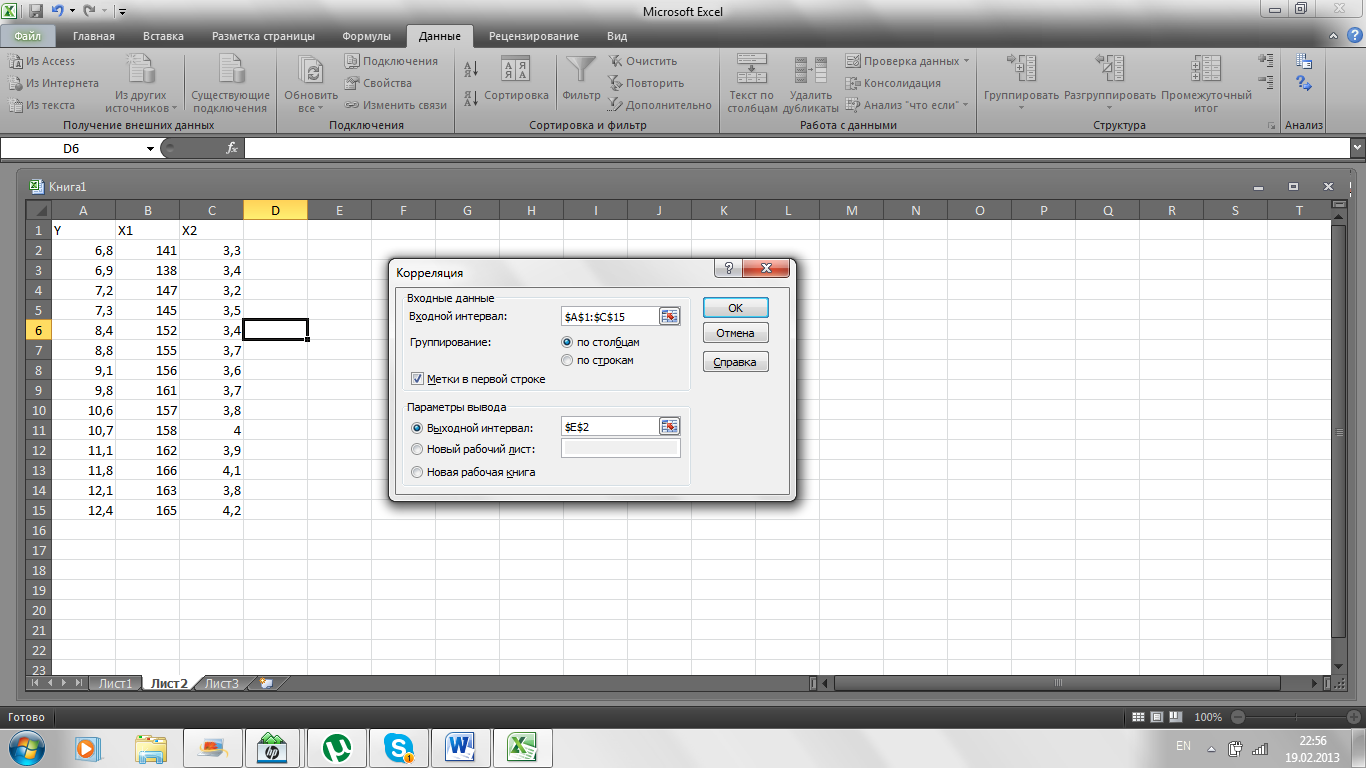
Рис. 1. Заполнение окна «Корреляция»

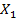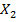Результаты выполнения функции «Корреляция» представлены на рис. 2. На рис. 2 кроме корреляционной матрицы также приведены: выборочные данные; результаты проверки значимости парных коэффициентов корреляции; доверительный интервал для генерального коэффициента корреляции между и ; выборочный коэффициент множественной корреляции 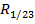; выборочный множественный коэффициент детерминации 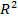; матрица частных коэффициентов корреляции. Полученные результаты снабжены краткими поясняющими записями.

Корреляционная матрица расположена в ячейках F3-H5: в ячейке F4 выборочный коэффициент корреляции 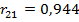, в ячейке F5 выборочный коэффициент корреляции 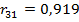, в ячейке G5 выборочный коэффициент корреляции 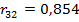. Пустые ячейки корреляционной матрицы заполним исходя из ее симметричности.

Проверка значимости коэффициентов парной корреляции. Для вычисления t-статистик, 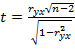, коэффициентов парной корреляции используем строку формул. Для вычисления t-статистики для 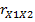выделим, например, ячейку F10, в строке формул введем

=F4*(14-2)^0,5/(1-F4^2)^0,5

По «Enter» в ячейке F10 получим значение t-статистики для 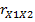. Выделив ячейку F11 и введя в строке формул =F5*(14-2)^0,5/(1-F5^2)^0,5,по «Enter» в ячейке F11 получим значение t-статистики для 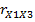. Выделив ячейку F12и введя в строке формул =G5*(14-2)^0,5/(1-G5^2)^0,5,по «Enter» в ячейке F12 получим значение t-статистики для 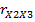(см. рис. 2). Для нахождения критической точки 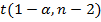распределения Стьюдента при заданном уровне значимости 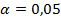выделим, например, ячейку F14. В вкладке «Формулы» выберем «Другие функции», в группе «Статистические» выберем функцию «СТЬЮДЕНТ.ОБР.2Х». В окне этой функции в поле «Вероятность» введем значение 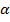, равное 0,05, в поле «Степени свободы» зададим число степеней свободы n-2, равное 12. По «ОК» в ячейке F14получим значение 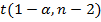, в рассматриваемом примере оно равно 2,1788. Модули t-статистик для всех коэффициентов парной корреляции превышают критическое значение 2,1788 (см. рис. 2), следовательно, все коэффициенты парной корреляции значимы.

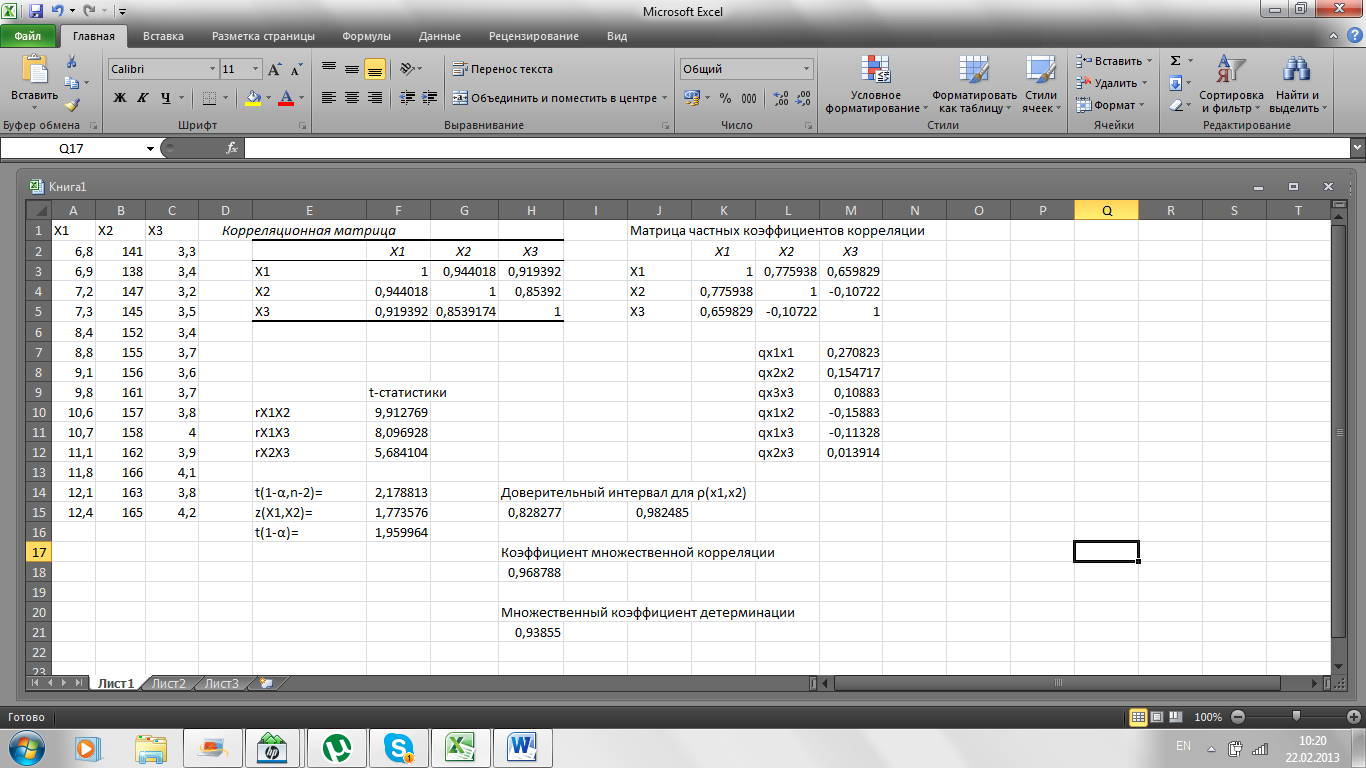
Рис.2. Результаты корреляционного анализа

Построение доверительного интервала надежности 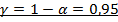для генерального коэффициента корреляции 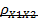. Проведем z- преобразование для выборочного коэффициента корреляции 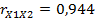. Для этого выделим, например, ячейку F15. В вкладке «Формулы» выберем «Другие функции», в группе «Статистические» выберем функцию «ФИШЕР». В окне этой функции в поле «x» введем значение коэффициента корреляции 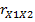. По «ОК» в ячейке F15 получим значение z, равное в этом примере 1,7736 (см. рис.2). Для вычисления значени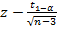й и 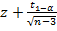предварительно найдем значение 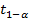. Выделим, например, ячейку F16. В вкладке «Формулы» выберем «Другие функции», в группе «Статистические» выберем функцию «НОРМ.СТ.ОБР.». В окне этой функции в поле «Вероятность» введем значение 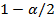, равное 0,975. По «ОК» в ячейке F16 получим значение 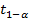, равное 1,9599 (см. рис.2).

Для получения нижней границы доверительного интервала для 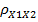выделим ячейку H15 и в строке формул введем

=ФИШЕРОБР(F15-F16/(14-3)^0,5)

По «Enter» в ячейке H15 получим искомую нижнюю границу доверительного интервала, в этом примере равную 0,8283.

Для получения верхней границы доверительного интервала для 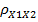выделим ячейку J15 и в строке формул введем

=ФИШЕРОБР(F15+F16/(14-3)^0,5)

По «Enter» в ячейке J15 получим искомую верхнюю границу доверительного интервала, равную в этом примере 0,9825 (см. рис.2). Аналогичным образом могут быть построены доверительные интервалы для других генеральных коэффициентов корреляции.

Нахождение выборочного коэффициента множественной корреляции 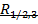и выборочного множественного коэффициента детерминации 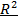. Для вычисления выборочного коэффициента множественной корреляции 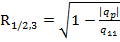выделим, например, ячейку Н18. Используя функцию вычисления определителя матрицы МОПРЕДи учитывая, что в ячейках F3-H5 находится корреляционная матрица, а в ячейках G4-H5 матрица, определитель которой равен алгебраическому дополнению 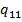элемента 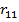корреляционной матрицы, введем в строке формул

=КОРЕНЬ(1-МОПРЕД(F3:H5)/ МОПРЕД (G4:H5))

По «Enter» в ячейке H18 получим значение выборочного коэффициента множественной корреляции 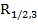, равное 0,9688.

Выделив ячейку Н21 и введя в строке формул =H18^2,по «Enter» получим в этой ячейке значение множественного коэффициента детерминации 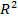, равное 0,9385.

Построение матрицы частных коэффициентов корреляции. Для этой матрицы отведем ячейки J2-M5, в ячейках J3-J5 и K2-M2 введем имена переменных X1, X2, X3, а над этими ячейками заголовок «Матрица частных коэффициентов корреляции». Для вычисления частных коэффициентов корреляции используем формулу 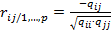. Предварительно найдем все необходимые алгебраические дополнения 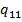, , 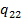, , 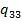, 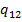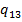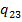разместив их в ячейках M7:M12. Напомним, что алгебраическое дополнение 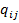элемента 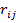матрицы 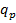находятся умножением определителя матрицы, полученной из матрицы 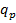вычеркиванием i-ой строки и j-го столбца, на 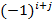. Для вычисления алгебраических дополнений используем функцию вычисления определителя МОПРЕД. Соответствующая матрица вводится в поле «Массив» окна этой функции. При вводе матрицы в поле «Массив» элементы матрицы заключаются в фигурные скобки и вводятся по строкам или столбцам, которые отделяются двоеточием, а элементы строки или столбца разделяются точкой с запятой. Например, для вычисления 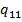выделим ячейку М7, во вкладке «Формулы» выберем группу «Математические»и в ней функцию МОПРЕД, в поле «Массив» окна этой функции введем G4:H5,по «ОК» в М7 получим значение 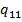. Для вычисления 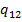, выделив ячейку М10, выберем в группе «Математические»функцию МОПРЕД. В поле «Массив» окна этой функции введем {0,944;0,8539:0,9194;1}, для учета множителя 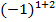в строке формул перед именем функции введем знак 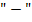, по «ОК» в М10 получим значение 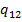. Другие алгебраические дополнения вычисляются таким же образом (см. рис. 2).

Вычисление матрицы частных коэффициентов корреляции, под нее ранее отвели ячейки K3:M5. В ячейки K3, L4, M5 введем “1”. В силу симметрии этой матрицы вычислим только ее элементы расположенные ниже главной диагонали. Выделив ячейку K4 и введя в строке формул = 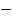M10/КОРЕНЬ(M8*M7) по «ОК» в этой ячейке получим значение 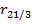.Выделив ячейку K5 и введя в строке формул = 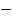M11/КОРЕНЬ(M7*M9),по «ОК» в ячейке K5 получим значение 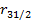.Выделив ячейку L5 и введя в строке формул = 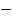M12/КОРЕНЬ(M9*M8),по «ОК» в ячейке L5 получим значение 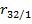. Остальные элементы матрицы частных коэффициентов корреляции (ячейки L3, M3, M4) заполняются исходя из ее симметричности (см. рис.2).

Общее заключение. Значения выборочных парных коэффициентов корреляци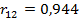и и 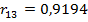говорято сильной линейной корреляционной зависимости производительности труда (Х1) от фондовооруженности (Х2) и энерговооруженности (Х3). Фондовооруженность и энерговооруженность также сильно коррелированы, 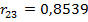. Все коэффициенты парной корреляции значимы, о чем свидетельствуют значения их t – статистик 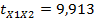, , 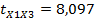, 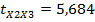модули которых превышают критическое значение t – статистики 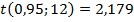. Для генерального коэффициента корреляции 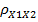95% - й доверительный интервал имеет вид (0,8283; 0,9824), что также говорит о сильной линейной корреляционной связи производительности труда и фондовооруженности. Значение множественного коэффициента корреляции Х1 с Х2 и Х3 равно 0,9688. Значение множественного коэффициента детерминации говорит о том, что 93,86% вариации производительности труда объясняется вариацией фондовооруженности и энерговооруженности. Значения частных коэффициенты корреляци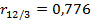и и 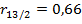говорят о том, что «чистые» влияния фондовооруженности и энерговооруженности на производительность труда существенно. Значение частного коэффициента корреляции 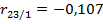говорит о незначительной отрицательной линейной корреляционной зависимости фондовооруженности и энерговооруженности.

Контрольные вопросы.

1. Сформулируйте понятия функциональной и стохастической зависимостей.

2. Какая взаимосвязь случайных величин называется корреляционной?

3. В чем заключается основная задача корреляционного анализа?

4. Для оценки какой корреляционной зависимости используется выборочный коэффициент корреляции? Каковы его свойства?

5. Как проверяется значимость коэффициента корреляции?

6. Что характеризует эмпирическое корреляционное отношение? Каковы его свойства?

7. Что характеризует эмпирический коэффициент детерминации?

8. Для совокупности трех случайных величин X, Y, Z получена матрица выборочных коэффициентов корреляции 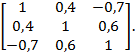Укажите наиболее тесно связанные пары величины.

9. Что оценивает выборочный коэффициент множественной корреляции?

10. Что характеризует выборочный множественный коэффициент детерминации?

11. Определите выборочный множественный коэффициент детерминации 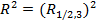по матрице выборочных коэффициентов корреляции приведенной в 8-м вопросе.

12. Определите выборочный частный коэффициент корреляции 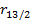по матрице выборочных коэффициентов корреляции приведенной в 8-м вопросе.

13. Проверьте значимость частного коэффициента корреляции 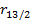, найденного в предыдущем вопросе, при объеме выборки n=19 и уровне значимости .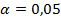