Построение математических моделей простейших экономических задач

Задача использования сырья. Для изготовления двух видов продукции А и В на предприятии используется три вида сырья. На производство единицы продукции А требуется затратить 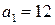кг сырья первого вида, 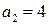кг сырья второго вида и 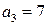кг сырья третьего вида. На производство единицы продукции В требуется затратить 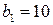кг сырья первого вида, 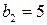кг сырья второго вида и 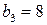кг сырья третьего вида. Производство обеспечено сырьём первого вида в количестве 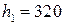кг, сырьём второго вида - 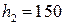кг, сырьём третьего вида - 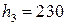кг. Нормативная стоимость единицы продукции А составляет 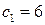грн., а продукции В- 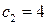грн. Составить математическую модель производства продукции А и В, для обеспечения максимальной нормативной стоимости всей продукции.

☺Пусть производится 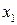единиц продукции вида А и 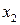единиц продукции В. Тогда нормативная стоимость всей выпускаемой продукции будет: 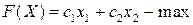. Расход каждого вида сырья этом не должен превышать его запасы, т.е. должны выполняться следующие ограничения: 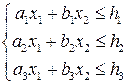Кроме того, количество произведенной продукции не может быть отрицательным. Т.е. накладывается ограничение неотрицательности переменных 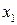и .

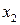Целевая функция, ограничения задачи и условие неотрицательности переменных составляют математическую модель залачи.☻

Математическая модель задачи использования сырья:

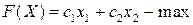
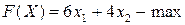
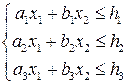
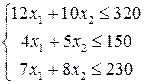
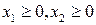
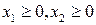
Задача о составлении рациона питания. В рационе животных используется два вида кормов: А и В. Животные должны получать три вида питательных веществ: 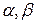и 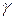. Составить рацион кормления, обеспечивающий минимальные затраты. Исходные данные приведены в таблице:

Минимально необходимое количество питательного вещества	Содержание питательного вещества в единице корма
А	В
Стоимость единицы корма

☺ Пусть животным скармливается 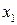кг корма вида А и 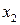кг корма вида В. Тогда целевая функция данной задачи будет иметь вид: 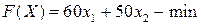. Ограничения задачи будут следующими:

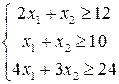. Условия неотрицательности переменных: .

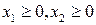Математическая модель задачи о составлении рациона:

.☻
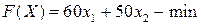
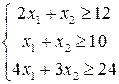
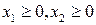