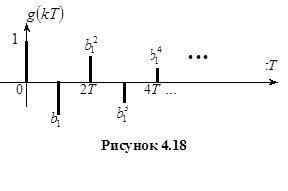Рекурсивные цифровые фильтры

Недостатком трансверсальных фильтров являются их ограниченные возможности. Рекурсия в математике означает возвращение к данным, полученным на предыдущем этапе вычислений, в радиотехнике это выливается в обратные связи.

Алгоритм рекурсивной фильтрации

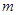– тая выборка выходного сигнала формируется как взвешенная сумма 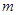– той входной выборки, некоторого количества 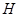предыдущих входных выборок, а также некоторого количества 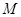предыдущих выходных выборок. Аналогично предыдущему случаю можно записать разностное уравнение рекурсивной фильтрации

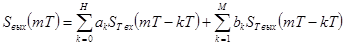,(4.53)

где 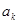– весовые коэффициенты трансверсальной части, 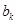– весовые коэффициенты рекурсивной части.

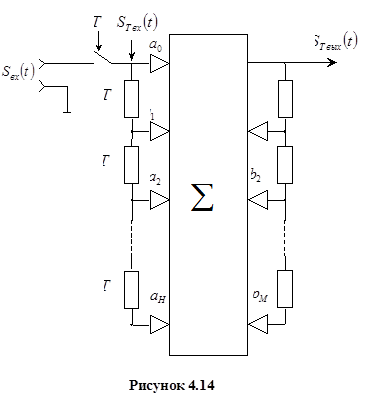
Схема алгоритма представлена на рисунке 4.14. Когда заполнятся все линии задержки фильтр будет производить суммирование 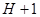входных отсчетов и 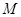выходных отсчетов.

Определим передаточную функцию, предварительно найдем изображение выходного сигнала

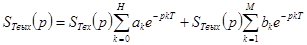, (4.54)

тогда

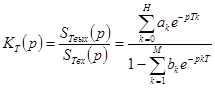. (4.55)

Оказывается, что если 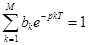, то фильтр может загенерировать.

Определим ККП и системную функцию фильтра

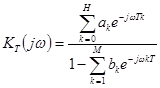, (4.56)

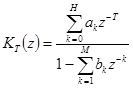. (4.57)

Импульсная характеристика будет содержать бесконечное множество импульсов. Это будет бесконечная импульсная характеристика (БИХ – фильтр).

Наличие ОС ставит проблему устойчивости, т.к. возможно самовозбуждение.

Для того, чтобы фильтр был устойчивым, полюса передаточной функции должны лежать в левой полуплоскости.

Для системной функции условие устойчивости выполняется при нахождении ее полюсов внутри круга единичного радиуса с центром в начале координат.

У устойчивого фильтра импульсная характеристика затухающая.

Рекурсивный фильтр первого порядка

Для этого фильтра 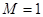и 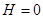. Трансверсальная часть не содержит элементов задержки.

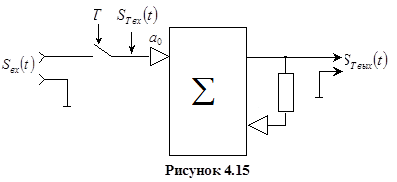
При дальнейшем анализе 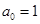. Запишем передаточную функцию

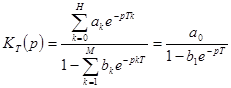, (4.58)

а ККП будет равен

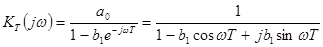. (4.59)

АЧХ в свою очередь будет равно

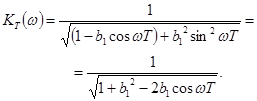(4.60)

Рассмотрим два случая

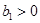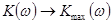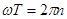1) . В этом случае при , где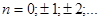

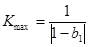. (4.61)

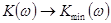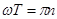при , где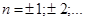

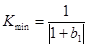. (4.62)

2) 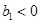. Этот фильтр выделяет частоты 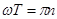, где 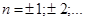, а подавляет 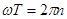, где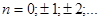

АЧХ фильтра представлены на рисунке 4.16

Если сигнал удовлетворяет теореме Котельникова, то для этого сигнала фильтр представляет собой ФНЧ (имеется ввиду случай, когда 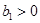, для случая 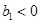это будет ФВЧ). Для сигналов с широким спектром это будет гребенчатый фильтр более качественный, чем трансверсальный.

Импульсная характеристика рекурсивного фильтра первого порядка показана на рисунке 4.17. Надо заметить, что затухающей импульсная характеристика будет при условии, что .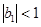

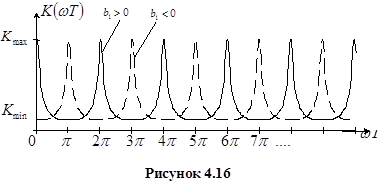
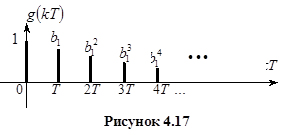
Если 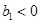, то импульсная характеристика будет знакопеременной (рисунок 4.18).