Означення дискретної випадкової величини

Випадковою називається величина, яка може набувати різних числових значень. Строгіше означення випадкової величини пов’язане з поняттям простору елементарних подій. Нехай задано простір елементарних подій W. Однозначна числова функція 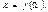яку задано на просторі елементарних подій, називається випадковою величиною. Якщо простір W дискретний, то випадкова величина дискретна. Неперервному простору елементарних подій відповідає неперервна випадкова величина.

Співвідношення між значеннями випадкової величини і їхніми ймовірностями називається законом розподілу випадкової величини.

Для дискретних випадкових величин закони розподілу можуть задаватися множиною значень, що їх набуває випадкова величина, і ймовірностями цих значень.

Якщ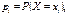о то 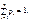або, якщо величина набуває зліченної множини значень, то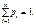

Закони розподілу дискретних випадкових величин задаються у табличній формі (подаються значення випадкової величини і їхні ймовірності), аналітичній (наводиться формула, за якою обчислюються ймовірності для заданих значень випадкової величини), графічній (у прямокутній системі координат задається набір точок 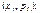сполучивши точки відрізками прямих, дістане­мо многокутник розподілу ймовірностей). Універсальним способом задання закону розподілу ймовірностей є функція розподілу 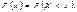Для дискретних величин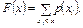

Функція розподілу — неспадна, неперервна зліва,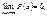

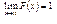
Біноміальний закон розподілу

Імовірності в цьому законі визначаються за формулою 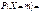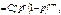m = 0,1,2, …, n. Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з імовірністю р. Частота настання події А має біноміальний закон розподілу. Імовірнісна твірна: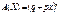

Закон розподілу Пуассона

Дискретна випадкова величина має розподіл Пуассона, якщо вона набуває зліченної множини значень 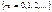з імовірностями 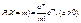Цей розподіл описує кількість подій, які настають в однакові проміжки часу за умови, що ці події відбуваються незалежно одна від одної зі сталою інтенсивністю. Розподіл Пуассона розглядається як статистична модель для кількості альфа-частинок, що їх випромінює радіоактивне джерело за певний проміжок часу; кількості викликів, які надходять на телефонну станцію за певний період доби; кількості вимог щодо виплати страхових сум за рік; кількості дефектів на однакових пробах речовини і т. ін. Розподіл застосовується в задачах статистичного контролю якості, у теорії надійності, теорії масового обслуговування. Математичне сподівання і дисперсія в цьому розподілі однакові і дорівнюють а. Для цього розподілу складено таблиці щодо різних значень 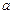(0,1 – 20). У таблицях для відповідних значень а наведено ймовірності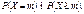

Якщо у схемі незалежних повторних випробувань n велике і р або 1 – р прямують до нуля, то біноміальний розподіл апроксимується розподілом Пуассона, коли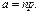

Ймовірна твірна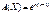

25. Числові характеристики розподілу Біноміального закону розподілу:

Імовірності в цьому законі визначаються за формулою 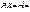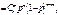m = 0,1,2, …, n. Закон справджується для схеми незалежних повторних випробувань, у кожному з яких подія А настає з імовірністю р. Частота настання події А має біноміальний закон розподілу. Числові характеристики розподілу:

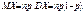
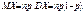Пуасонівський закон: M(X)=a=np; D(X)=a; P(X)=a.