Исследование распределения напряжения в длинных линиях.

Лабораторная работа №23

При подготовке к выполнению лабораторной работы необходимо: 1) прочитать по учебнику [1] § 10.2; 2) изучить описание данной работы; 3) заготовить табл. 23.1; 4) выполнить предварительный расчёт; 5) ответить на вопросы для самопроверки.

Цель работы: экспериментально исследовать распределение напряжений вдоль однородной длиной линии при различных значениях сопротивлений нагрузки.

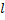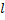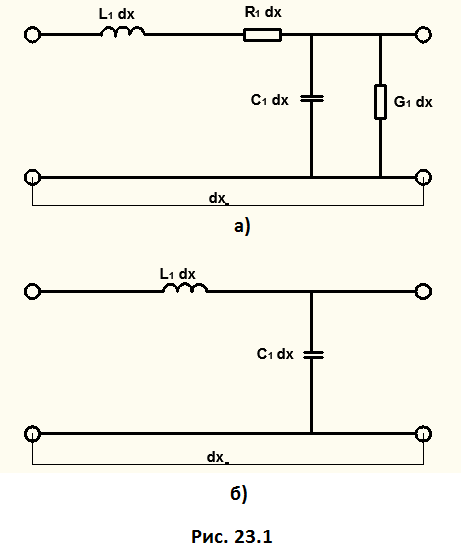
Линии передачи энергии, геометрическая длина которых много меньше длины волны λ, могут быть представлены схемами замещения с сосредоточенными параметрами, а линии, геометрическая длина которых соизмерима с длиной волны λ, - эквивалентными схемами с распределёнными параметрами. Такие линии называют длинными. На практике длинными считают линии, у которых 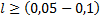λ. В общем случае каждый элементарный отрезок линии имеет индуктивность L1, емкость С1, сопротивление потерь R1 и проводимость потерь G1 (рис. 23. 1, а). Параметры L1, С1, R1, G1 называют погонными. Если выполняются условия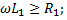 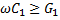( что имеет место на высоких частотах ), то такую линию считают линией без потерь (рис 23.1, б).

Обычно в реальной двух проводниковой или кабельной линии индуктивность и ёмкость равномерно распределяются вдоль линии. Электромагнитная волна распространяется вдоль линии с конечной скоростью 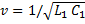. Следовательно, отклики в различных точках длинной линии появляются не в момент подключения генератора к цепи, а несколько позже, причём время запаздывания 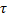зависит от длины линии и скорости распространения волны: 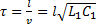. Линия без потерь является идеальной линией задержки. На практике геометрическая длина линий, необходимая для получения времени задержки всего в единице микросекунд, оказывается чрезвычайно большой. Например, у кабелей распространённых типов длиной 200 м время задержки составляет порядка единиц микросекунд. Поэтому в реальных устройствах используют искусственные длинные линии, представляющие собой большое число каскадно включённых звеньев с сосредоточенными параметрами. Чем больше звеньев имеет искусственная линия тем более схожи процессы, происходящие в ней, с процессами, получающимися в цепи с распределенными параметрами. Определим, какую частоту должен иметь генератор подключенный к искусственной линии, состоящей из п звеньев, чтобы эквивалентная длина такой линии была равна длине волны генератора. Время задержки искусственной линии: 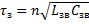, где 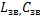– индуктивность и ёмкость каждого звена искусственной линии. Таким образом, искусственная линия, состоящая из n звеньев, эквивалентна двух проводной линии с погонными индуктивностью 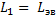и ёмкостью 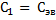такой длины, при которой получается такое же время задержки , как у искусственной линии. Частота и период колебаний связаны соотношением 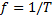. Если время задержки линии равно периоду колебаний Т, то расстояние, проходимое сигналом за это время, равно длине волны λ. Следовательно 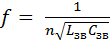. В свободном пространств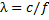е , где 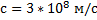– скорость света. При

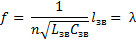
Откуда 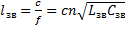. Таким образом, искусственная линия, состоящая из n звеньев, имеющая индуктивность 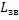и ёмкость 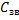в каждом звене, на частоте 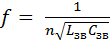эквивалентна линии длиной 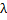, а на частоте, в четыре раза меньшей, - линии длиной .

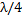Каждая линия характеризуется волновым сопротивлением Zв и постоянной распространения .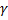

В общем случае волновое сопротивление линии 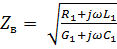. В линиях без потерь волновое сопротивление имеет чисто резистивный характер; 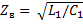. Коэффициент распространения 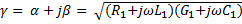.В линии без потерь 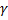имеет чисто резистивный характер: 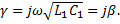Вещественная часть постоянной распространения характеризует затухание колебаний в линии, а мнимая – изменение фазы колебаний вдоль линии. Во всех случаях, когда линия нагружена на резистор, сопротивление которого отличается от волнового, в линии имеет место отражённая волна, причём коэффициент отражения от нагрузки 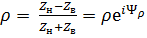, где 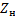– сопротивление нагрузки.

В зависимости от значений сопротивления нагрузки, на которое нагружена линия, могут иметь место следующие режимы работы линии: а) режим холостого хода ( линия разомкнута на конце; 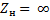); б) режим короткого замыкания ( линия замкнута на конце; 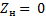); в) режим работы на согласованную нагрузку (линия нагружена на резистор, сопротивление которого равно волновому 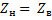); г) режим работы на не согласованную нагрузку ( линия нагружена на резистор, сопротивление которого не равно волновому; 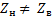); д) режим работы при замыкании линии на элементы с чисто реактивным сопротивлением ( ).

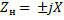В общем случае комплексные действующие значения напряжения и токов в любой точке линии определяется из выражений

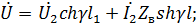(23.1)

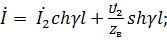(23.2)

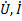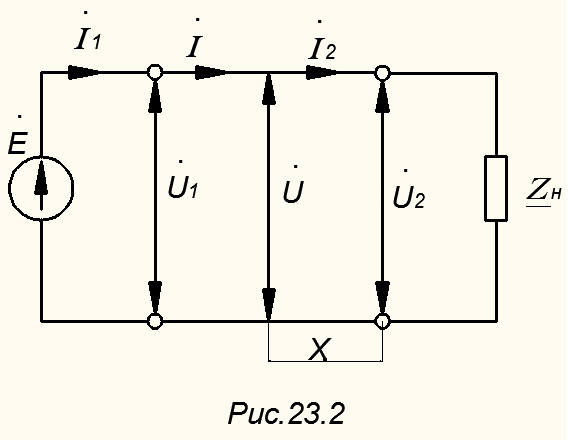
Где – комплексные действующие значения напряжения и тока на расстоянии 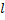от конца линии ( рис. 23.2); 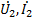– комплексные действующие значения напряжения и токов в конце линии, т.е. на нагрузке. Для линии без потерь выражения (23.1) и (23.2) принимают вид

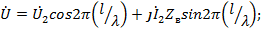(23.3)

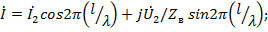(23.4)

При работе в режиме холостого хода ( )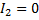

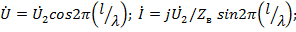
Модули напряжения и тока ; .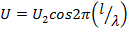

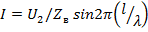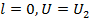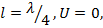
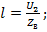При ; при при 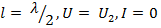и т.д.

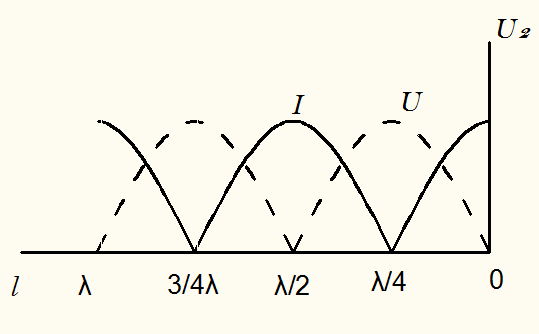
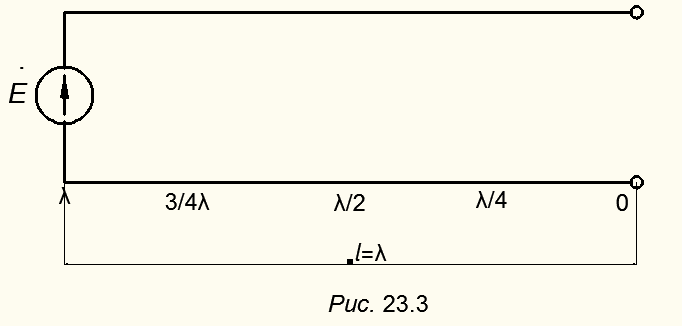
Распределение напряжений и токов в разомкнутой линии длиной 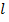показаны на рис. 23.3. Обратим внимание на то, что на рисунке дано распределение действующих ( амплитудных) значений токов и напряжений, а не мгновенных. При холостом ходе 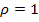, т.е. амплитуды падающей и отражённой волн равны между собой. В точках, где падающая и отражённая волны совпадают по фазе, получаются пучности, а в точках, где они противоположны по фазе, - узлы. Волны, образующие распределение напряжений и токов с узлами и пучностями, называют стоячими. В режиме стоячих волн амплитудное значение напряжения в каждой токе лини различно и зависит т расстояния до конца линии. Режим стоячих волн имеет место также при коротком замыкании на выходе линии ( ):

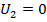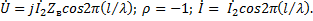
Распределения токов и напряжений в короткозамкнутой линии показаны на рис. 23.4.

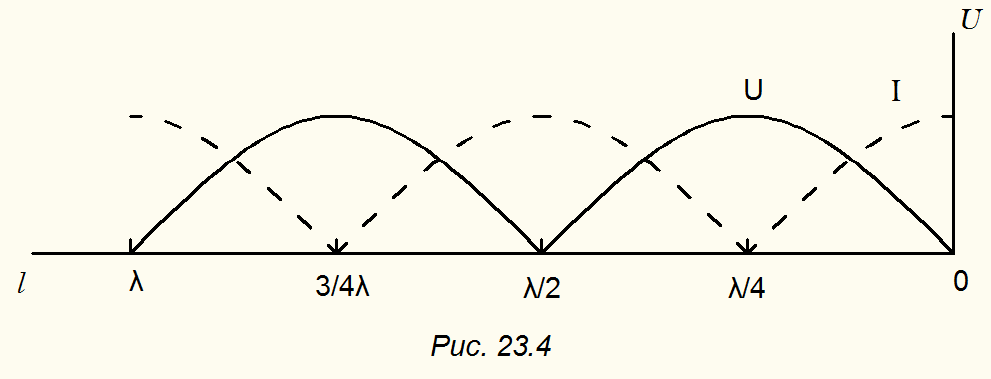
Если линия замкнута на резистор сопротивлением, равным волновому, то коэффициент отражения 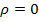; в линии имеют место только падающие волны. Такой режим называют режимом бегущих волн. Так как 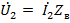, то выражения (23.3) и (23.4) принимают вид

.

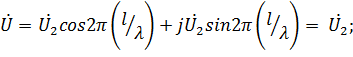
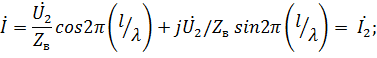
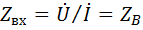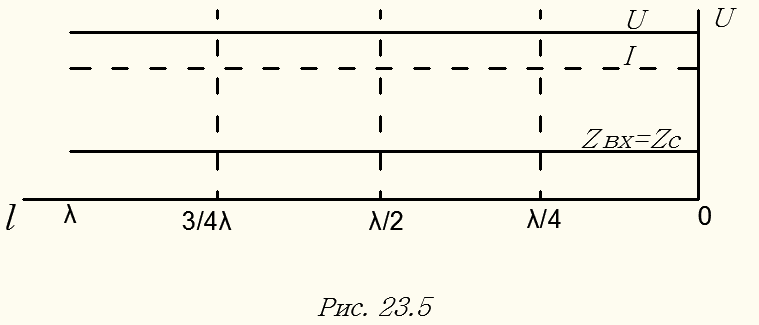
Таким образом, при согласованной нагрузке амплитуда напряжения в любой точке линии без потерь равна амплитуде напряжения на входе линии, ток 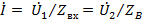, а входное сопротивление в любом сечении равно волновому сопротивлению линии (рис. 23.5).

При не согласованной нагрузке 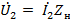. В этом случае выражения (23.3) и (23.4) принимают вид

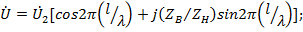
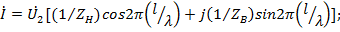
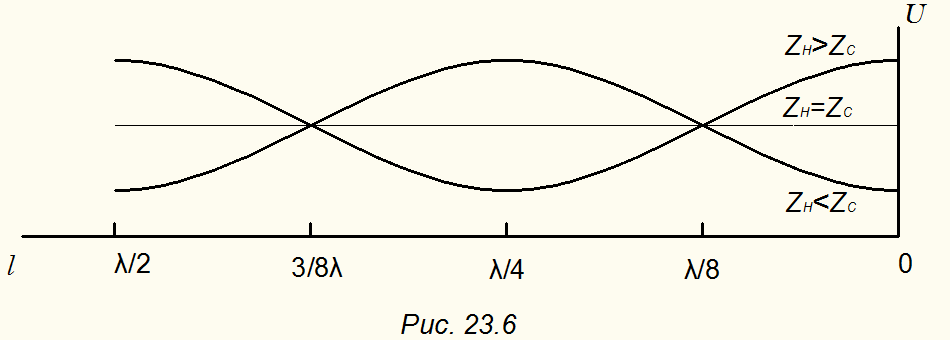
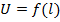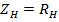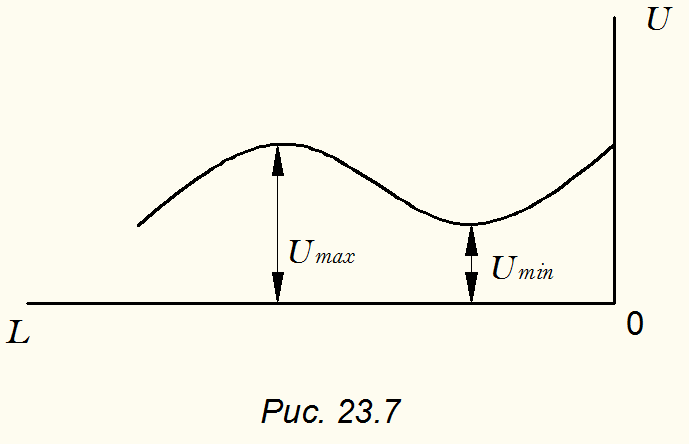
При этом имеет место режим смешанных волн, который можно рассматривать как наложение режимов бегущих и стоячих волн. Кривые для различных значений показаны на рис. 23.6. Чем больше различие между 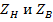тем больше значения между минимальными и максимальными напряжениями ( рис. 23.7). Если известны 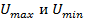, например, из эксперимента, то коэффициент отражения 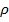и коэффициент бегущей волны 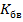можно определить из выражений

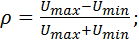
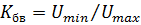
Коэффициентом стоячей волны называют величину, обратную коэффициенту бегущей волны: .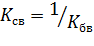

При нагрузке линии на элементы с чисто реактивным сопротивлением в линии образуются стоячие волны так же, как и в режиме холостого хода и короткого замыкания. Однако при этом на выходе линии нет ни узла, ни пучности напряжения, поскольку они сдвигаются вдоль линии. При индуктивной нагрузке узлы и пучности напряжения смещаются влево ( в сторону генератора), при ёмкостной нагрузке – вправо ( в сторону нагрузки).

Линию, замкнутую на элемент с чисто реактивным сопротивлением, можно заменить эквивалентным отрезком линии, у которой входное сопротивление равно сопротивлению реактивного элемента. Например, ёмкостной элемент можно заменить разомкнутым отрезком линии длиной менее 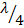, а индуктивный – короткозамкнутым отрезком линии длиной менее 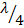и т.д. Производя такую замену, можно определить распределение напряжений и токов в эквивалентной линии с учётом добавочного отрезка. При добавлении разомкнутого отрезка линии на её конце будет пучность напряжения, а при добавлении короткозамкнутого – узел напряжения. Для сдвига узлов и пучностей напряжения вправо на 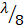необходимо подключить конденсатор, ёмкость которого находят из уравнения 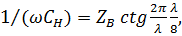откуда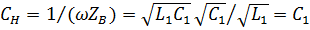

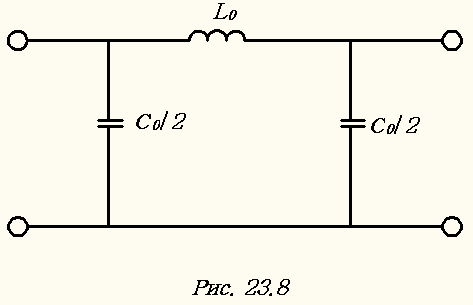
Для выполнения экспериментов используют искусственную линию, состоящую из 16 одинаковых звеньев. От точек соединения звеньев имеются отводы, все звенья пронумерованы, причём нумерацию производят с конца линии. Данную линию можно рассматривать как каскадное соединение П-образных звеньев (рис.23.8). Сопротивление потерь каждого звена линии не превышает 1-2 Ом. В качестве реактивной нагрузки использовать .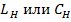

Предварительный расчёт

1. При 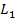= 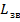, 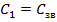рассчитать длину линии 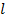, которой эквивалентна искусственная линия; частоту 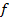, при которой на линии укладывается одна длина волны 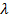. Результаты занести в табл. 23.1.

2. Сравнить сопротивление потерь звена 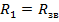со значением 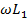. Если 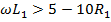, то такую линию можно считать линией без потерь. Проводимость потерь 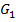считать пренебрежимо малой.

3. Определить волновое сопротивление 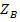и постоянную 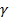данной линии.

4. Рассчитать и построить кривые распределения действующих значений напряжения вдоль линии для режимов холостого хода и короткого замыкания, если напряжение пучности равно 2,7 В ( ).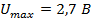

Примечание. Следует иметь в виду, что достаточно произвести расчёт для одной четверти длины волны, так как при дальнейшем увеличении длины линии распределения напряжений и токов повторяются.

5. Построить кривые 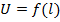при индуктивной и ёмкостной нагрузке, если 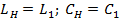(табл. 23.1).

Задание. Исследовать распределение напряжений вдоль линии при различных нагрузках.

Порядок выполнения работы

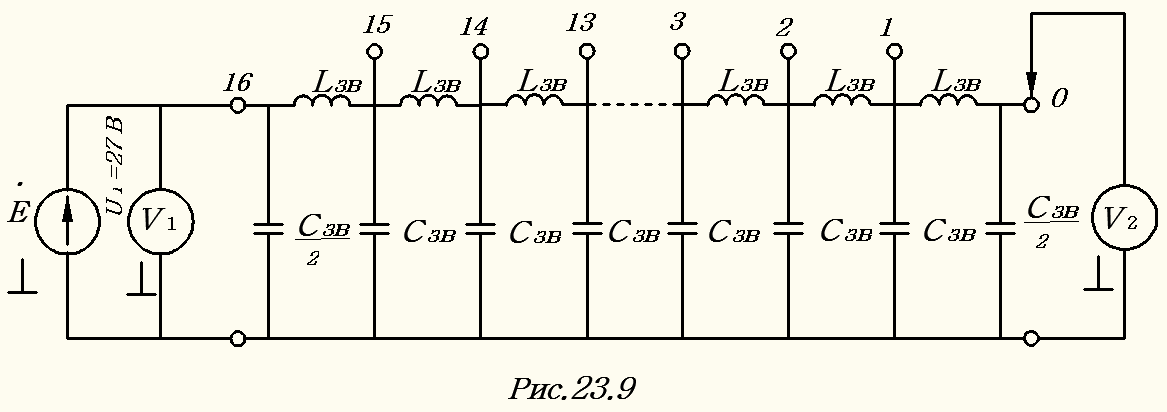
1. Собрать цепь по схеме рис.23.9. На генераторе установить частоту 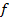, равную получившейся в п.1 предварительного расчёта, а на входе линии – напряжение 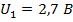. Корпусный вывод вольтметра 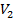подключить к общей точке линии, а потенциальный – к точке 4 линии, т.е. к точке, в которой имеется узел напряжения, поскольку эта точка отстоит на четверть длины волны от конца линии ( на конце разомкнутой линии получают пучность напряжения). Медленно вращая лимб “Частота генератора” в обе стороны, найти в районе частоты 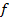положение, при котором вольтметр 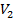покажет минимальное напряжение. Найденная частота и является той частотой, при которой на линии укладывается одна волна.

2. Подключить потенциальный вывод вольтметра 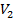поочерёдно ко всем отводам линии и снять зависимость 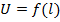. Результаты измерений занести в табл. 23.1.

3. Уменьшить напряжение 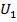до нуля (чистота генератора остаётся без изменений), закоротить линию на конце. Вольтметр 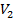подключить к точке 4 линии ( в короткозамкнутой линии в этой точке будет пучность напряжения, поскольку на конце получается узел). Установить на входе линии такое напряжение, при котором вольтметр 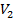показывает 2,7 В. Измерить напряжение на каждой точке линии.

4. Нагрузить линии на резистор, сопротивление которого равно волновому. Установить на магазине сопротивлений сопротивление 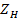, а на входе - линии напряжение 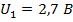. Снять характеристику .

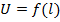5. Подключить к линии нагрузку 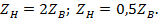Снять характеристик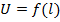и при 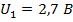= const.

6. Подключить к линии конденсатор 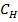. Снять характеристику .

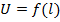7. Подключить к линии катушку 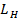. Снять характеристику .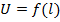