Математический , пружинный и физический маятник

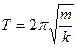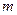Период колебаний тела, подвешенного на пружине (пружинный маятник) , где - масса тела; 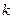- жесткость пружины

Период колебаний математического маятника 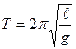, где 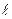- длина маятника, 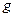- ускорение свободного падения.

Период колебаний физического маятника 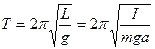, где 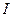- момент инерции колеблющегося тела относительно оси колебаний; 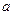- расстояние центра масс от оси колебаний: 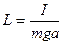- приведенная длина физического маятника

ЗАДАНИЯ И УПРАЖНЕНИЯ

1. Как между собой связаны амплитуды скорости и амплитуда колебаний при гармонических колебаниях?

2. По какой траектории будет двигаться шарик математического маятника, если нить маятника пережечь в тот момент, когда шарик проходит положение равновесия?

3. Как зависит период колебаний математического маятника от географической широты места?

4. Чему равен период колебаний потенциальной энергии, если известна частота колебаний груза?

5. Как изменится период вертикальных колебаний груза, висящего на двух одинаковых пружинах, если от последовательного соединения пружин перейти к параллельному их соединению?

6. Если частица совершает гармонические колебания с амплитудой А, то какой путь она проходит за один период?

ЗАДАЧИ

1. Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой А=8 см. Определите жесткость пружины, если известно, что максимальная кинетическая энергия груза составляет 0,8 Дж.

2. Если увеличить массу груза, подвешенного к спиральной пружине, на 600 г, то период колебаний груза возрастет в 2 раза. Определите массу первоначально подвешенного груза.

3. Пружинный маятник совершает гармонические колебания. Через сколько времени он первый раз отклонится от положения равновесия на расстояние, равное одной третьей амплитуды колебаний, если период колебаний 2 с, начальная фаза .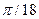

4. К спиральной пружине подвесили грузик, в результате чего пружина растянулась на 9 см. Каков будет период колебаний грузика, если его немного оттянуть вниз и отпустить?

5. Гиря, подвешенная к пружине, колеблется по вертикали с амплитудой 4 см. Определить полную энергию колебаний гири, если жесткость пружины равна .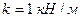

6. Найти отношение длин двух математических маятников, если отношение их периодов равно 1,5.

7. Математический маятник длиной 1 м установлен в лифте. Лифт поднимается с ускорением 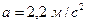. Определить период колебаний маятника.

8. Два математических маятника имеют одинаковую массу, длину, отличающуюся в 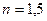раза, и колеблются с одинаковой угловой амплитудой. Определите, какой маятник обладает большей энергией и во сколько раз.

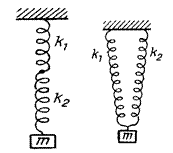
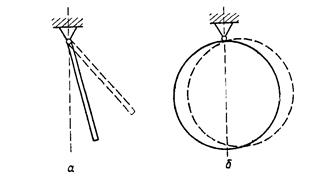
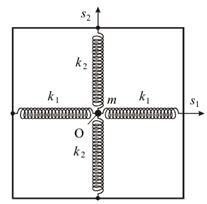
9. Груз массы 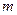подвешен к двум пружинам, соединенным «последовательно» (рис.а) и параллельно (рис.б). Определить частоты колебаний груза, если жесткость пружин задана.

10. Период колебаний математического маятника длиной 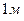равен 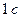. Каким станет период этого маятника при длине 0,5 м?

11. Маятник длиной 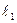совершает колебания с частотой 15 Гц. При длине 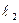он совершает колебания с частотой 10 Гц. Найти отношение .

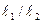12. Маятник длиной 0,25 м совершает 120 колебаний в течение 120 с. Чему равно ускорение свободного падения?

13. Вычислить длину маятника, который установлен на экваторе, если его период равен 2 с. Ускорение свободного падения на экваторе .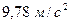

14. Как изменится период колебаний маятника, если его перенести с Земли на Луну? Ускорение свободного падения на Луне .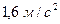

Физический маятник

15. Диск радиусом 24 см колеблется около горизонтальной оси, проходящей через середину одного из радиусов, перпендикулярно плоскости диска. Определить приведенную длину и период колебаний.

16. Физический маятник представляет собой стержень длиной 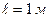и массой 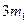с прикрепленным к одному из его концов обручем диаметром 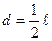и массой 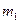. Горизонтальная ось маятника О проходит через середину стержня перпендикулярно ему. Определить период колебаний.

17. На стержне длиной 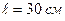укреплены два одинаковых грузика: один в середине стержня, другой- на одном из его концов. Стержень с грузиками колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определите приведенную длину и период колебаний.

18. Тонкий обруч, повешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус обруча 30 см. Вычислить период колебаний обруча.

19. Однородный диск радиусом 30 см колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Каков период колебаний?

20. Из тонкого однородного диска радиусом 20 см вырезали часть, имеющую вид круга радиусом 10 см. Оставшаяся часть диска колеблется около горизонтальной оси, походящей через точку О и совпадающей с одной из образующих цилиндрической поверхности диска. Найти период колебаний такого маятника.

21. Математический маятник длиной 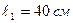и физический маятник в виде тонкого прямого стержня длиной 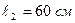синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние центра масс стержня от оси колебаний.

22. Физический маятник представляет собой тонкий однородный стержень длиной 35 см. Определите, на каком расстоянии от центра масс должна быть точка подвеса, чтобы частота колебаний была максимальна.

23. Однородный диск радиусом 20 см колеблется около горизонтальной оси, проходящей на расстоянии 15 см от центра диска. Определите период колебаний диска относительно этой оси.

24. Найти частоты малых колебаний следующих физических маятников: 1) однородного стержня длиной 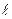и массой 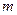; 2) однородного диска массы 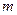и радиуса .

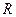Семинар 14

Сложение колебаний

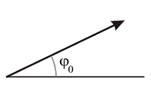Метод векторных диаграмм (сложение колебаний одного направления).

Гармонические колебания допускают наглядную графическую интерпретацию. Ее смысл состоит в том, что каждому гармоническому колебанию с частотой 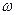можно поставить в соответствие вращающийся с угловой скоростью 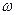вектор, длина которого равна амплитуде 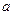, а его начальное положение задается углом 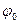, совпадающим с начальной фазой.

Мгновенное положение вектора определяется углом .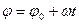

С помощью векторных диаграмм легко сложить гармонические колебания с одинаковыми частотами, направленные вдоль одной прямой

.

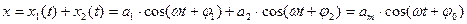Амплитуду 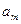и начальную фазу 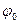суммарного колебания с той же частотой 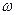можно рассчитать по формулам: