Расчет статически определимых стержневых систем

Статически определимая стержневая система – это система, в которой все неизвестные реакции опор и внутренние усилия можно определить из уравнений равновесия (статики).

Для «решения» любой стержневой системы необходимо выделить в ней объект равновесия. В связи с этим, все системы можно разделить на два типа:

1 тип – системы, состоящие из абсолютно жестких (недеформируемых) стержней и одиночных невесомых (деформируемых) стержней. Для стержневых систем этого типа объектами равновесия являются недеформируемые стержни.

2 тип – системы, состоящие из нескольких деформируемых стержней, соединенных в одной точке. Точки соединения двух и более стержней называются узлами, которые и являются объектами равновесия для систем 2-го типа.

Все соединения в элементах систем шарнирные, однако существуют определенные правила, по которым вводятся реакции и усилия в стержнях:

- в шарнире, соединяющем абсолютно жесткий элемент системы с «землей» или с другой конструкцией, всегда возникают две реакции – горизонтальная 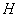и вертикальная ;

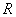- в шарнире, соединяющем деформируемый стержень с абсолютно жестким стержнем или с другой конструкцией, всегда возникает одна реакция, направленная вдоль этого стержня и равная по величине усилию, возникающему в нем.

В абсолютно жестких стержнях никогда не возникает внутренних усилий, они не деформируются!

- в шарнире, соединяющем несколько деформируемых стержней (узловой шарнире), возникают усилия, направленные вдоль этих стержней и сходящиеся в этом узле.

Порядок решения большинства задач о проверке прочности статически определимых стержневых систем при расчете по допускаемым напряжениям сводится к следующим этапам:

1) находим внутренние усилия (продольную силу при растяжении-сжатии) и выявляем опасные сечения;

2) определяем напряжения;

3) после выявления максимальных напряжений используем условие прочности (формулы (2.26), (2.28), (2.32)) при растяжении-сжатии).

Пример 11.

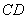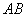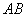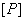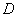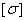Абсолютно жесткий брус поддерживается стальным стержнем , имеющим площадь поперечного сечения 100 мм² (рис.2.25, а). Определить из условия прочности стержня допускаемую нагрузку и проверить, обеспечена ли жесткость системы, если допускается перемещение сечения бруса под действием силы не более 2 мм. Допускаемое напряжение принять равным =150 МПа, модуль упругости 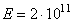Па.

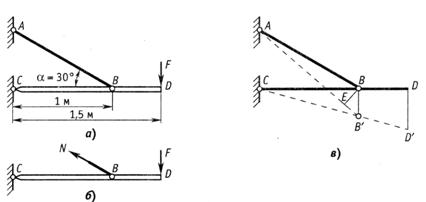
Рис.2.25

Решение.

Используя метод сечений, определим соотношение между продольной силой 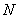в стержне 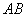и нагрузкой . Из условия равновесия сил (рис.2.25, б) находим

; ; .

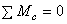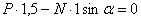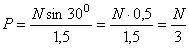Допускаемая продольная сила 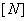для стержня 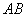из условия его прочности

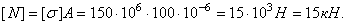
Допускаемая нагрузка на систему

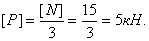
При нагружении системы стержень 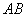удлиняется на 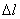, а абсолютно жесткий брус поворачивается, оставаясь прямолинейным. Система после деформации стержня 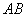показана штриховой линией на рисунке 2.25, в. Из треугольника 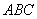определяем длину 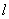стержня 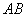: 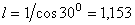м.

На основании принципа начальных размеров принимаем, что значение угла 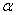не изменяется, а точк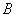и и 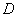перемещаются по вертикали.

Из прямоугольного треугольника 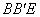находим

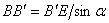; так как 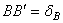, , 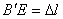то

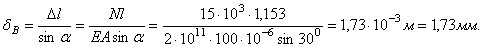
Перемещение точки 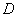определяем из подобия треугольников 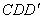и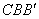

;

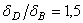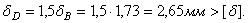
Жесткость системы не обеспечена.

Следует заметить, что нельзя повысить жесткость системы, применив для стержня 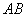более прочную сталь, так как характеристикой свойств материала, влияющей на жесткость, является модуль упругости, значение которого для всех марок сталей примерно одинаково. Повысить жесткость системы можно, либо увеличив площадь поперечного сечения стержня 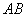, либо уменьшив его длину.

Пример 12.

Определить допускаемую нагрузку 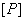для системы из двух стержней, изготовленных из дюралюминиевых труб одинакового поперечного сечения (рис.2.26, а). Допускаемое напряжение принять 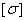= 100 МПа.

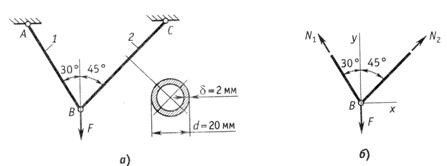
Рис.2.26

Решение.

Используя метод сечений, вырезаем узел 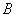и из уравнений равновесия сил

; ;

;

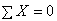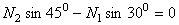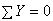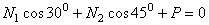
находим неизвестные продольные силы, возникающие в стержнях, через нагрузку (рис.2.26, б)

; .

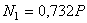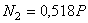Допускаемую нагрузку 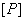определяем из условия прочности наиболее нагруженного стержня 1:

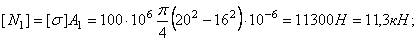
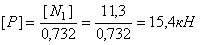
Следует отметить, что стержень 2 недогружен. Напряжение в нем

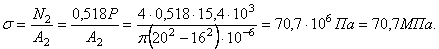
что примерно на 30% ниже допускаемого. Для стержня 2 можно использовать трубу меньшего поперечного стержня.

Пример 13.

Рассмотрим стержневую систему, состоящую из абсолютно жесткого (недеформируемого) стержня 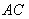, шарнирно закрепленного в точке и невесомого (деформируемого) стержня , шарнирно закрепленного по концам, загруженную в точке сосредоточенной силой (рис. 2.27).

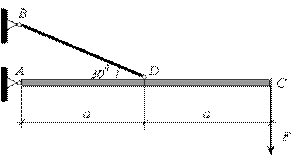
Рис.2.27

Решение.

Объектом равновесия в данном случае будет являться стержень 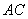, для которого и будем составлять уравнения равновесия.

Под действием внешней нагрузки, на основании введенных выше правил, в точке 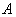будут возникать две реакци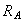и и 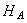, а в стержне 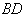возникает усилие 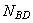, направленное по стержню (рис. 2.28).

Определим несущую способность (грузоподъемность) заданной системы, то есть допустимую нагрузку , если площадь сечения стержня 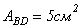, расчетное сопротивление материала стержня .

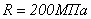Для этого можно составить следующие уравнения равновесия:

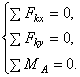
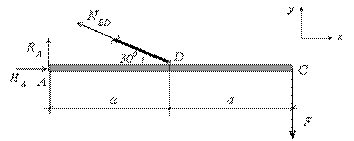
Рис.2.28

Поскольку в конечном итоге решение задачи будет сводиться к определению усилия в стержне 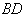, то оставляем в рассмотрении уравнение равновесия, содержащее только 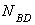, то есть уравнение моментов относительно точки 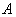. Распишем данное уравнение:

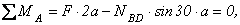
отсюда неизвестное усилие

.

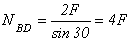Записываем условие прочности для стержня 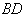и выражаем нагрузку :

,

.
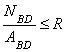
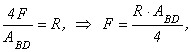
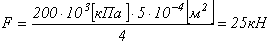