Степенная и показательная функция

77) Свойства степени с натуральным показателем. Степенная функция с натуральным показателем. Её свойства и график.

Свойства степени:

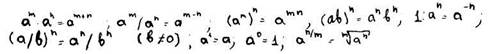
График и свойства степенной функции.

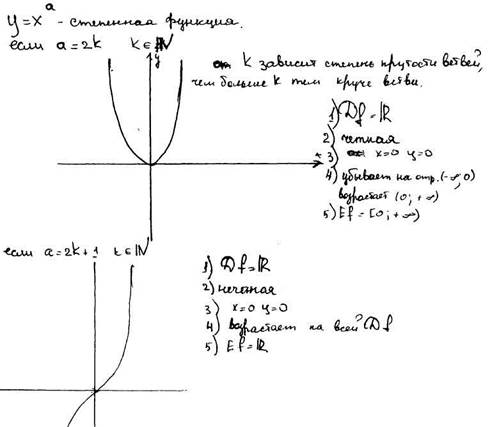
78) Доказать свойства степени с целым показателем. Степенная функция с целым показателем, её свойства и график.

Арифметический и алгебраический корень. Показать на примере существование арифметического корня.

Корнем n-степени из числа а называется такое число n-степень которого равна а.

Арифметическим корнем из числа а называется неотрицательный корень из этого числа.

Примером арифметического корня служит график корня.

80) Степенная функция корень n-степени из х. Доказать её свойства и построить график.

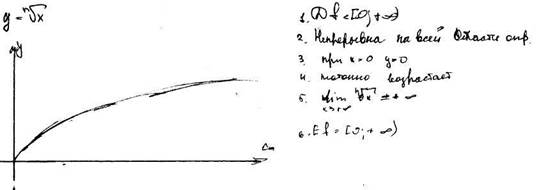
Свойства степени с рациональным показателем. Степенная функция с рациональным показателем, доказать свойства и построить график.

Показательная функция, доказать свойства и построить график.

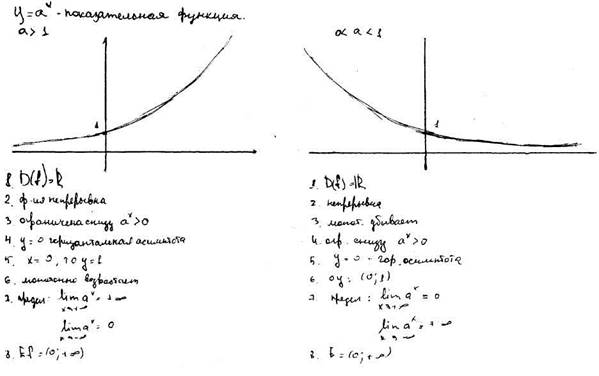
Логарифм числа и логарифмическа функция.

Логарифм числа. Основное логарифмическое тождество. Доказать теорему о логарифме произведения, частного, степени.

Показатель степени, в которую надо возвести «а», что бы получить х, называется логарифмом числа х по основанию а.

Основное логарифмическое тождество: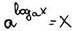

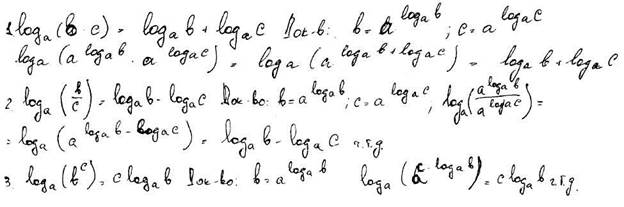
84) Доказать теорему о логарифме числа по основанию а^с.

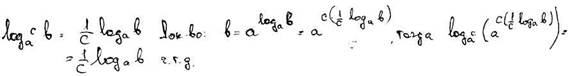
Доказать теорему о переходе к новому основанию. Логарифмическая функция, доказать свойства, построить график.

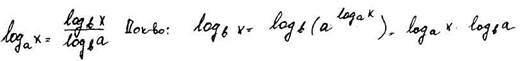
Тригонометрические функции.

Понятие угла. Измерение углов. Направленные углы. Числовая окружность. Соответствие между множеством действительных чисел и мерой угла в радианах. Геометрическая интерпретация тригонометрических функций на координатной окружности.

Угол – это геометрическая фигура, состоящая из 2-х лучей с общим началом, и ограниченной ими плоскостью.

Направленный угол, образуется поворотом луча.

Каждому числу на числовой прямой соответствует радианная мера угла.

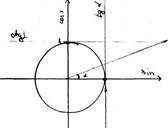
87) Функция синус, доказать её свойства.

88) Функция косинус, доказать её свойства.

89) Функция тангенс, доказать её свойства.

90) Функция котангенс, доказать её свойства.

Доказать основное тригонометрическое тождество и его следствия.

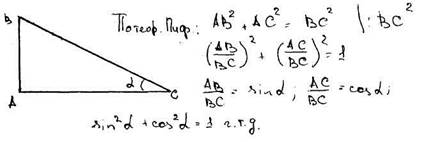
Доказать теоремы сложения. Вывести формулы приведения.

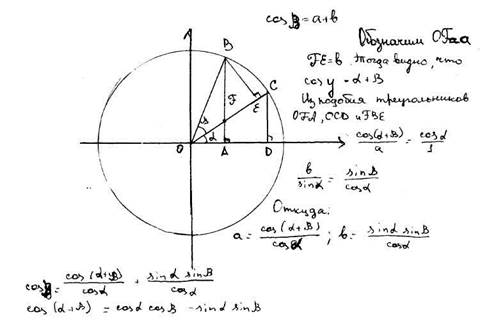
Доказывается через синус и косинус суммы и разности.

Вывести формулы двойных и половинных углов.

Выводится через синус и косинус суммы и разности.

Вывести формулы тригонометрических функций через тангенс половинного угла.

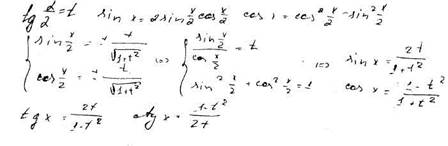
Вывести формулы преобразования суммы тригонометрических функций в произведение и наоборот.

Выводится через синус и косинус суммы и разности.