Означення статистичної гіпотези. Приклади
Серія: теорія ймовірностей та математична статистика
Перевірка статистичних гіпотез
ЛЬВІВ
Уклав: к.ф-м.н., доц. Кінаш О.М.
Відповідальний за випуск: Єлейко Я.І., д.ф.-м. н., проф.
Рецензент:Копитко Б.І., д.ф.-м.н., проф.
Рекомендовано до друку кафедрою теоретичної та прикладної статистики
Протокол № від .
Кінаш О.М. .- Львів: Видавництво ЛНУ, 20 .- 84 с.
© Кінаш О.М.
ЗМІСТ
| 4.1 | Означення статистичної гіпотези. Приклади…………………….. | |
| 4.2 | Критерії узгодження……………………………………………….. | |
| 4.3 | Перевірка гіпотез про розподіл за допомогою критерію c2…….. | |
| 4.3.1 | Критерій c2…………………………………………………………. | |
| 4.3.2 | Нормальний розподіл……………………………………………… | |
| 4.3.3 | Рівномірний розподіл.……………………………………………... | |
| 4.3.4 | Показниковий розподіл.…………………………………………… | |
| 4.3.5 | Розподіл Пуассона.………………………………………………… | |
| 4.3.6 | Біноміальний розподіл..…………………………………………… | |
| 4.3.7 | Перевірка гіпотези про незалежність двох випадкових величин.. | |
| 4.4 | Непараметричні критерії перевірки гіпотез. …………………….. | |
| 4.4.1 | Основні поняття.…………………………………………………… | |
| 4.4.2 | Гіпотеза про однорідність вибірки ……………………………….. | |
| 4.4.3 | Критерій знаків…………………………………………………….. | |
| 4.4.4 | Критерій серій.…………………………………………………….. | |
| 4.4.5 | Перевірка гіпотези про однорідність двох вибірок. Критерій Вілкоксона………………………………………………………….. | |
| 4.4.6 | Двовибірковий критерій узгодження М.В.Смірнова.…………… | |
| 4.4.7 | Критерій Колмогорова.………………………………………….… | |
| 4.5 | Параметричні гіпотези.…………………………………………… | |
| 4.5.1 | Гіпотеза про рівність математичних сподівань двох нормально розподілених ознак генеральної сукупності……………………... | |
| 4.5.2 | Гіпотеза про рівність дисперсій двох нормально розподілених ознак генеральної сукупності…………………………………… | |
| 4.5.3 | Гіпотеза про рівність математичного сподівання 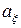 нормально розподіленої ознаки нормально розподіленої ознаки 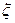 генеральної сукупності гіпотетичному значенню генеральної сукупності гіпотетичному значенню 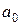 ………………………………………………………... ………………………………………………………... | |
| 4.5.4 | Гіпотеза про рівність дисперсії 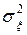 нормально розподіленої ознаки нормально розподіленої ознаки 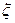 генеральної сукупності гіпотетичному значенню генеральної сукупності гіпотетичному значенню 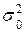 …………………………………………………………………… …………………………………………………………………… | |
| 4.5.5 | Гіпотеза про рівність декількох дисперсій 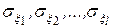 нормально розподілених ознак нормально розподілених ознак 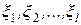 генеральної сукупності за вибірками однакового об'єму.…………………….. генеральної сукупності за вибірками однакового об'єму.…………………….. | |
| 4.5.6 | Гіпотеза про рівність математичних сподівань двох нормально розподілених ознак 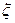 і і 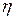 генеральної сукупності з невідомими дисперсіями (залежні вибірки).…………………………………… генеральної сукупності з невідомими дисперсіями (залежні вибірки).…………………………………… | |
| 4.5.7 | Гіпотеза про рівність невідомої ймовірності р гіпотетичній ймовірності 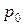 .…………………………………………………….. .…………………………………………………….. | |
| 4.5.8 | Гіпотеза про рівність двох ймовірностей біноміальних розподілів…………………………………………………………… | |
| 4.6 | Застосування ППП………………………………………………… | |
| Додаток……………………………………………………………… | ||
| Література………………………………………………………….. |
Означення статистичної гіпотези. Приклади
Одним з найважливіших і найцікавіших, з професійної точки зору, методом статистичного дослідження властивостей (ознак) генеральної сукупності на основі вибірки у математичній статистиці є метод статистичних гіпотез. Універсальність цього методу полягає в тому, що він дозволяє проводити статистичні дослідження розподілів випадкових величин генеральної сукупності, будувати їх , та знаходити точкові оцінки параметрів цих розподілів.
Означення 4.1. Статистичною гіпотезою називають будь-яке твердження про властивості (ознаки) генеральної сукупності, що перевіряється на основі вибірки. Будемо статистичну гіпотезу позначати через H0.
Її називають нульовою гіпотезою. Поряд із нульовою гіпотезою Н0 розглядають одну із альтернативних (конкуруючих) гіпотез Н1, яка містить відмінне від змісту гіпотези Н0 твердження про ту саму властивість випадкової величини (ознаки) x в генеральній сукупності. Вибір альтернативної гіпотези визначається умовою задачі, яка розглядається.
Приклади конкретних гіпотез.
І. Гіпотеза про розподіл – це твердження про те, що випадкова величина (ознака) x генеральної сукупності, що досліджується, має цей чи інший закон розподілу, функцію розподілу Fx(x) або густину ймовірності fx(x). Математично це записується так:
H0:Fx(x)=g(x), (4.1)
де g(x) - відома функція.
Якщо розподіл випадкової величини x даною гіпотезою задається повністю, то вона називається простою. Вираз (4.1) означає просту гіпотезу. Складною гіпотеза про розподіл називається тоді, коли закон розподілу, функція розподілу або густина ймовірності випадкової величини задається нею з точністю до невідомих параметрів. Наприклад, гіпотеза
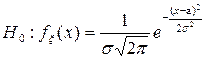
є складною гіпотезою, оскільки невідомими після даного твердження залишаються параметри а і s.
2. Гіпотеза про незалежність – це твердження про те, що дві випадкові величини (ознаки) x і h в генеральній сукупності є незалежними. Математично вона запишеться як:H0: P(x=xi,h=yj)=P(x=xi)P(h=yj), i= 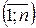 та j=
та j= 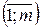 .
.
3. Параметрична гіпотеза – це твердження про те, що деякі параметри розподілу випадкової величини x в генеральній сукупності приймають ті чи інші значення.
Для ілюстрації означення 4.1 ми привели лише три гіпотези. Насправді, їх існує набагато більше.
Відомо, що аксіомою (гіпотезою) називають твердження, яке приймається без доведення. Але слід зауважити, що перед тим, як була прийнята така точка зору, кожна з математичних гіпотез була, як правило, багато разів перевірена на практиці. Тому і будь-яку статистичну гіпотезу необхідно перевірити на практиці з допомогою проведеної вибірки. А вже після цього прийняти рішення про її справедливість. Для цього необхідно побудувати певні критерії узгодження даних, які містяться в гіпотезі, з тими результатами, які отримують при статистичній обробці вибірки. Методику побудови такого типу критеріїв в загальному випадку розглянемо в наступному пункті. Але перед тим домовимося, що інформацію, яка міститься в гіпотезі, будемо називати теоретичною, на відміну від інформації, отриманої на основі вибірки, яку ми назвали емпіричною.
Критерії узгодження
Нехай при статистичному дослідженні даної випадкової величини (ознаки) x в генеральній сукупності провели вибірку (x1, x2, ..., xn) і, виходячи з результатів попередньої вибірки або з інших міркувань, прийняли гіпотезу H0 про одну з її характеристик (про розподіл x або про його параметри). Необхідно на основі вибірки (x1, x2, ..., xn) знайти правило, з допомогою якого можна вирішувати питання про відповідність гіпотези H0 отриманим статистичним даним.
Означення 4.2. Правило, за яким приймається рішення прийняти або відхилити гіпотезу H0, називається критерієм узгодження.
Розглянемо принцип побудови критерію узгодження в загальному випадку.
Найважливішою при вирішенні даної задачі є проблема знаходження для вибірки (x1, x2, ..., xn) випадкової величини (статистики) t=t(x1, x2, ..., xn), котра виражала б міру відхилення теоретичних (отриманих на основі прийняття гіпотези) даних від емпіричних, які отримані на основі вибірки.
Допустимо, що таку випадкову величину (статистику) t=t(x1, x2, ..., xn) знайдено, а область W - множина можливих значень даної випадкової величини. Далі фіксується деяка мала ймовірність a (a<0,1), яка називається рівнем значущості, а область Wa визначається умовою:
P(tÎWa)£ a. (4.2)
Іншими словами, Wa представляє собою таку область, що ймовірність попадання випадкової величини t в Wa не більша від рівня значущості a. Область Wa називається критичною областю. Її знаходять для заданого a, знаючи випадкову величину t, з умови (4.2). Як правило, в практичних застосуваннях критична область Wa представляє собою інтервал виду Wa=(t >ta). Область W\Wa називають областю прийняття гіпотези H0.
Точка ta , яка відділяє критичну область Wa від області прийняття гіпотези W\Wa , називається критичною точкою.
Як правило, в практичних застосуваннях розглядають два типи критичних областей Wa: а) одностороння (лівостороння або правостороння); б) двостороння.
Лівосторонньою називають критичну область Wa=(t <ta), ta<0, причому критична точка ta визначається з умови P(t <ta)= a.
Правосторонньою називають критичну область Wa=(t >ta), ta>0, причому критична точка ta визначається з умови P(t >ta)= a.
Двосторонньою називають критичну область Wa=(t <t 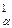 , t >t
, t >t 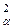 ), t
), t 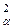 >t
>t 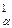 , причому критичні точки t
, причому критичні точки t 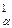 , t
, t 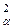 визначаються з умови P(t <t
визначаються з умови P(t <t 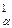 )+P(t >t
)+P(t >t 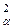 )= a.
)= a.
Зокрема, якщо t 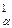 і t
і t 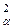 симетричні відносно нуля, то Wa=(
симетричні відносно нуля, то Wa=( 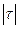 >ta), ta>0, причому ta визначається з умови P(t <-ta)=P(t >ta)=
>ta), ta>0, причому ta визначається з умови P(t <-ta)=P(t >ta)= 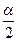 .
.
Якщо рівень значущості a визначає “розмір” критичної області Wa, то положення критичної області на множині значень статистики t залежить від формулювання альтернативної гіпотези Н1.
Наприклад, якщо перевіряється гіпотеза H0: 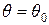 , а альтернативна гіпотеза Н1:
, а альтернативна гіпотеза Н1: 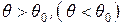 , то критична область розміщується на правому (лівому) “хвості” розподілу статистики t, тобто є правосторонньою (лівосторонньою) критичною областю.
, то критична область розміщується на правому (лівому) “хвості” розподілу статистики t, тобто є правосторонньою (лівосторонньою) критичною областю.
Якщо альтернативна гіпотеза Н1: 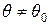 , то критична область розміщується на обох “хвостах” розподілу статистики t, тобто є двосторонньою.
, то критична область розміщується на обох “хвостах” розподілу статистики t, тобто є двосторонньою.
Таким чином, шуканий критерій узгодження формулюється так:
1. Якщо точкова оцінка 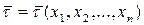 , обчислена на основі вибірки
, обчислена на основі вибірки 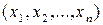 , попадає в критичну область Wa(
, попадає в критичну область Wa( 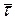 ÎWa), то гіпотезу H0 відхиляють.
ÎWa), то гіпотезу H0 відхиляють.
2. Якщо ж значення 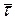 попадає в область прийняття гіпотези W\Wa(
попадає в область прийняття гіпотези W\Wa( 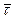 ÎW\Wa), то гіпотезу H0 приймають.
ÎW\Wa), то гіпотезу H0 приймають.
Отже, для перевірки статистичної гіпотези на практиці необхідно:
1. Для висунутої у задачі гіпотези H0 і на основі вибірки 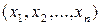 знайти випадкову величину (статистику) t=t(x1, x2, ..., xn).
знайти випадкову величину (статистику) t=t(x1, x2, ..., xn).
2. З умови (4.2) для заданого рівня значущості a визначити критичну область Wa.
3. Для даної вибірки 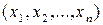 отримати точкову оцінку
отримати точкову оцінку 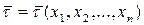 .
.
4. На основі сформульованого вище критерію узгодження прийняти рішення.
Зауваження 4.1. Рішення, яке приймається на основі критерію узгодження, може бути помилковим. Нехай точкова оцінка 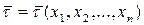 попадає в критичну область Wa і гіпотеза H0 відхиляється у відповідності з критерієм. Якщо ж гіпотеза H0 все-таки вірна, то прийняте рішення помилкове. Помилка, яка здійснюється при відхиленні правильної гіпотези H0, називається помилкою першого роду. Ймовірність помилки першого роду дорівнює ймовірності попадання випадкової величини t в критичну область Wa при умові, що справедлива гіпотеза H0, тобто дорівнює рівню значущості a. Помилка другого роду b наступає в тому випадку, якщо гіпотеза H0 приймається, але, насправді, вона невірна. Простіше можна сказати, що при великій кількості вибірок частка помилкових рішень дорівнює a, якщо гіпотеза H0 вірна, і b, якщо вона невірна. На практиці при проведенні конкретних досліджень необхідно контролювати величини обох помилок як a, так і b. З цією метою розглядають альтернативну гіпотезу H1. Тоді рівняння, які визначають величини помилок першого і другого роду, запишуться у виді:
попадає в критичну область Wa і гіпотеза H0 відхиляється у відповідності з критерієм. Якщо ж гіпотеза H0 все-таки вірна, то прийняте рішення помилкове. Помилка, яка здійснюється при відхиленні правильної гіпотези H0, називається помилкою першого роду. Ймовірність помилки першого роду дорівнює ймовірності попадання випадкової величини t в критичну область Wa при умові, що справедлива гіпотеза H0, тобто дорівнює рівню значущості a. Помилка другого роду b наступає в тому випадку, якщо гіпотеза H0 приймається, але, насправді, вона невірна. Простіше можна сказати, що при великій кількості вибірок частка помилкових рішень дорівнює a, якщо гіпотеза H0 вірна, і b, якщо вона невірна. На практиці при проведенні конкретних досліджень необхідно контролювати величини обох помилок як a, так і b. З цією метою розглядають альтернативну гіпотезу H1. Тоді рівняння, які визначають величини помилок першого і другого роду, запишуться у виді:
P(tÎWa|H0)=a, (4.3)
P(tÎW\Wa|H0)=b, (4.4)
відповідно. Ймовірності в лівих частинах рівнянь розуміють як умовні ймовірності. Як доводиться у математичній статистиці, при заданому об’ємі вибірки відповідний вибір критичної області Wa дозволяє зробити як завгодно малою або помилку a , або помилку b.
Величину 1-a називають надійністю критерію. Надійність критерію є ймовірністю того, що нульова гіпотеза буде прийнятою, якщо хибна альтернативна.
Величину 1-b називають потужністю критерію. Потужність критерію є ймовірністю того, що нульова гіпотеза буде відкинута, якщо вірна альтернативна.
Очевидно, що на множині W значень статистики t критерію можна вибирати як завгодно багато критичних областей Wa для заданого рівня значущості a, проте відповідні їм критерії будуть мати, взагалі кажучи, різні ймовірності помилок другого роду.
Найкращою критичною областю (НКО) називають критичну область, яка для заданого рівня значущості a, забезпечує мінімальну ймовірність помилки другого роду.
Перевірка статистичних гіпотез з використанням критеріїв значущості може бути проведена на основі довірчих інтервалів. Так для всіх параметричних гіпотез область прийняття гіпотези Н0: 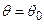 для рівня значущості a співпадає з довірчим інтервалом для параметра
для рівня значущості a співпадає з довірчим інтервалом для параметра 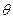 при довірчій ймовірності 1-a. При цьому односторонньому критерію значущості відповідає односторонній довірчий інтервал, а двосторонньому – двосторонній довірчий інтервал. Гіпотеза Н0 приймається, якщо значення
при довірчій ймовірності 1-a. При цьому односторонньому критерію значущості відповідає односторонній довірчий інтервал, а двосторонньому – двосторонній довірчий інтервал. Гіпотеза Н0 приймається, якщо значення 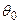 покривається відповідним довірчим інтервалом; в іншому випадку гіпотеза Н0 відхиляється.
покривається відповідним довірчим інтервалом; в іншому випадку гіпотеза Н0 відхиляється.
Якщо перевіряється гіпотеза Н0: 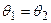 і довірчий інтервал для різниці параметрів
і довірчий інтервал для різниці параметрів 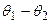 накриває нульове значення, то гіпотеза приймається. Виключення становить перевірка гіпотези про рівність дисперсій, оскільки довірчий інтервал будується для відношення дисперсій. В цьому випадку гіпотеза Н0 приймається, якщо довірчий інтервал накриває значення рівне 1.
накриває нульове значення, то гіпотеза приймається. Виключення становить перевірка гіпотези про рівність дисперсій, оскільки довірчий інтервал будується для відношення дисперсій. В цьому випадку гіпотеза Н0 приймається, якщо довірчий інтервал накриває значення рівне 1.
Перейдемо до розгляду методики перевірки конкретних гіпотез.
4.3. Перевірка гіпотез про розподіл за допомогою критерію 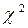
4.3.1. Критерій 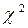
Нехай, досліджуючи деяку випадкову величину (ознаку) x в генеральній сукупності, отримали вибірку 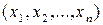 і прийняли таку (просту) гіпотезу про її розподіл:
і прийняли таку (просту) гіпотезу про її розподіл:
H0:Fx(x)=g(x), (4.5)
де g(x) – відома функція. Необхідно для даної гіпотези побудувати критерій узгодження.
Згідно із загальною схемою перевірки статистичних гіпотез, яка наведена у попередньому параграфі, першим її етапом є знаходження випадкової величини (статистики) t=t(x1, x2, ..., xn). Для цього проаналізуємо емпіричні і теоретичні дані.
Вважатимемо, що ми провели статистичну обробку заданої вибірки (x1, x2, ..., xn) згідно з методикою і отримали інтервальну таблицю частот типу
| [zi-1,zi) | [z0,z1) | [z1,z2) | . . . . . |
| ||||
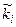 | 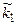 | 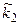 | . . . . . | 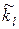 |
де 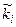 - будемо називати також емпіричними частотами. Нагадаємо, що
- будемо називати також емпіричними частотами. Нагадаємо, що 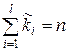 .
.
Нами уже підкреслювалось, що інтервальна таблиця частот (4.6) або відповідна інтервальна таблиця відносних частот представляють емпіричний закон розподілу випадкової величини x, що досліджується в генеральній сукупності. Зокрема, на основі цих таблиць можна знайти емпіричну функцію розподілу 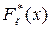 .З іншого боку, виходячи зі змісту прийнятої гіпотези (4.5), можна зробити висновок, що після її прийняття повністю відомий розподіл випадкової величини x, що досліджується. А отже, можемо знайти і, так звані, теоретичні частоти
.З іншого боку, виходячи зі змісту прийнятої гіпотези (4.5), можна зробити висновок, що після її прийняття повністю відомий розподіл випадкової величини x, що досліджується. А отже, можемо знайти і, так звані, теоретичні частоти 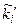 , які означають, скільки елементів вибірки попало би в інтервал [zi-1, zi), якби функція розподілу Fx(x) випадкової величини x співпадала з функцією розподілу означеною в гіпотезі H0.
, які означають, скільки елементів вибірки попало би в інтервал [zi-1, zi), якби функція розподілу Fx(x) випадкової величини x співпадала з функцією розподілу означеною в гіпотезі H0.
Насправді, скориставшись формулою 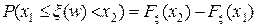 , на основі гіпотези H0 знайдемо ймовірності pi попадання даної випадкової величини x в інтервал [zi-1, zi). Будемо мати:
, на основі гіпотези H0 знайдемо ймовірності pi попадання даної випадкової величини x в інтервал [zi-1, zi). Будемо мати:
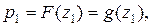
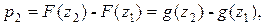 ....... ,
....... , 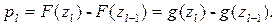
Звідси, на основі статистичного означення ймовірності для теоретичних частот 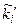 дістанемо, що
дістанемо, що 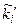 =npi, i=1, 2, ..., l. Це дає можливість побудувати теоретичний закон розподілу у вигляді наступної інтервальної таблиці:
=npi, i=1, 2, ..., l. Це дає можливість побудувати теоретичний закон розподілу у вигляді наступної інтервальної таблиці:
| [zi-1,zi) | [z0,z1) | [z1,z2) | . . . |
| ||
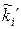 | 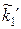 | 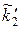 | . . . | 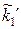 |
де теоретичні частоти 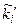 також задовольняють умову
також задовольняють умову 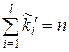 .
.
За міру відхилення теоретичного розподілу (4.7) від емпіричного (4.6.) вибирають таку випадкову величину (статистику):
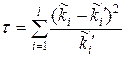 . (4.8)
. (4.8)
Найважливіше є те, що для випадкової величини (4.8) відомий розподіл, який знайдений К.Пірсоном. А саме, справедлива теорема, яку ми наводимо без доведення.
Теорема 4.1. Якщо 0<pi<1, i=1, 2, ..., l, то асимптотично (при 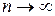 ) випадкова величина t (4.8) має c2 - розподіл з k=l-1 ступенями свободи.
) випадкова величина t (4.8) має c2 - розподіл з k=l-1 ступенями свободи.
Саме цей факт дозволяє збудувати критерій узгодження гіпотези H0 для даного випадку. Дійсно, вибравши критичну область Wa у виді (t > ta;k) і, задаючись рівнем значущості a, умову (4.2) можна записати у вигляді:
P(t > ta;k)=a. (4.9)
Випадкова величина t згідно теореми 4.1 має c2 - розподіл. Розв’язавши рівняння (4.9), і знаючи a і k=l-1- число ступенів свободи, за таблицею 5 у додатку для даного розподілу отримаємо, що ta;k=c2a;l-1.
Таким чином, ми знайшли, що у даному випадку критична область буде мати вигляд: Wa=(t > c2a;l-1). Це дозволяє сформулювати шуканий критерій узгодження.
А саме, нехай 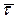 , обчислена за формулою (4.8) на основі таблиць (4.7) і (4.6), точкова оцінка випадкової величини t. Тоді:
, обчислена за формулою (4.8) на основі таблиць (4.7) і (4.6), точкова оцінка випадкової величини t. Тоді:
1. Якщо 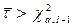 , то гіпотеза H0 відхиляється;
, то гіпотеза H0 відхиляється;
2. Якщо ж 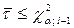 , то гіпотеза H0 приймається.
, то гіпотеза H0 приймається.
Даний критерій узгодження називають критерієм c2 або критерієм Пірсона.
Зауваження 4.2. Розглянемо випадок складної гіпотези про розподіл:
H0:Fx(x)=g(x,Q1,...,Qm), (4.10)
тобто, приймаємо, що розподіл випадкової величини (ознаки) x в генеральній сукупності відомий з точністю до значень невідомих параметрів (Q1, Q2, .., Qm), точкові оцінки яких можна знайти, наприклад, методом максимальної правдоподібності або методом моментів. Побудова критерію узгодження для даної задачі проводиться аналогічно, як і в попередньому випадку, оскільки випадкова величина t (4.8) у даному випадку, як показано, наприклад, в [6], також при 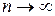 має c2 -розподіл, але з k=l-1–m числом ступенів свободи, де m – число невідомих параметрів. Отже, критична область Wa=(t>ta;k) також визначається розв’язуванням рівняння (4.9) для заданого рівня значущості a і числа ступенів свободи k=l-1-m. Отримаємо розв’язок ta,k=c2a;l-1-m. Тому критерій c2 для даного випадку сформулюється таким чином.
має c2 -розподіл, але з k=l-1–m числом ступенів свободи, де m – число невідомих параметрів. Отже, критична область Wa=(t>ta;k) також визначається розв’язуванням рівняння (4.9) для заданого рівня значущості a і числа ступенів свободи k=l-1-m. Отримаємо розв’язок ta,k=c2a;l-1-m. Тому критерій c2 для даного випадку сформулюється таким чином.
Нехай 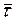 , обчислена за формулою (4.8) на основі таблиць (4.6) і (4.7), - точкова оцінка випадкової величини t. Тоді:
, обчислена за формулою (4.8) на основі таблиць (4.6) і (4.7), - точкова оцінка випадкової величини t. Тоді:
1. Якщо 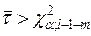 , то гіпотеза H0 відхиляється;
, то гіпотеза H0 відхиляється;
2. Якщо 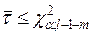 , то гіпотеза H0 приймається.
, то гіпотеза H0 приймається.
Критерієм c2 можна користуватися, коли n – об’єм вибірки та pi, 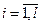 – ймовірності потрапляння вибіркових значень в і-ий інтервал, обчислені за гіпотетичним розподілом є такі, що
– ймовірності потрапляння вибіркових значень в і-ий інтервал, обчислені за гіпотетичним розподілом є такі, що 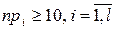 . Поділ інтервалу вибіркових значень здійснюють, взагалі кажучи, довільно, але кількість інтервалів намагаються взяти якомога більше, дотримуючись при цьому вимоги
. Поділ інтервалу вибіркових значень здійснюють, взагалі кажучи, довільно, але кількість інтервалів намагаються взяти якомога більше, дотримуючись при цьому вимоги 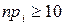 . Якщо при цьому поділі для деяких інтервалів значення
. Якщо при цьому поділі для деяких інтервалів значення 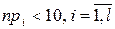 , то такі інтервали слід об’єднати з іншими, так щоб для нових інтервалів
, то такі інтервали слід об’єднати з іншими, так щоб для нових інтервалів 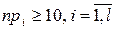 , або щоб вони містили принаймні по 10 вибіркових значень. Якщо вибіркових значень так мало, що цього зробити не можна, то застосовувати критерій c2 із використанням таблиць c2 – розподілу не рекомендується.
, або щоб вони містили принаймні по 10 вибіркових значень. Якщо вибіркових значень так мало, що цього зробити не можна, то застосовувати критерій c2 із використанням таблиць c2 – розподілу не рекомендується.
В цьому випадку для визначення близькості емпіричного розподілу, наприклад, до нормального користуються числами Вестергарда: 0,3; 0,7; 1,1; 3.
Вважається, що емпіричний розподіл є нормальним, якщо:
1) на інтервалі 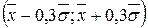 міститься
міститься 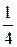 всієї сукупності;
всієї сукупності;
2) на інтервалі 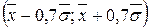 міститься
міститься 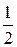 всієї сукупності;
всієї сукупності;
3) на інтервалі 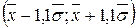 міститься
міститься 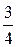 всієї сукупності;
всієї сукупності;
4) на інтервалі 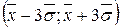 міститься 0,998 всієї сукупності.
міститься 0,998 всієї сукупності.
Зауваження 4.3. Недоліком даного методу перевірки гіпотез про розподіл є те, що при побудові інтервальної таблиці частот втрачається деяка частина інформації. Крім цього, залишається відкритим питання про вибір числа інтервалів l і їх довжини. При перевірці гіпотези про розподіл даним методом контролюється лише похибка першого роду. Однак, критерій c2 має і деякі переваги: а) при його застосуванні нема необхідності враховувати точні значення вибіркових спостережень; б) він універсальний стосовно природи випадкової величини (ознаки), що досліджується.
Нормальний розподіл
а) емпіричний розподіл заданий у виді рівновіддалених варіант.
Для заданого рівня значущості a перевірку гіпотези про нормальний закон розподілу генеральної сукупності проводять за схемою:
1. Обчислюємо вибіркове середнє 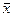 і вибіркове середнє квадратичне відхилення
і вибіркове середнє квадратичне відхилення 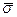 .
.
2. Теоретичні частоти 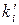 обчислюємо за формулою
обчислюємо за формулою 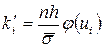 , де n – об’єм вибірки, h – різниця між двома сусідніми варіантами (крок),
, де n – об’єм вибірки, h – різниця між двома сусідніми варіантами (крок), 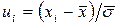 ,
, 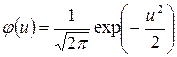 .
.
3. Критична область 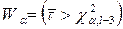 , де
, де 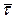 – точкова оцінка випадкової величини
– точкова оцінка випадкової величини 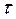 ,
, 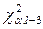 – критична точка правосторонньої критичної області, яку для заданого рівня значущості a і числа ступенів свободи
– критична точка правосторонньої критичної області, яку для заданого рівня значущості a і числа ступенів свободи 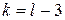 знаходять за таблицею 5 у додатку.
знаходять за таблицею 5 у додатку.
Зауваження 4.4. Якщо в окремих розрядах емпіричні частоти малочисельні (ki < 10), то їх об’єднують, а відповідні їм емпіричні та теоретичні частоти додають. Тоді при обчисленні число ступенів свободи l дорівнює числу розрядів вибірки, які залишились після об’єднання.
Зауваження 4.5. Для контролю за правильністю обчислень користуються рівністю
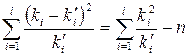 .
.
б) емпіричний розподіл заданий у виді послідовності інтервалів (xi, xi+1) і відповідних їм частот 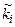 .
.
Нехай рівень значущості a задано. Тоді:
1. Обчислюємо 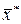 і
і 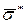 , причому
, причому 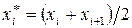 .
.
2. Переходимо до випадкової величини 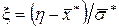 і шукаємо кінці інтервалів за формулами
і шукаємо кінці інтервалів за формулами 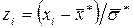 ,
, 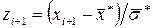 , причому найменше z покладаємо рівним -¥, а найбільше +¥.
, причому найменше z покладаємо рівним -¥, а найбільше +¥.
3. Теоретичні частоти 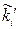 обчислюємо за формулою
обчислюємо за формулою 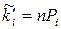 , де n – об’єм вибірки,
, де n – об’єм вибірки, 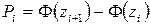 – ймовірності попадання випадкової величини x в інтервал (xi, xi+1),
– ймовірності попадання випадкової величини x в інтервал (xi, xi+1), 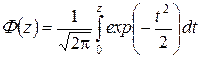 .
.
4. Критична область 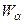 визначається аналогічно до пункту а).
визначається аналогічно до пункту а).
Тут і надалі (п.п. 2, 3, 4, 5) слід враховувати також зауваження 4.6 і 4.7.
Приклад 4.1. Групування споживчих товариств (СТ) за величиною роздрібного товарообігу дало наступні результати:
| Групи СТ (тис. грн.) | [zi, zi+1) | [0 – 100) | [100 – 200) | [200 – 300) | [300 – 400) | [400 – 500] |
| Кількість СТ | 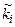 |
Для рівня значущості a=0,05 перевірити гіпотезу про нормальність розподілу генеральної сукупності.
Розв’язок. Перейдемо від інтервальної таблиці частот до статистичного ряду з рівновіддаленими варіантами, поклавши 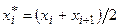 :
:
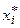 | |||||
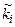 |
Для нього 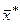 = 186,36,
= 186,36, 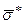 = 115,87.
= 115,87.
Обчислюємо теоретичні частоти 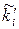 . Для цього складаємо розрахункову таблицю 4.1.
. Для цього складаємо розрахункову таблицю 4.1.
Таблиця 4.1
| i | xi | xi+1 | 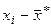 | 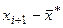 | 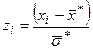 | 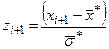 | 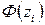 | 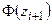 | 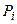 | 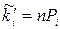 |
| -186,36 | -86,36 | -¥ | -0,7453 | -0,5 | -0,27337 | 0,22663 | 44,83 | |||
| -86,36 | 13,64 | -0,7453 | 0,1177 | -0,27337 | 0,04776 | 0,32113 | 63,58 | |||
| 13,64 | 113,64 | 0,1177 | 0,9808 | 0,04776 | 0,33648 | 0,28872 | 57,17 | |||
| 113,64 | 213,64 | 0,9808 | 1,8438 | 0,33648 | 0,46712 | 0,13064 | 25,87 | |||
| 213,64 | 313,64 | 1,8438 | +¥ | 0,46712 | 0,5 | 0,03288 | 6,51 | |||
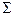 | 197,96 |
Порівняємо емпіричні і теоретичні частоти і проведемо контроль обчислень (зауваження 4.7). Складемо таблицю 4.2.
Таблиця 4.2
| i | 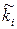 | 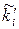 | 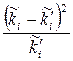 | 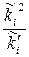 |
| 44,83 | 7,9 | 15,079 | ||
| 63,58 | 23,22 | 163,636 | ||
| 57,17 | 1,47 | 40,301 | ||
| 25,87 | 3,77 | 9,896 | ||
| 6,51 | 0,004 | 5,530 | ||
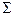 | 36,364 | 234,442 |
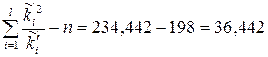 .
.
Оскільки незначна різниця між 36,442 і 36,364 зумовлена заокругленнями при проведенні обчислень, то можемо вважати, що вони проведені вірно. З таблиці 5 у додатку знаходимо, що 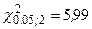 . Враховуючи, що 36,364 > 5,99, то гіпотеза про нормальність розподілу відхиляється. Це означає, що дані досліджень не узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності.
. Враховуючи, що 36,364 > 5,99, то гіпотеза про нормальність розподілу відхиляється. Це означає, що дані досліджень не узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності.
Рівномірний розподіл
Емпіричний розподіл неперервної випадкової величини заданий у виді послідовності інтервалів (xi-1, xi), і відповідних їм частот 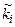 ,
, 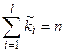 – об’єм вибірки. Для заданого рівня значущості a за допомогою критерію
– об’єм вибірки. Для заданого рівня значущості a за допомогою критерію 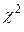 перевірку гіпотези про те, що випадкова величина x розподілена рівномірно, проводять за схемою:
перевірку гіпотези про те, що випадкова величина x розподілена рівномірно, проводять за схемою:
1. Обчислюємо 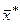 і
і 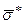 , причому
, причому 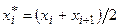 .
.
2. Параметри а* і b* – кінці інтервалу, в якому спостерігаються можливі значення випадкової величини x, оцінюються за формулами: 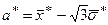 ,
, 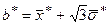 .
.
3. Густина емпіричного розподілу 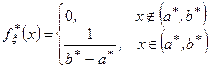 .
.
4. Теоретичні частоти 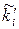 рівні:
рівні:
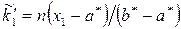 ,
,
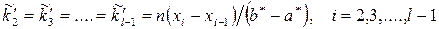 ,
,
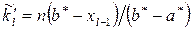 .
.
5. Критична область 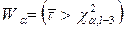 , де
, де 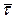 – точкова оцінка випадкової величини
– точкова оцінка випадкової величини 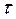 (4.8),
(4.8), 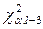 знаходять за таблицею 5 у додатку.
знаходять за таблицею 5 у додатку.
Приклад 4.2. Протягом 5 годин реєстрували відвідування студентами консультацій в сесійний період на кафедрах одного факультету і стримали наступний емпіричний розподіл:
| (zi-1,zi) | [12 – 13) | [13 – 14) | [14 – 15) | [15 – 16) | [16 – 17] |
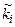 |
Для рівня значущості a=0,01 перевірити гіпотезу про те, що час відвідування студентами консультацій розподілений рівномірно.
Розв’язок. Із заданої інтервальної таблиці частот, поклавши 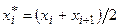 , перейдемо до статистичного ряду з рівновіддаленими варіантами:
, перейдемо до статистичного ряду з рівновіддаленими варіантами:
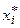 | 12,5 | 13,5 | 14,5 | 15,5 |
| ||
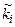 |
Для отриманого ряду обчислимо 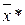 і
і 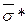 :
:
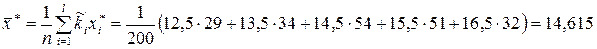 ,
,

звідки 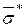 =1,28. Тоді
=1,28. Тоді 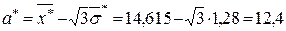 ,
, 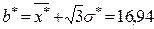 ,
, 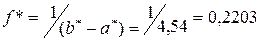 .
.
Теоретичні частоти 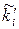 ,
, 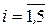 знайдемо за формулами:
знайдемо за формулами:
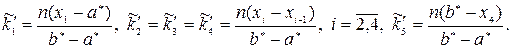
Маємо: 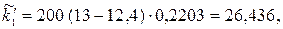
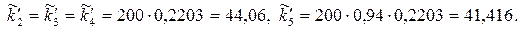
Тоді з формули (4.8) отримаємо:
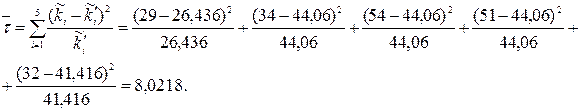
За таблицею 5 у додатку для рівня значущості 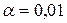 і числом ступенів свободи
і числом ступенів свободи 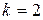 знаходимо
знаходимо 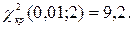 Оскільки
Оскільки 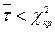 , то гіпотезу про рівномірний розподіл генеральної сукупності приймаємо. Тобто на 99 % можемо стверджувати, що студенти даного факультету рівномірно відвідують консультації в проміжку часу з 12 00 до 17 00.
, то гіпотезу про рівномірний розподіл генеральної сукупності приймаємо. Тобто на 99 % можемо стверджувати, що студенти даного факультету рівномірно відвідують консультації в проміжку часу з 12 00 до 17 00.
Показниковий розподіл
Емпіричний розподіл неперервної випадкової величини заданий у виді послідовності інтервалів (xi-1-xi) і відповідних їм частот 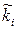 . Для заданого рівня значущості
. Для заданого рівня значущості 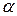 за допомогою критерію
за допомогою критерію 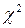 перевірку гіпотези про те, що випадкова величина
перевірку гіпотези про те, що випадкова величина 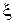 має показниковий розподіл, проводять за схемою:
має показниковий розподіл, проводять за схемою:
1. Обчислюємо 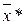 , причому
, причому 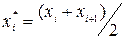 .
.
2. Оцінка параметра 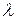 рівна
рівна 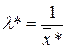 .
.
3. Теоретичні частоти 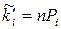 , n – об’єм вибірки,
, n – об’єм вибірки,
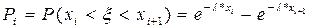 .
.
4. Критична область 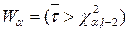 , де
, де 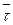 - точкова оцінка випадкової величини
- точкова оцінка випадкової величини 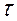 (4.8),
(4.8), 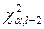 знаходять за таблицею 5 у додатку.
знаходять за таблицею 5 у додатку.
Приклад 4.3. Досліджували неперервний стаж роботи працівників деякого підприємства і отримали наступні результати:
| [хi-1,хi) | [0,10) | [10,20) | [20,30) | [30,40] |
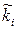 |
де [хi-1,хi)– напівінтервали в роках, 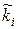 - кількість працівників, величина стажу яких попадає в даний інтервал.
- кількість працівників, величина стажу яких попадає в даний інтервал.
Для рівня значущості 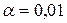 перевірити гіпотезу про те, що величина неперервного стажу має показниковий закон розподілу.
перевірити гіпотезу про те, що величина неперервного стажу має показниковий закон розподілу.
Розв’язок. Згідно з умовою задачі необхідно перевірити наступну гіпотезу:
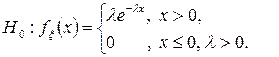
Методом максимальної правдоподібності легко отримати, що точкова оцінка 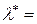
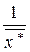 , де
, де 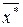 знайдемо в таблиці
знайдемо в таблиці
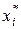 |
| |||||
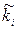 |
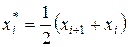 .
.
Маємо: 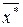 =
= 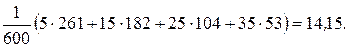 Тоді
Тоді
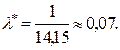
Обчислимо теоретичні частоти 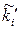 . Для цього складемо таблицю
. Для цього складемо таблицю
| i | xi | xi+1 | 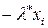 | 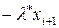 | 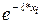 | 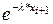 | 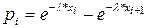 | 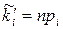 |
| -0,7 -1,4 -2,1 | -0,7 -1,4 -2,1 -2,8 | 0,4966 0,2466 0,1311 | 0,4966 0,2466 0,1311 0,0491 | 0,5044 0,25 0,1155 0,0491 | 326,4 69,3 49,2 |
Звідси і з формули (4.8) отримаємо
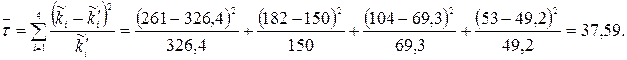 За таблицею 5 у додатку знаходимо
За таблицею 5 у додатку знаходимо 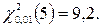 Оскільки 37,59>9,2, то гіпотезу про показниковий розподіл відхиляємо.
Оскільки 37,59>9,2, то гіпотезу про показниковий розподіл відхиляємо.
Розподіл Пуассона
Емпіричний розподіл дискретної випадкової величини заданий у виді статистичного ряду. Для заданого рівня значущості 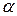 за допомогою критерію
за допомогою критерію 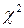 перевірку гіпотези про те, що випадкова величина
перевірку гіпотези про те, що випадкова величина 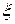 має розподіл Пуассона, проводять за схемою:
має розподіл Пуассона, проводять за схемою:
1. Обчислюємо 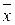 .
.
2. Оцінка параметра 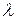 рівна
рівна 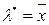 .
.
3. Теоретичні частоти 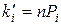 , n – об’єм вибірки, Pi знаходять за формулою Пуассона
, n – об’єм вибірки, Pi знаходять за формулою Пуассона 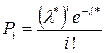 , або за таблицею 3 у додатку.
, або за таблицею 3 у додатку.
4. Критична область 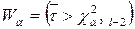 , де
, де 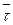 - точкова оцінка випадкової величини
- точкова оцінка випадкової величини 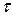 (4.8),
(4.8), 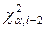 знаходять за таблицею 5 у додатку.
знаходять за таблицею 5 у додатку.
Приклад 4.4. Нехай проведено дослідження про відмову в роботі деякої апаратури за 10000 год. Отримані результати представляються у вигляді такої таблиці частот:
| xi |
| ||||||||
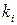 |
де xi - число відмов, а 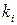 - частота цього числа. Перевірити гіпотезу про те, що число відмов має розподіл Пуассона, якщо рівень значущості a=0,01.
- частота цього числа. Перевірити гіпотезу про те, що число відмов має розподіл Пуассона, якщо рівень значущості a=0,01.
Розв’язок. Згідно умови задачі необхідно перевірити наступну гіпотезу:
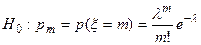 . (4.12)
. (4.12)
Методом максимальної правдоподібності ми отримали, що точкова оцінка l дорівнює вибірковому середньому 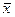 . Для даної вибірки знайдемо, що
. Для даної вибірки знайдемо, що
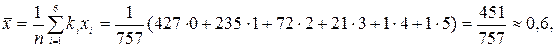
отже, оцінка 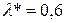 .
.
Для даного 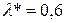 і m=0, 1, 2, 3, 4, 5 за таблицею 3 у додатку для розподілу Пуассона отримаємо теоретичні ймовірності
і m=0, 1, 2, 3, 4, 5 за таблицею 3 у додатку для розподілу Пуассона отримаємо теоретичні ймовірності
p0=P(x=0)=0,54; p1=P(x=1)=0,33; p2=P(x=2)=0,1; p3=P(x=3)=0,02; p4=P(x=4)=0,002; p5=P(x=5)=0.
Звідси, на основі співвідношення 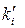 =npi,i = 0, 1, 2, 3, 4, 5 визначимо теоретичні частоти:
=npi,i = 0, 1, 2, 3, 4, 5 визначимо теоретичні частоти: 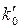 =416,
=416, 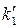 =249,
=249, 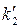 =75,
=75, 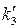 =17,
=17, 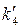 =2,
=2, 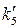 =0.
=0.
Зауважимо, що не зменшуючи загальності викладу, ми вдалися до заокруглень величин pi і 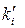 .Тепер, використовуючи формулу (4.8), на основі заданої таблиці частот і знайдених теоретичних частот, знайдемо точкову оцінку
.Тепер, використовуючи формулу (4.8), на основі заданої таблиці частот і знайдених теоретичних частот, знайдемо точкову оцінку 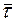 . Будемо мати:
. Будемо мати:
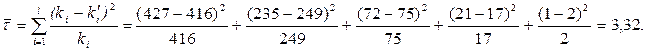 За таблицею 5 у додатку для c2 - розподілу для a=0,01 і числа ступенів свободи k=l-1-m=5-1-1=3 розв’яжемо рівняння (4.9). Отримаємо, що ta;k=c20,01;3=9,5.
За таблицею 5 у додатку для c2 - розподілу для a=0,01 і числа ступенів свободи k=l-1-m=5-1-1=3 розв’яжемо рівняння (4.9). Отримаємо, що ta;k=c20,01;3=9,5.
Оскільки 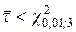 , то згідно з критерієм c2, який сформульований у зауваженні 4.2, дана гіпотеза (4.12) може бути прийнятою.
, то згідно з критерієм c2, який сформульований у зауваженні 4.2, дана гіпотеза (4.12) може бути прийнятою.
Біноміальний розподіл
Проведено n дослідів, кожний з яких складається з m незалежних випробувань з однаковою ймовірністю появи події А. Емпіричний закон розподілу дискретної випадкової величини 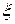 =(число появ події А) задається у вигляді статистичного ряду
=(число появ події А) задається у вигляді статистичного ряду
| xi | … |
| |||||
| ki | k0 | k1 | k2 | kl |
Для заданого рівня значущості 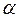 за допомогою критерію
за допомогою критерію 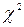 перевірку гіпотези про те, що випадкова величина
перевірку гіпотези про те, що випадкова величина 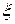 має біноміальний розподіл проводять за схемою:
має біноміальний розподіл проводять за схемою:
1. Теоретичні частоти 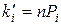 , n – число дослідів, Pi – ймовірність появи i подій A в m випробуваннях
, n – число дослідів, Pi – ймовірність появи i подій A в m випробуваннях 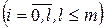 , знаходять за формулою Бернуллі
, знаходять за формулою Бернуллі 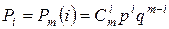 .( табл.15 у додатку)
.( табл.15 у додатку)
2. Критична область 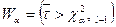 , де
, де 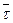 - точкова оцінка випадкової величини
- точкова оцінка випадкової величини 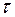 (4.8),
(4.8), 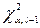 знаходять за таблицею 5 у додатку.
знаходять за таблицею 5 у додатку.
Зауваження 4.6. Якщо ймовірність появи події A в кожному випробуванні не задана, то її оцінюють відносною частотою або методом максимальної правдоподібності за формулою 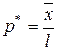 . Тоді число ступенів вільності k=l-2 і замість
. Тоді число ступенів вільності k=l-2 і замість 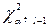 потрібно шукати
потрібно шукати 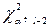 .
.
Приклад 4.5. Серед 193 дводітних сімей, які проживають на території даної сільської ради, 45 мають двох хлопчиків, 53 – двоє дівчаток, у 95 – діти різної статі. Чи можна вважати, що кількість дівчаток у сім’ї, яка має двох дітей, є біноміально розподіленою випадковою величиною? Взяти 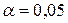 .
.
Розв’язок. Випадкова величина 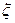 ={кількість дівчаток у дводітній сім’ї} набуває значень 0, 1, 2. Параметр p гіпотетичного розподілу невідомий. Оцінимо його за вибіркою
={кількість дівчаток у дводітній сім’ї} набуває значень 0, 1, 2. Параметр p гіпотетичного розподілу невідомий. Оцінимо його за вибіркою 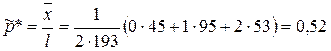 . Тоді
. Тоді 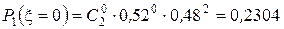 ,
, 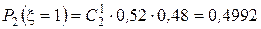 ,
, 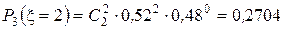 .
.
