Определение линейного оператора и его простейшие свойства. Теорема о существовании линейного оператора

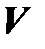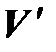Определение. Пусть и – линейные пространства над одним и тем же полем 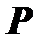. Отображение 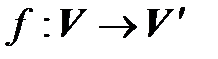называется линейным оператором, если оно удовлетворяет следующим условиям:

1*.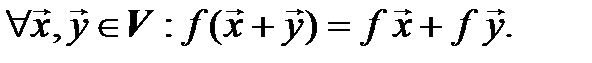

2*.

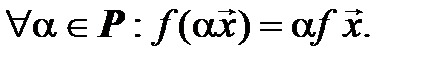
Следствие. При линейном операторе образ линейной комбинации векторов равен такой же линейной комбинации их образов, т. е. если 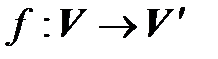– линейный оператор, то :

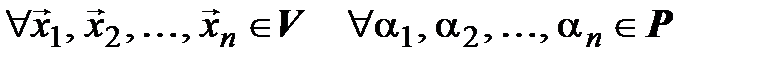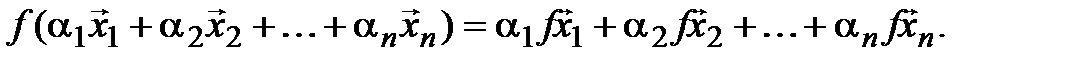(4.3)

uДоказательство проведем методом математической индукции по количеству векторов.

а) n = 1: 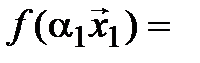[2*] 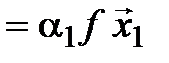– истинно.

б) Предполагая, что утверждение верно для (n-1)-го вектора, доказываем его для n векторов.

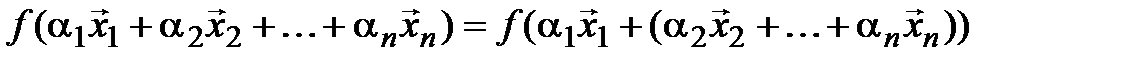= [1*] =

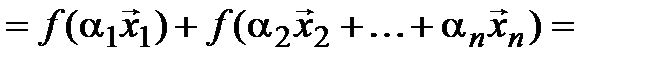[2* и предположение индукции] =

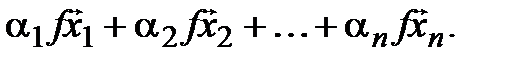= t

Примеры линейных операторов

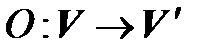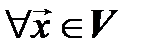
1. Нулевой оператор : 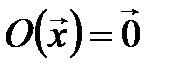. Очевидно, этот оператор удовлетворяет условиям 1* и 2*, значит, является линейным.

2. Тождественный оператор 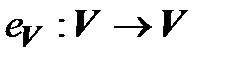также, очевидно, является линейным.

3. Оператор дифференцирования 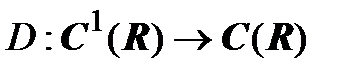, который каждой дифференцируемой функции ставит в соответствие ее производную, является линейным, так как производная суммы функций равна сумме их производных, а при умножении функции на число ее производная умножается на это число.

4. Пусть 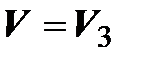– пространство свободных векторов,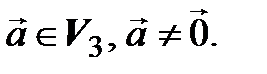

Покажем, что оператор проектирования на ось 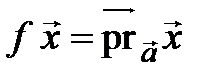является линейным.

►В аналитической геометрии доказывалось, что 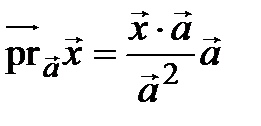. Тогда

: = = = = ;

: = = =

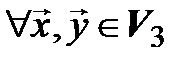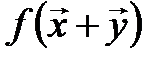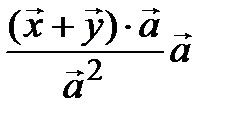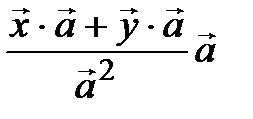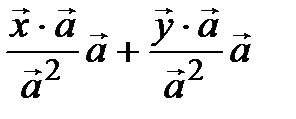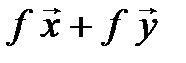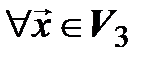
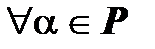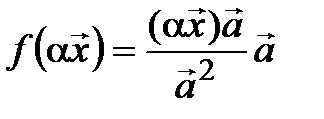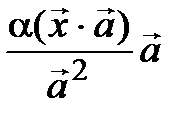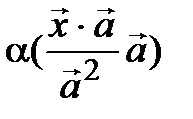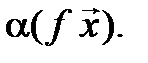
Таким образом, условия 1* и 2* выполняются, а значит, оператор проектирования вектора на ось является линейным.◄

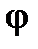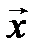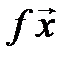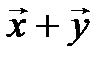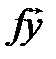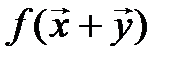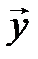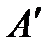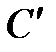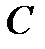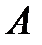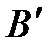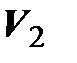5. В пространстве векторов плоскости, закрепленных в начале координат О, рассмотрим оператор 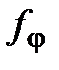поворота вектора на угол 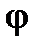против часовой стрелки и докажем его линейность.

► Пусть 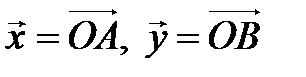– произвольные векторы,

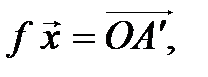
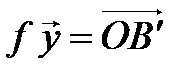(рис. 4.4), 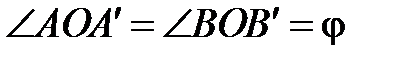. Построим 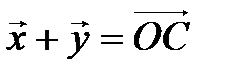и 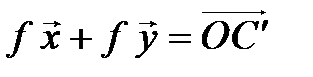по правилу параллелограмма. Так как плоскость поворачивается

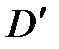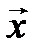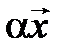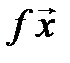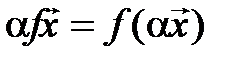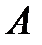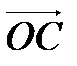Рис.4.4 как жесткое целое, методами элементарной геометрии нетрудно показать, что при этом повороте диагональ переходит в диагональ 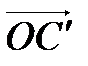. Значит, .

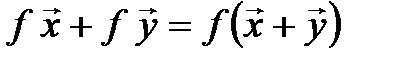Рис. 4.5

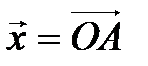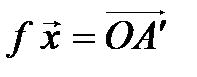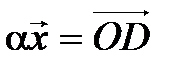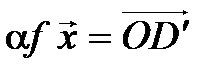Пусть , , , , (рис.4.5). Очевидно, вектор 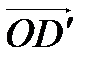получен из 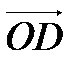поворотом на угол 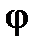, следовательно, 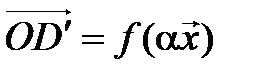, а значит, 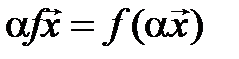. Аналогично это свойство проверяется и при 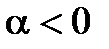, а при 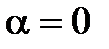оно очевидно.◄

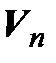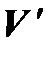Теорема 4.1. Пусть и – линейные пространства над одним и тем же полем P и пусть в пространстве 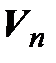задан базис

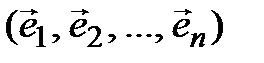, (4.4)

а в пространстве 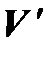– произвольная система векторов

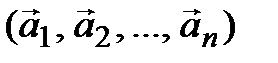. (4.5)

Тогда существует единственный линейный оператор 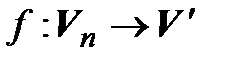, переводящий базис (4.4) в систему (4.5), то есть такой, что

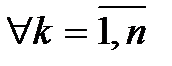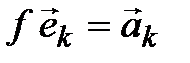: . (4.6)

►Построение. Выберем произвольный вектор 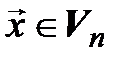и разложим его по базису (4.4): 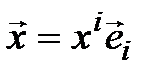. Положим по определению

.

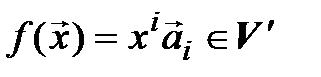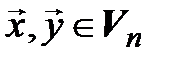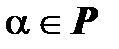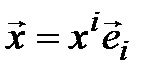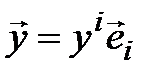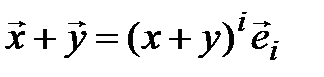
Линейность. Если – произвольные векторы, , то , , , 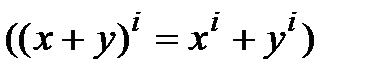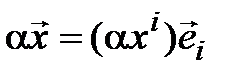. Тогда

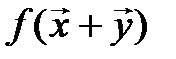= [определение f] = ;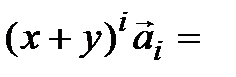

.

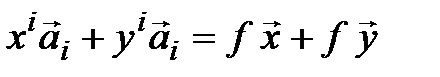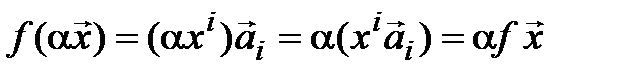Выполнение (4.6). Заметим, что все координаты вектора 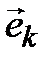в базисе (4.3) равны нулю, за исключением k-й, которая равна 1. Таким образом, i-я координата вектор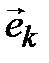а равна 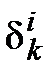, то есть 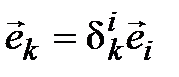. Тогда

,

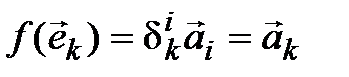значит, условие (4.6) выполнено.

Единственность. Предположим, что существует еще один линейный оператор 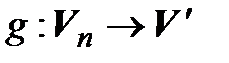, , 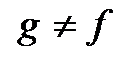переводящий (4.4) в (4.5), то есть такой, что 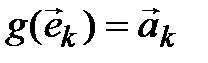. Тогда : 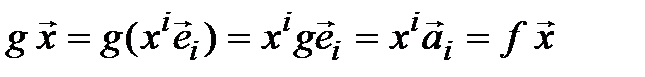– противоречие.◄