Движение поезда при торможении и выбеге

Выбег

Выбег, или движение накатом, – это движение поезда с отключенными тяговыми двигателями и без применения тормозов. Применяется для гашения скорости поезда перед режимом активного торможения. В этом случае происходит уменьшение кинетической энергии поезда, которая в режиме торможения превращается в теплоту, выделяемую на тормозных колодках и колесах.

В режиме выбега на поезд в направлении рельсов действуют сила сопротивления качению колес μ_сопр M g и скатывающая сила M g i. Уравнение второго закона Ньютона для поезда в проекции на направление ускорения (то есть против вектора скорости) примет вид M a = (μ_сопр+i) M g. Из этого выражения видно, что ускорение в режиме выбега постоянно и не зависит от массы поезда

a = (μ_сопр+i) g. (4.13)

Если выбег происходит на крутом спуске (i<0), то скатывающая сила может оказаться больше, чем сила сопротивления, и скорость поезда будет возрастать. В этом случае режим выбега будет невозможен.

Торможение

Режим торможения является важнейшим в обеспечении безопасности движения. От выбранного режима зависит жизнь людей, сохранность грузов и подвижного состава и точность остановки поезда в назначенном месте в назначенное время.

Определим ускорение поезда при торможении всеми колесами поезда. На поезд при торможении действуют следующие силы: со стороны Земли – сила тяжести поезда Мg, включая силу тяжести локомотива mg;со стороны рельсов – касательныесила торможения F_торм всех вагонов и локомотива и сила сопротивления качению поезда F_сопр; нормально со стороны рельсов действуетсила нормального давления на колеса локомотива и состава N (рис. 4.3). Внутренние силы в автосцепках между вагонами действуют попарно, взаимно компенсируются и на движение влияния не оказывают.

Уравнение второго закона Ньютона для процесса торможения поезда в векторной форме имеет вид: произведение массы поезда на ускорение равно векторной сумме всех внешних сил:

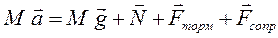. (4.14)

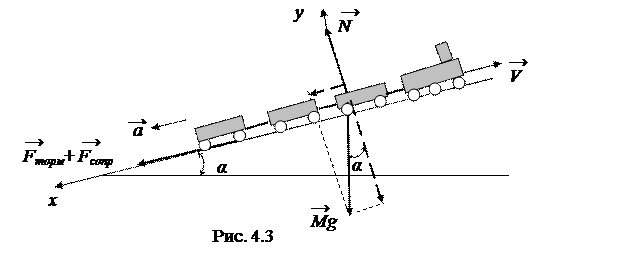
В проекции на координатную ось Ох, направленную вдоль рельсов по ускорению (против хода поезда) и на ось Oy , перпендикулярную рельсам, уравнение движения примет вид

O x : М a=F_торм+F_сопр + Mg sina, (4.15)

O y: 0 = – M g cosa + N. (4.16)

Обозначим sin α = i. Примем cos a = 1. Силу сопротивления движению определим по закону Кулона F_сопр = μ_сопрN = μ_сопрМ g (согласно 4.16). Подставив силу сопротивления в уравнение (4.15), получим для ускорения формулу

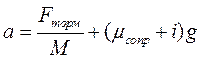. (4.17)

Примем значение силы торможения равным предельному (4.9) значению, F_{торм пред} = μ_сц М g. При таком торможении ускорение будет иметь наибольшее значение. Подставив формулу силы торможения, получим

a_max = g (m_сц +m_сопр +i). (4.18)

Таким образом, при торможении всеми колесами ускорение поезда и тормозной путь 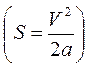от массы поезда не зависят. Сумма коэффициентов в скобках формулы (4.18) имеет значение в интервале 0,25–0,35, и ускорение при торможении в условиях полного сцепления колес с рельсами получается довольно большим, в пределах 2,5–3,5 м/с². При таком экстренном торможении грузы будут сорваны со своих мест, пассажиры упадут. Следует производить служебное торможение в условиях неполного сцепления колес с рельсами.

В случае необходимости торможения поезда с небольшим значением ускорения, достаточно остановить поезд силами торможения только локомотива.При рекуперативном и реостатном торможении ведущие колеса локомотива, продолжая вращаться под действием силы сцепления с рельсами, приводят во вращение якоря тяговых двигателей, которые начинают работать в режиме генераторов. Возникающий момент электромагнитных сил тормозит вращение якоря двигателя и, значит, колеса. Это выгодно. Колесо, не зажатое тормозными колодками, не истирает рельс при поперечном смещении вагона. Вырабатываемая электроэнергия, производимая за счет уменьшения энергии поезда, может отдаваться в контактную сеть.

Предельная сила торможения локомотива, по закону трения, равна F_{торм, пред} = μ_сц mg, где mg – сила тяжести локомотива, μ_сц – коэффициент сцепленияколес с рельсами. Кроме того, на поезд действует сила сопротивления и скатывающая сила. В этом случае уравнение второго закона Ньютона (4.15) для торможения поезда примет вид

O х: М a_max = μ_сц mg + (μ_сопр +i) M g. (4.19)

Откуда максимальное значение ускорения поезда при торможении только локомотивом будет равно

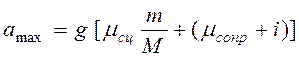. (4.20)

Если принять обычные значения коэффициента сцепления μ_сц= 0,25 и коэффициента (μ_сопр+i)= 0,005, то при массе поезда, в 25 раз больше массы локомотива, получим значение ускорения, вполне приемлемое для грузов и пассажиров, около 0,15 м/с .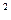

Задачи

1. Сила тяги локомотива со временем возрастает по закону F = 0,5·10⁵ t, Н. Составить уравнение зависимости пути поезда массой 2·10⁶ кг от времени, если коэффициент сопротивления 0,003. В какой момент времени начнется буксование, если коэффициент сцепления колес с рельсами 0,30.

2. Определите предельное ускорение поезда массой 5^.10⁶ кг при трогании с места локомотивом массой 0,3^.10⁶ кг на подъеме с уклоном 0,002. Коэффициент сопротивления 0,002, коэффициент сцепления колес с рельсом 0,25.

3.Определить тормозной путь и время торможения поезда на спуске с уклоном 2 м на 1000 м пути при начальной скорости 20 м/с. Коэффициент сцепления 0,15, коэффициент сопротивления 0,005.

4.Определить, с каким ускорением будет скатываться состав на спуске с уклоном дороги 0,01, если коэффициент сопротивления качению 0,005. Какова будет скорость и время движения состава в конце спуска длиной 10 км.

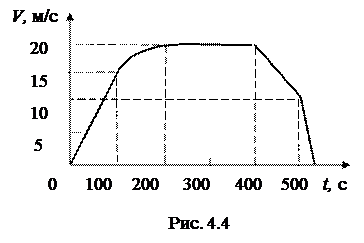5.Определить по графику зависимости скорости от времени движения V(t) поезда массой 3,6·10⁶ кг на подъеме с уклоном 0,002 силу тяги в режиме разгона и при движении с постоянной скоростью, если коэффициент сопротивления 0,005 (рис.4.4).

6. Определить по графику зависимости скорости от времени движения V(t) поезда массой 3,6·10⁶ кг на подъеме с уклоном 0,002 силу сопротивления и коэффициент сопротивления в режиме выбега. Определить силу тяги локомотива при равномерном движении (рис.4.4).

7. Определить предельную массу поезда с локомотивом массой 200 т в двух случаях. При трогании на горизонтальном участке с ускорением 0,1 м/с² и коэффициенте сопротивления 0,008. При движении с постоянной скоростью на подъеме с уклоном 0,01 и коэффициенте сопротивления 0,005. Коэффициент сцепления колес с рельсами 0,25.

5. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА

Движение вагона в составе поезда можно рассматривать относительно инерциальной системы отсчета «Земля». Но задача про вагон решается проще в системе отсчета «Поезд», которую при движении поезда с ускорением следует рассматривать как неинерциальную систему отсчета.

Неинерциальными системами отсчета являются системы отсчета, которые движутся с ускорением относительно инерциальных систем отсчета. В неинерциальных системах отсчета не выполняются законы Ньютона, так как даже без внешнего воздействия тела движутся с ускорением. Однако, если к реальным силам добавить так называемые силы инерции, то применение законов Ньютона в неинерциальных системах отсчета становится возможным.

Силы инерции

Пусть неинерциальная система отсчета движется относительно некоторой инерциальной системы отсчета с ускорением 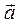. Пусть некоторое тело движется с ускорением 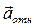относительно неинерциальной системы отсчета. Тогда относительно инерциальной системы отсчета тело движется с ускорением 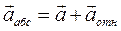. В инерциальной системе отсчета уравнение второго закона Ньютона имеет вид 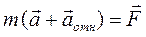. Перепишем его для ускорения относительно неинерциальной системы отсчета

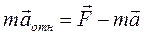. (5.1)

Как видно, второй закон Ньютона применять в неинерциальных системах отсчета можно, если к реальным силам добавить некоторую фиктивную силу, равную произведению массы тела на ускорение неинерциальной системы отсчета и направленной противоположно ускорению:

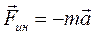. (5.2)

Эти силы называют силами инерции. Силы действуют только в неинерциальных системах отсчета, их можно измерить, но невозможно указать тело, которое является источником сил инерции. Силы инерции фиктивны, они обусловлены не взаимодействием тел, а свойствами самих неинерциальных систем отсчета. Силы инерции действуют на каждую частицу тела, поэтому равнодействующая силы инерции приложена к центру масс тела (как и сила тяжести).

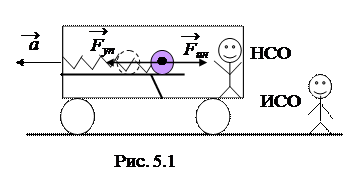Рассмотрим три вида сил инерции. Например, в поезде, который движется с ускорением прямолинейно, на горизонтальном столике лежит шарик на пружинке (рис. 5.1). Пассажир в системе отсчета «Поезд» наблюдает, как шарик растягивает пружинку в направлении против ускорения. То есть для наблюдателя НСО на шарик действует некоторая сила F_ин, но тела, являющего источником силы, не обнаруживает. Эта сила для пассажира вполне реальна, так как противодействует силе упругости пружины, 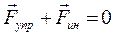. Для инерциального наблюдателя на перроне сил инерции нет, поведение шарика подчиняется второму закону Ньютона: под действием пружины шарик движется с ускорением, как и весь поезд, 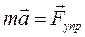. Сопоставляя уравнения, получим, что сила инерции равна произведению массы тела на ускорение неинерциальной системы отсчета и направлена против вектора ускорения: 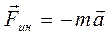. Это тангенциальная или переносная сила инерции.

Аналогично, при движении поезда на повороте, шарик растягивает пружинку по радиусу траектории наружу под действием силы инерции, которую называют центробежной силой. Центробежная сила действует во вращающихся системах отсчета. Она равна произведению массы тела на центростремительное ускорение неинерциальной системы отсчета:

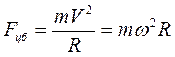. (5.3)

Здесь R – радиус траектории, ω – угловая скорость вращения, V– линейная скорость.

Земля вследствие вращения является неинерциальной системой отсчета. На тела действует центробежная сила инерции, направленная перпендикулярно оси вращения Земли наружу. Однако центростремительное ускорение по сравнению с ускорением свободного падения невелико и поэтому Землю в первом приближении можно считать инерциальной системой отсчета.

Действие центробежной силы широко используется в технике: в центробежных насосах, сепараторах, регуляторах скорости вращения. Центробежная сила действует на несбалансированные вращающиеся детали машин, вызывая вибрацию или даже их разрушение.

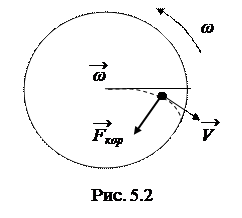Во вращающихся системах отсчета кроме центробежной силы на тела, движущиеся не параллельно оси вращения, действует еще так называемая сила Кориолиса. Например, если катнуть шарик от центра вращающегося диска, то его след на диске оказывается не прямой радиальной линией, а искривлен. Хотя относительно Земли он движется по прямой линии, но участки диска подкатываются под шарик. С точки зрения неинерциального наблюдателя, расположенного на диске, на шарик действует сила, перпендикулярная вектору скорости V относительного движения. Её величина определяется формулой

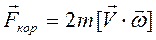. (5.4)

Здесь ω – угловая скорость вращения, V – скорость тела относительно вращающейся системы отсчета.

Тела, движущиеся по Земле, испытывают действие силы Кориолиса. В Северном полушарии эта сила направлена вправо по ходу движения. Сила Кориолиса сравнительно с силой тяжести невелика, однако вызывает боковое смещение траектории снарядов, смещение к востоку падающих с большой высоты тел. Плоскость колебаний шара на длинном подвесе (маятник Фуко) поворачивается под действием силы Кориолиса относительно Земли на 360^о за сутки, но остается постоянной относительно звезд. Действуя на потоки воздуха в атмосфере, она является причиной образования циклонов, пассатов, тайфунов. Действуя на потоки воды, она приводит к повороту морских течений, к подмыванию правого берега рек в Северном полушарии Земли.