Постановка задачи линейного программирования

Методические указания к проведению лекционного занятия

Тема № 9.1. Линейное программирование

План:

1. Основные понятия и определения.

2. Постановка задачи линейного программирования.

3. Примеры построения математических моделей типовых задач линейного программирования.

4. Графический метод решения ЗЛП.

Основные понятия и определения

При решении каких-либо экономических задач часто используют модели математического программирования.

Математическое программирование – это раздел математики, посвящённый решению задач, связанных с нахождением экстремумов функций нескольких переменных при наличии ограничений на переменные.

Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразовании, транспортные задачи и т.п.

Математическое программирование включает в себя линейное, нелинейное, целочисленное, динамическое, стохастическое программирование, теорию игр, теорию массового обслуживания и др.

Базовыми (основными) понятиями математического программирования являются понятия: переменные величины, система ограничений, целевая функция. В описании именно этих понятий заключается этап построения математической модели. Они являются исходными данными для математической модели.

Опр.: Переменными задачи называются величины 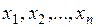, которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора Х = ( ).

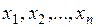Опр.: Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий.

Опр.: Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.

В общем виде задача математического программирования формулируется следующим образом.

Найти экстремум целевой функции

F (Х ) = F ( 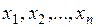) → max (min) (1)

и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений

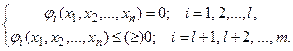(2)

Выбор метода решения задачи математического программирования зависит от исходных данных, т.е. от переменных 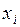, функций F и 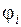. Эти величины определяют и классификацию задач математического программирования.

Исходные данные могут быть детерминированными и случайными.

Опр.: Детерминированными называют такие исходные данные, для которых при составлении модели известны их точные значения.

Если исходные данные принимают в зависимости от случая те или иные значения с определёнными вероятностями, то их называют случайными.

Искомые переменные 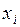могут быть непрерывными и дискретными.

Опр.: Непрерывными называют такие величины, которые в заданном промежутке принимают любые значения.

Опр.: Дискретными называют величины, принимающие заданные значения и эти значения можно пересчитать.

Дискретные переменные, которые могут принимать только целые значения, называют целочисленными.

Зависимости между переменными (целевые функции, ограничения) могут быть линейными и нелинейными.

Опр.: Линейными называют зависимости, в которые все переменные входят в первой степени и с ними выполняются только действия сложения или умножения на число. Если же переменные входят не в первой степени или с ними выполняются другие действия, то зависимости называют нелинейными.

Опр.:Если целевая функция (1) и система ограничений (2) линейны, то задача математического программирования называется задачей линейного программирования (ЗЛП).

Если хотя бы одна из функций F и 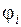нелинейна, то задача математического программирования называется задачей нелинейного программирования.

Если в задаче линейного программирования переменные 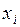- целочисленные, то задача называется задачей целочисленного программирования.

Если хотя бы одна из величин 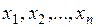не может быть задана детерминировано, т.е. является случайной, то задача математического программирования называется задачей стохастического программирования.

Если величины 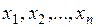принимают только конечное число значений, то задача математического программирования называется задачей дискретного программирования.

Задачи, в которых всякое допустимое решение конструируется в результате некоторого многошагового процесса, называют задачами динамического программирования.

Постановка задачи линейного программирования

Задачу математического программирования (1) – (2) для случая линейного программирования можно представить в виде:

F(Х) = 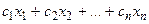→ max (min),

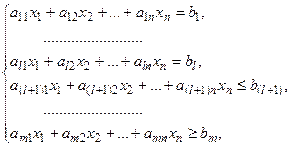
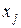≥ 0, j = 1, 2, …, n.

Данную запись называют общей ЗЛП и она означает следующее: необходимо найти экстремум (максимум или минимум) целевой функции F(Х) и соответствующие ему переменные 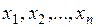, удовлетворяющие заданной системе ограничений и условиям неотрицательности.

В системе ограничений вместо знаков равенства возможны любые знаки неравенств: <, ≤, >, ≥.

Если система ограничений состоит только из неравенств, то ЗЛП называют стандартной.

В том случае, когда все ограничения являются уравнениями, ЗЛП называют канонической.

В координатной форме каноническая ЗЛП имеет вид:

F(Х) = 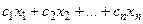→ max (min), (3)

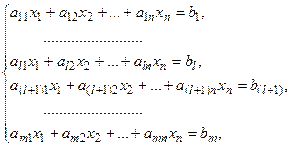(4)

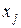≥ 0, j = 1, 2, …, n. (5)

Используя знак суммирования, данную задачу можно записать в компактном виде:

F(Х) = 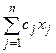→ max (min),

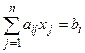, i = 1, 2, …, m, 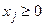, j = 1, 2, …, n.

В матричной форме каноническая ЗЛП имеет вид:

F(Х) = СХ → max (min), АХ = В, ,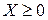

где А – матрица коэффициентов при неизвестных системы уравнений (4), Х – матрица-столбец неизвестных ЗЛП, В – матрица-столбец свободных коэффициентов системы уравнений (4).

Опр.: Допустимым планом (допустимым решением) ЗЛП называется любой n–мерный вектор Х = ( 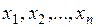), удовлетворяющий системе ограничений и условиям неотрицательности.

Опр.:Множество допустимых решений (планов) ЗЛП образуют область допустимых решений (ОДР).

Опр.: Оптимальным планом (оптимальным решением) ЗЛП называется такой допустимый план задачи, при котором целевая функция достигает экстремума.

Совокупность целевой функции (3), системы ограничений (4) и условий неотрицательности (5) называется математической моделью задачи линейного программирования.