Стоячие волны в линии без потерь

Линия без потерь описывается системой уравнений

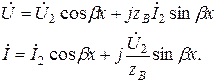
Между длиной волны и коэффициентом фазы существует соотношение

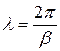отсюда .

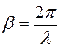Подставляя выражение для коэффициента фазы в систему уравнений, получим

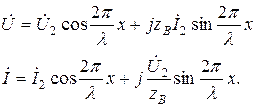
Мы знаем, что напряжение и ток в любой точке линии х можно найти как сумму падающей и отраженной волн.

Точкам, расположенным на расстоянии 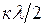от конца линии, соответствуют максимальные значения напряжения, так как фазы падающей и отраженной волн в этих точках совпадают.

На расстояниях, кратных четверти волны 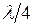от этих точек, падающая и отраженная волны находятся в противофазе и напряжение имеет минимальное значение.

Координаты максимумов и минимумов напряжения не зависят от времени и остаются на одном и том же месте.

Аналогичные рассуждения можно провести и для тока, только положения максимумов и минимумов тока смещены относительно максимумов и минимумов напряжения на четверть длины волны.

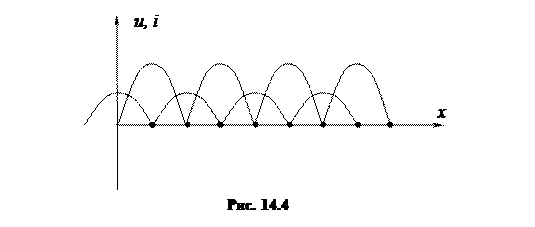В том случае, если коэффициент отражения равен единице |p| = 1, то есть при равенстве амплитуд отраженной и падающей волн в линии возникают стоячие волны напряжения и тока. Кривые действующих значений в этом случае представляют собой выпрямленные синусоиды (рис. 14.4).

На линии образуются узлы, то есть точки, в которых напряжение и ток равны нулю, и пучности – точки, в которых ток и напряжение максимальны. Причем узлам напряжения соответствуют пучности тока, и, наоборот, узлам тока соответствуют пучности напряжения.

Условие возникновения стоячих волн может выполняться в трех случаях:

1) при холостом ходе, когда Z_н = ∞;

2) при коротком замыкании, когда Z_н = 0;

3) при чисто реактивной нагрузке, когда Z_н = ±jХ.

Рассмотрим подробнее эти случаи.

Холостой ход

При холостом ходе ток нагрузки равен нулю и уравнения линии примут следующий вид:

;

.

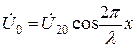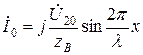В точках, где 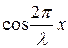=0 будут находиться узлы напряжения.

Решением этого уравнения является .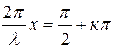

Отсюда следует, что узлы будут находиться в точках, координаты которых удовлетворяют условию

,

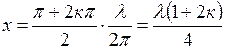то есть в точках с координатами

.

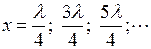Пучности напряжения расположены в точках, где 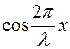= ±1, то есть на расстояниях 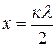, или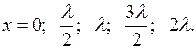

Так как ток изменяется по закону синусов, то для него справедливы обратные расположения узлов и пучностей. В этом случае в конце линии будет пучность напряжения и узел тока (рис. 14.5).

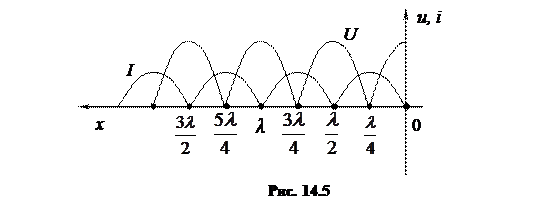Входное сопротивление линии в этом случае определится как

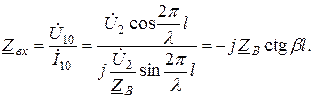
Таким образом, для линий разной длины входное сопротивление может иметь различный характер:

при 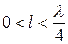имеет емкостный характер;

при 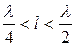– индуктивный характер;

при 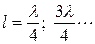входное сопротивление равно нулю, что соответствует режиму резонанса напряжений;

при 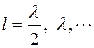входное сопротивление равно ∞, что соответствует режиму резонанса токов.

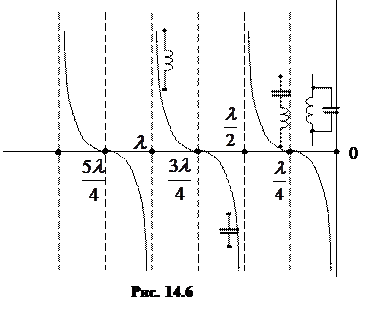Изменение входного сопротивления вдоль линии проиллюстрировано на рис. 14.6.

Короткое замыкание

При коротком замыкании напряжение на нагрузке равно нулю, и уравнения линии принимают следующий вид:

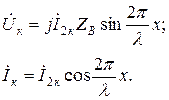
Тогда в конце линии, то есть при х = 0, и в точках, удаленных от конца линии на целое число полуволн 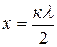, будут узлы напряжения и пучности тока. В точках с координатами 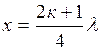будут пучности напряжения и узлы тока (рис. 14.7).

Входное сопротивление линии

.

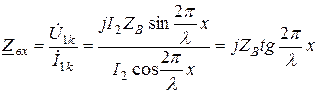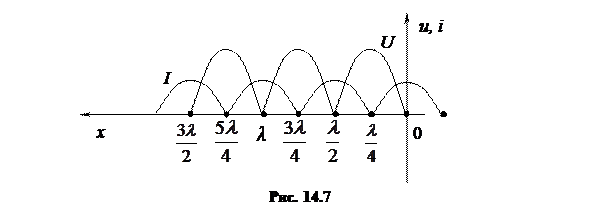Таким образом, входное сопротивление

при 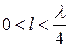имеет индуктивный характер;

при 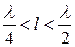– емкостный характер;

при 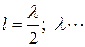входное сопротивление равно нулю, что соответствует режиму резонанса напряжений;

при 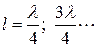входное сопротивление равно ∞, что соответствует режиму резонанса токов.

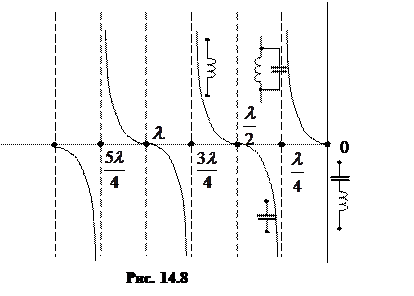Изменение входного сопротивления вдоль линии проиллюстрировано на рис. 14.8.

Реактивная нагрузка

В случае реактивной нагрузки 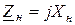, и уравнения для тока и напряжения примут следующий вид

;

.

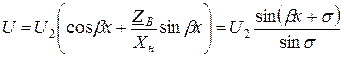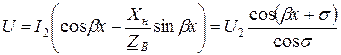В этом случае также получаем стоячие волны, но, так как имеется начальная фаза, в конце линии не будет ни узла, ни пучности.

Так как в любой момент времени в узлах тока I = 0, а в узлах напряжения U = 0, то в этих точках линии мощность равна нулю. В остальных точках мощность реактивная, так как ток и напряжение находятся в противофазе. В этом случае энергия не передается вдоль линии, а происходит обмен энергией электрического и магнитного полей.

Энергия, передаваемая вдоль линии, складывается из энергии электрического и магнитного полей. В том случае, когда к концу линии без потерь подключено сопротивление, равное волновому, вся энергия, доставляемая падающей волной, поглощается в сопротивлении нагрузки.

Если линия разомкнута, падающая волна встречает бесконечно большое сопротивление, ток в конце линии обращается в нуль и энергия магнитного поля переходит в энергию электрического поля.

Если линия замкнута накоротко, падающая волна встречает сопротивление, равное нулю, напряжение в конце линии обращается в нуль, энергия электрического поля переходит в энергию магнитного.

Если линия разомкнута, падающая волна встречает бесконечно большое сопротивление.