Датчики скорости, расхода и уровня жидкости
5.10.1. Элементарные понятия
Движущаяся жидкость - это течение. На практике описание течения требует измерения скорости, плотности, давления и температуры в различных точках потока.
В некотором диапазоне условий физические параметры течения в данной точке могут быть постоянными или изменяться во времени.
В первом случае течение называется ламинарным, во втором - турбулентным.
Для облегчения описания и сравнения различных течений в механике жидкости обычно т пользуются безразмерными критериями, позволяющими уменьшить число параметров, которыми определяется рассматриваемое течение.
В случае изотермического течения несжимаемой жидкости (плотность ρ и температура T постоянны) единственным безразмерным параметром, достаточным для определения этого течения, является число Рейнольдса 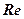
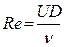 , (5.96)
, (5.96)
где 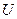 - характерная скорость течения (например, средняя скорость в трубе, определяемая выражением
- характерная скорость течения (например, средняя скорость в трубе, определяемая выражением 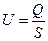 , в котором
, в котором 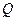 - объемный расход,
- объемный расход, 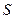 - площадь поперечного сечения трубы);
- площадь поперечного сечения трубы);
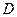 - характерная длина (например, диаметр трубы);
- характерная длина (например, диаметр трубы);
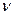 - кинематическая вязкость жидкости, т.е. отношение динамической вязкости жидкости
- кинематическая вязкость жидкости, т.е. отношение динамической вязкости жидкости 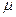 к ее плотности
к ее плотности 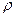 .
.
В аналогичных геометрических условиях два изотермических течения несжимаемой жидкости подобны, если их числа Рейнольдса одинаковы.
Пример. Имеется два течения в трубах диаметром 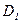 и
и 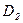 .
.
Пусть 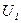 и
и 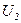 - средние скорости течения в них, а
- средние скорости течения в них, а 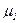 и
и 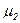 - соответствующие вязкости.
- соответствующие вязкости.
Пусть выполняется условие
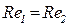 , т.е.
, т.е. 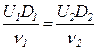 . (5.97)
. (5.97)
Соотношение (5.96) справедливо и для произвольного значения характерной длины 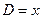 , т.е.
, т.е.
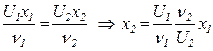 . (5.98)
. (5.98)
Согласно (5.97) имеем 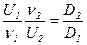 .
.
Тогда последнее выражение из (5.98) может быть представлено в виде
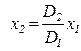 . (5.99)
. (5.99)
Из рассмотрения (5.98) и (5.99) вытекает вывод, что, зная местную скорость 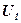 на расстоянии
на расстоянии 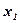 от стенки в первой трубе диаметром
от стенки в первой трубе диаметром 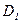 , можно определить скорость течения
, можно определить скорость течения 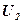 во второй трубе диаметром
во второй трубе диаметром 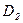 на расстоянии
на расстоянии 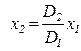 от ее стенки.
от ее стенки.
Для течения газа с большой скоростью можно записать
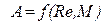 ,
,
где 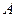 - некоторая величина, описывающая газ,
- некоторая величина, описывающая газ,
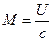 - число Маха,
- число Маха, 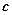 - скорость звука.
- скорость звука.
Таким образом, число безразмерных критериев в этом случае увеличилось до двух.
5.10.1.1. Уравнения механики жидкости в общем случае
Уравнение неразрывности (уравнение сохранения массы)
Имеет вид
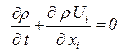 , (5.100)
, (5.100)
где 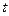 - время;
- время;
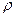 - плотность жидкости;
- плотность жидкости;
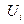 - компонента вектора скорости (ее проекция на оси в трехмерном пространстве
- компонента вектора скорости (ее проекция на оси в трехмерном пространстве 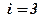 );
);
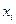 - координата пространства.
- координата пространства.
Уравнение сохранения количества движения
Уравнение сохранения количества движения жидкости, находящейся в поле Ньютоновской силы тяготения, в общем виде записывается как
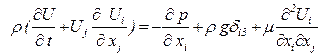 , (5.101)
, (5.101)
где 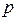 -давление;
-давление;
g – ускорение свободного падения;
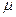 - динамическая вязкость;
- динамическая вязкость;
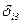 - коэффициент, учитывающий составляющую веса, причем
- коэффициент, учитывающий составляющую веса, причем 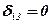 при
при 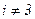 и
и 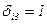 при
при 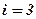 ось “3” вертикальна.
ось “3” вертикальна.
Уравнение сохранения энергии
Уравнение имеет вид
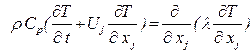 , (5.102)
, (5.102)
где 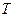 - температура;
- температура;
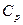 – удельная теплоемкость при постоянном давлении;
– удельная теплоемкость при постоянном давлении;
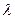 - коэффициент теплопроводности.
- коэффициент теплопроводности.
Уравнение состояния
Для полного описания движения необходимо принять во внимание уравнение состояния. Например, уравнение состояния совершенного газа имеет вид
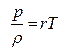 , (5.103)
, (5.103)
где 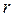 - газовая постоянная.
- газовая постоянная.
Искомыми величинами в выражениях (5.100) - (5.103) являются компоненты скорости 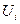 , плотность
, плотность 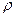 , давление
, давление 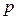 и температура
и температура 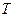 .
.
5.10.1.2. Одномерное течение
В технических задачах часто достаточно одномерное описание течений, в которое входят более общие параметры.
Схема одномерного течения представлена на рисунке 5.26.
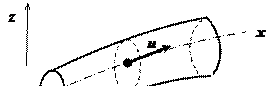 При этом для течения, ограниченного твердыми стенками, в котором скорость считается равномерной, в каждом поперечном сечении уравнение неразрывности (5.100) превращается в уравнение сохранения массового расхода
При этом для течения, ограниченного твердыми стенками, в котором скорость считается равномерной, в каждом поперечном сечении уравнение неразрывности (5.100) превращается в уравнение сохранения массового расхода 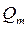 :
:
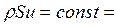
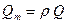 (5.104)
(5.104)
где 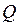 - объемный расход.
- объемный расход.
Точно так же из уравнения охранения количества движения (5.101), записанного для одной и той же линии тока, в случае течения несжимаемой ( 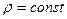 ) и невязкой (
) и невязкой ( 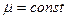 ) жидкости получаем:
) жидкости получаем:
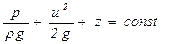 . (5.105)
. (5.105)
Это – уравнение Бернулли, которое выражает закон сохранения суммы величин, называемой напором.
Влияние вязкости учитывают, вводя поправку 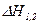 для течения между сечениями 1 и 2:
для течения между сечениями 1 и 2:
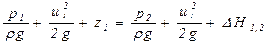 . (5.106)
. (5.106)
Аэро- и гидродинамические силы
Определение сил, с которым жидкость действует на твердые тела, - одна из важных задач проектирования.
К таким силам можно отнести, например:
- силу ветра;
 - сопротивление жидкости, действующее на суда;
- сопротивление жидкости, действующее на суда;
- подъемная сила, лобовое сопротивление, действующие на летательные аппараты и их элементы конструкции и др.
Когда жидкость (газ) обтекает твердое тело, (или то же самое, когда тело перемещается в жидкости (в газе)), оно подвергается воздействию системы сил, которую характеризуют как результирующие сила и момент (в общем случае 6 составляющих). На рисунке 5.27: F – результирующая сила; Q – проекция силы, параллельной скорости V (лобовое сопротивление); P – подъемная сила, перпендикулярная вектору скорости; S - площадь миделевого (поперечного) сечения.
При этом силы определяются по зависимостям:
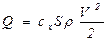 ,
, 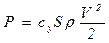 ,
,
где 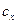 ,
, 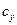 - коэффициенты подъемной силы и лобового сопротивления соответственно;
- коэффициенты подъемной силы и лобового сопротивления соответственно;
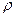 - плотность жидкости (газа).
- плотность жидкости (газа).
5.10.2 Датчики и методы измерения скорости жидкости
5.10.2.1. Общие определения
Скорость обычно измеряют косвенно, определяя воздействие, которое она оказывает:
- на физические характеристики чувствительности элемента;
- на определенные физические явления, объектом которых является чувствительный элемент.
Чувствительным элементом может быть как сама жидкость, так и один из элементов датчика.
Если чувствительным элементом является сама жидкость, то ее скорость определяет:
- динамическое давление 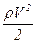 ;
;
- доплеровский эффект, которому подвергается лазерное или ультразвуковое излучение;
- время пробега радиоактивного изотопа между заданными сечениями.
Таким образом, определить скорость можно с помощью датчика, для измерения какого-либо физического параметра: давления, светового потока, ультразвукового и лазерного излучения.
Если чувствительный элемент является элементом датчика, помещенного в жидкость, то показателем ее скорости может служить какая-либо ее физическая характеристика, например:
- температура и, следовательно, сопротивление нагретой нити, питаемой постоянным током;
- скорость вращения помещенной в поток крыльчатки.
5.10.2.2. Термоанемометры с нагретой металлической нитью или лентой
Если поместить в поток металлическую нить или ленту, температура которой T поддерживается с помощью эффекта Джоуля постоянной и превышающей температуру потока, то между ней и потоком возникает конвективный теплообмен.
Этот теплообмен зависит от:
- физических свойств жидкости;
- разности температур нагретого элемента и жидкости.
Равновесная температура T нити или ленты, являющейся чувствительным элементом датчика, определяется путем измерения ее электрического сопротивления, которое зависит от выделенной джоулевой теплоты и скорости жидкости, которую необходимо определить.
Выведем требуемые соотношения.
Количество джоулевой теплоты можно определить по выражению
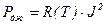 , (5.107)
, (5.107)
где 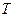 - температура чувствительного элемента (нити, ленты);
- температура чувствительного элемента (нити, ленты);
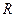 - резистор (активное сопротивление);
- резистор (активное сопротивление);
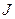 - сила постоянного тока.
- сила постоянного тока.
Полагая, что теплообмен осуществляется только конвекцией в жидкости, имеющей температуру 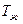 , количество теплоты, участвующего в теплообмене, можно записать:
, количество теплоты, участвующего в теплообмене, можно записать:
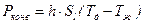 , (5.108)
, (5.108)
где 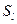 - боковая поверхность чувствительного элемента (для нити -
- боковая поверхность чувствительного элемента (для нити - 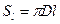 ,
, 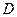 - диаметр сечения нити;
- диаметр сечения нити; 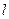 - ее длина; для ленты
- ее длина; для ленты 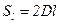 ,
, 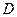 - ее ширина и
- ее ширина и 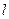 - длина);
- длина);
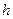 - коэффициент теплообмена;
- коэффициент теплообмена;
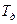 - температура датчика.
- температура датчика.
При тепловом равновесии имеет место
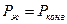 .
.
Тогда из (5.107) и (5.108) следует
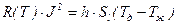 . (5.109)
. (5.109)
Скорость жидкости V входит в выражение для 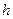 , для которого предложены различные эмпирические формулы в зависимости от характеристики течения.
, для которого предложены различные эмпирические формулы в зависимости от характеристики течения.
Существует формула Кинга
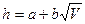 , 5.110)
, 5.110)
где 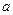 и
и 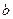 - постоянные для конкретной жидкости и датчика.
- постоянные для конкретной жидкости и датчика.
Тогда из (5.109) имеем
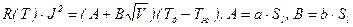 . (5.111)
. (5.111)
 |
Из последней зависимости может быть легко получено выражение для искомой скорости потока жидкости.
 Из сказанного выше вытекает принципиального схема определения скорости, которая может быть представлена в виде, приведенном на рисунке 5.28.
Из сказанного выше вытекает принципиального схема определения скорости, которая может быть представлена в виде, приведенном на рисунке 5.28.
5.10.2.3. Чашечные и крыльчатые анемометры
Анемометры этого типа, называемые также “вертушками”, снабжены чувствительными элементами в виде системы чашек или крыльчаток, приводимых во вращение движущейся жидкостью.
Скорость вращения, измеряемая соответствующим тахометрическим устройством, пропорциональна скорости течения жидкости.
На рисунке 5.29 приведена схема чашечного анемометра.
Выведем уравнения равновесия анемометра.
Линейная скорость чашек 1 и 3 равна соответственно uи – uи направлены они параллельно скорости потока V.
Поэтому силы лобового сопротивления определяются как:
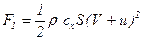 ; (5.112)
; (5.112)
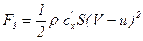 , (5.113)
, (5.113)
где 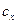 ,
, 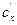 - коэффициенты лобового сопротивления каждой из сторон полусферических чашек;
- коэффициенты лобового сопротивления каждой из сторон полусферических чашек;
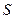 - площадь миделевого сечения чашек;
- площадь миделевого сечения чашек;
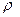 - плотность жидкости.
- плотность жидкости.
Очевидно, что в установившемся движении имеет место 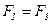 .
.
Тогда их двух предыдущих выражений имеем:
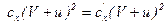
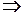
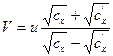 . (5.114)
. (5.114)
Численные значения коэффициентов для полой полусферы равны 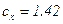 и
и 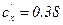 . Отсюда получаем компактное выражение
. Отсюда получаем компактное выражение
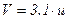 , (5.115)
, (5.115)
в котором значение скорости u легко можно получить, имея информацию об угловой скорости вращения системы крыльчаток и расстояние до чашек от оси вращения системы.
5.10.2.4. Методы измерения скорости косвенными датчиками
Скорость жидкости можно определить косвенно, по воздействию, оказываемому на некоторую зависящую от скорости физическую величину, измеряемую рассматриваемыми датчиками.
 Измерение трубкой Пито
Измерение трубкой Пито
Уравнение Бернулли:
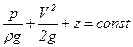
позволяет связать скорость V с давлением p1, p2 соответственно в точках 1 и 2 (рисунок 5.30).
Для такого случая получаем:
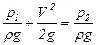
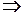
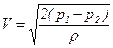 . (5.116)
. (5.116)
Как следует из рассмотрения полученного выражения, для определения скорости потока необходимо знать значения давления на срезе трубки (в точке 1) и на ее стенке (в точке 2).
Ультразвуковой анемометр
Схема такого анемометра предсталена на рисунке 5.31.
Cистема измерения состоит из излучателя ультразвуковых импульсов и приемника, находящегося на расстоянии L от излучателя.
На рисунке:
V – скорость движения потока;
α – угол между вектором скорости и направлением распространения волн.
Длительность распространения импульсов между излучателем и приемником равна
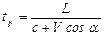 . (5.117)
. (5.117)
Отсюда
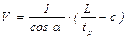 . (5.118)
. (5.118)
Как следует из (5.118), скорость потока определяется достаточно просто.
5.10.3. Измерение расхода жидкости
Измерение расхода имеет большое значение в трубопроводных транспортных системах (газо- и нефтепроводы), в промышленных установках.
5.10.3.1. Электромагнитные расходомеры
 Принцип действия
Принцип действия
Схема работы расходомера поясняется рисунком 5.32.
Рассмотрим перемещение за время dt отрезка проводника M1M2 = l в магнитном поле с индуктивностью B со скоростью V. При этом угол между проводником и вектором скорости равен θ.
Из рассмотрения рисунка можно получить следующие соотношения:
- для ометаемой проводником элементарной площади
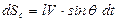
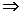
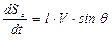 ; (5.119)
; (5.119)
- для магнитного потока
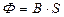 ; (5.120)
; (5.120)
- для индуциированной э.д.с. (закон Ленца)
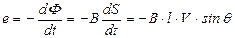 . (5.121)
. (5.121)
Если все три вектора перпендикулярны, то (5.121) дает
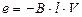 . (5.122)
. (5.122)
Полученная формула может быть распространена и на случай течения жидкости в трубопроводе диаметром D со скоростью V, перпендикулярной B
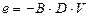 , (5.122)
, (5.122)
т.е. величина э.д.с. 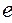 пропорциональна скорости V,а соответственно и расходу
пропорциональна скорости V,а соответственно и расходу 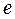 ~
~ 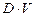 .
.
Реализация метода
Схема, показывающая, как может быть реализован метод, приведена на рисунке 5.33.

Магнитная индукция создается двумя катушками, расположенными диаметрально противоположно по обе стороны трубопровода, расход в котором измеряется.
Здесь используется трубопровод из немагнитного материала.
Два электрода, воспринимающие сигнал, располагаются на концах диаметра поперечного сечения, перпендикулярного силовым линиям магнитного поля.
Достоинства магнитных расходомеров
К ним можно отнести:
- измерение не зависит от различных свойств жидкости;
- измерение практически не зависит от распределения скорости в трубопроводе;
- в зоне измерений не происходит потери напора, т.к. сечение трубопровода не загромождается ничем;
- у расходомера отсутствуют подвижные изнашиваемые элементы;
- коррозионная стойкость (что особенно важно, например, в случае измерения расхода кислот).
5.10.3.2. Механические расходомеры с электрическим преобразователем
На чувствительный элемент, помещенный в трубопровод, воздействуют аэро- или гидродинамические силы движущейся массы, которые вызывают его вращение (например, под действием ротора турбины) или перемещение (под действием лопастей).
Соответствующий датчик (в первом случае – тахометр, во втором – датчик положения) генерирует электрический сигнал, пропорциональный расходу жидкости.
 Турбинный расходомер
Турбинный расходомер
Принцип действия такой же, как у крыльчатых анемометров: приводит во вращение трубку, размещенную на оси трубопровода.
Частота вращения турбины N (число оборотов в единицу времени) пропорциональна расходу Q:
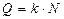 . (5.122)
. (5.122)
 Коэффициент
Коэффициент 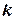 является параметром конструкции расходомера, не зависящим от рода жидкости.
является параметром конструкции расходомера, не зависящим от рода жидкости.
Из теоретического анализа размерности следует, что соотношение 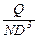 (где
(где 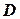 - диаметр трубопровода) зависит от числа Рейнольдса
- диаметр трубопровода) зависит от числа Рейнольдса 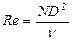 .
.
Для больших чисел 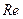 соотношение
соотношение 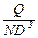 не зависит от
не зависит от 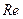 (рисунок 5.34). В этом случае характеристика расходомера является линейной.
(рисунок 5.34). В этом случае характеристика расходомера является линейной.
Достоинством турбинных расходомеров является удобство использования генерируемых ими электрических сигналов.
К недостаткам следует отнести то, что можно использовать такие датчики только там, где отсутствуют возмущения течения жидкости.
Ротаметр
Ротаметр (рисунок 5.35) состоит из небольшого поплавка, помещенного в вертикальной конической трубке. Поплавок находится в равновесии под действием, с одной стороны, архимедовой выталкивающей силы и силы лобового сопротивления и, с другой стороны, силы его веса:
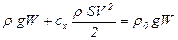 . (5.123)
. (5.123)
Здесь 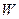 - объем поплавка;
- объем поплавка; 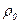 - плотность его материала;
- плотность его материала; 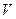 - скорость жидкости;
- скорость жидкости; 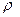 - ее плотность;
- ее плотность; 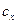 - коэффициент лобового сопротивления;
- коэффициент лобового сопротивления; 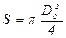 - площадь миделевого сечения поплавка;
- площадь миделевого сечения поплавка; 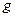 - ускорение свободного падения.
- ускорение свободного падения.
Из (5.123) получим скорость
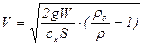 . (5.124)
. (5.124)
Диаметр сечения трубки на уровне, на котором находится поплавок в равновесном состоянии, линейно зависит от этого уровня (высоты) 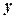 :
:
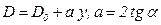 ,
,
где 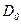 - диаметр поплавка;
- диаметр поплавка;
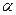 - угол конусности.
- угол конусности.
Расход жидкости можно выразить как
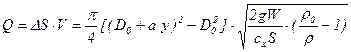 . (5.125)
. (5.125)
Как следует из (5.125), расход пропорционален уровню (высоте) жидкости.
Отсчет положения поплавка производится либо по шкале, нанесенной непосредственно на стеклянную коническую трубку, либо с помощью равномерно расположенных фотоэлементов, либо путем соединения поплавка через стержень с сердечником трансформатора.
Расходомеры с сужающимися устройствами
Сужение трубопровода или изменение его направления вызывает возникновение разности давления 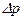 перед сужением (поворотом) и за ним, которая связана с расходом
перед сужением (поворотом) и за ним, которая связана с расходом 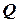 соотношением
соотношением

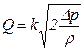 , (5.126)
, (5.126)
где 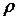 - плотность жидкости;
- плотность жидкости; 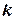 - константа, определяемая в некотором диапазоне чисел Рейнольдса только геометрией устройства.
- константа, определяемая в некотором диапазоне чисел Рейнольдса только геометрией устройства.
Схема одного из возможных таких устройств приведено на рисунке 5.36. В нем измеряемый сигнал перепада давления 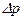 , входящий в выражение (5.126), генерирует дифференциальный датчик перепада давления.
, входящий в выражение (5.126), генерирует дифференциальный датчик перепада давления.
5.10.3.3. Ультразвуковой расходомер
 |
Схемы таких расходомеров представлены на рисунке 5.37.
Принцип действия расходомеров аналогичен ультразвуковому анемометру, в основе работы которого лежит соотношение
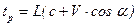 - (5.127)
- (5.127)
время распространения последовательности ультразвуковых волн на расстояние 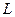 .
.
Время 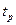 - зависит от скорости звука
- зависит от скорости звука 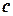 в жидкости, зависящей от свойств жидкости и от ее температуры
в жидкости, зависящей от свойств жидкости и от ее температуры 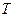 :
: 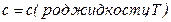 .
.
Можно получить выражение, не зависящее от скорости звука, измеряя эффективное значение величины 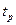 , когда каждый из двух пьезоэлектрических элементов поочередно используется сначала - в качестве излучателя, а затем – в качестве приемника.
, когда каждый из двух пьезоэлектрических элементов поочередно используется сначала - в качестве излучателя, а затем – в качестве приемника.
Справедливы соотношения:
- для направления “1 – 2”
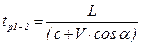 ; (5.128)
; (5.128)
- для направления “2 – 1”
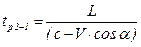 , (5.129)
, (5.129)
из которых получаем

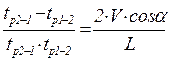 ,
, 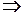
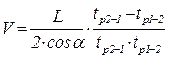 (5.130)
(5.130)
Используя полученную таким образом скорость, легко определить расход жидкости Q.
5.10.3.4. Тепловой измеритель массового расхода
Схема такого измерителя приведена на рисунке 5.38.
Принцип работы заключается в следующем.
Измерительное устройство состоит из тонкостенной металлической трубки малого диаметра, на внешней поверхности которой намотан проволочный нагреватель, а с противоположных сторон от него симметрично установлены два датчика температуры: T1 -выше по потоку, T2 – ниже по потоку.
|
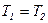 . При наличии расхода, очевидно, что температура
. При наличии расхода, очевидно, что температура 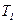 падает, а температура
падает, а температура 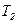 растет.
растет. Разность температур 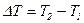 пропорциональна массовому расходу
пропорциональна массовому расходу 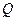 .
.
5.10.3.5. Измеритель массового расхода, использующий силу Кориолиса
 Законами механики установлено, что на массу
Законами механики установлено, что на массу 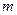 , движущуюся со скоростью
, движущуюся со скоростью 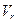 относительно системы отсчета, находящуюся во вращательном движении с угловой скоростью
относительно системы отсчета, находящуюся во вращательном движении с угловой скоростью 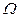 , действует сила
, действует сила 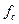 , называемая силой Кориолиса и описываемая формулой
, называемая силой Кориолиса и описываемая формулой
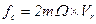 . (5.131)
. (5.131)
Схема измерителя приведена на рисунке 5.39.
Жидкость, массовый расход которой необходимо измерить, течет со скоростью 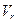 через измерительную трубку U – образной формы.
через измерительную трубку U – образной формы.
Трубка совершает колебательные движения относительно оси 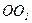 , перпендикулярной рукавам трубки с мгновенной скоростью
, перпендикулярной рукавам трубки с мгновенной скоростью 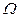 .
.
Здесь справедливы следующие соотношения.
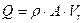 - массовый расход;
- массовый расход;
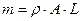 - масса жидкости в одном из рукавов;
- масса жидкости в одном из рукавов;
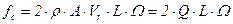 - сила Кориолиса, действующая на один из рукавов;
- сила Кориолиса, действующая на один из рукавов;
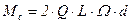 - момент сил Кориолиса на жидкость в обоих рукавах.
- момент сил Кориолиса на жидкость в обоих рукавах.
В приведенных выражениях: 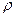 - плотность жидкости;
- плотность жидкости; 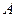 - площадь поперечного сечения U-образной трубки;
- площадь поперечного сечения U-образной трубки; 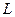 - длина одного из рукавов;
- длина одного из рукавов; 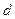 - расстояние между рукавами.
- расстояние между рукавами.
Под действием момента сил Кориолиса 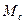 U-образная трубка поворачивается на некоторый угол
U-образная трубка поворачивается на некоторый угол 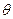 и уравновешивается моментом действующих в противоположном направлении сил упругости
и уравновешивается моментом действующих в противоположном направлении сил упругости
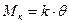 .
.
В положении равновесия имеем
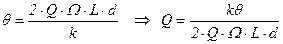 (5.132)
(5.132)
Угловая скорость 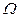 - является функцией времени, как и угол
- является функцией времени, как и угол 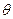 . Значение угла можно измерить датчиками положения, сигналы которых после преобразования позволяют получить напряжение, пропорциональное расходу
. Значение угла можно измерить датчиками положения, сигналы которых после преобразования позволяют получить напряжение, пропорциональное расходу 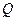 .
.
Достоинства рассмотренного измерителя очевидны. К ним можно отнести следующее:
- показания прибора не зависят от электрофизических свойств жидкости; не надо знать ее плотность, вязкость, давление, температуру;
- особенно подходит данный датчик для неэлектропроводных, заряженных (смеси жидкости с твердыми частицами), двухфазных (эмульсии), неньютоновских (у которых вязкость зависит от скорости) жидкостей.
5.10.4. Измерение и указание уровня жидкости
Получение информации об уровне жидкости может осуществляться двумя способами:
- в виде непрерывного измерения;
- в виде указания предельных величин.
Существует классификация наиболее употребительных методов измерения уровня:
- гидростатические методы с преобразованием в электрический сигнал;
- основанные на электрофизических свойствах жидкости;
- использующие взаимодействие какого-либо излучения жидкости.
5.10.4.1. Гидростатические методы
Сигнал, генерируемый измерительным прибором, является в этом случае функцией высоты уровня жидкости h.
Примеры представлены на рисунке 5.40.
На рисунке  5.40 а) приведен поплавковый датчик. Поплавок на поверхности жидкости жестко связан с помощью тросов и блоков с аналоговым (ленточным потенциометр) или цифровым (градуированный диск) датчиком положения, поставляющим электрический сигнал, соответствующий уровню жидкости.
5.40 а) приведен поплавковый датчик. Поплавок на поверхности жидкости жестко связан с помощью тросов и блоков с аналоговым (ленточным потенциометр) или цифровым (градуированный диск) датчиком положения, поставляющим электрический сигнал, соответствующий уровню жидкости.
Плунжерный датчик выталкивающей силы представлен на рисунке 5.40 б).
Здесь плунжер представляет собой погруженный в жидкость плунжер, высота которого не меньше максимальной высоты жидкости в резервуаре. Плунжер подвешен к динамометрическому датчику, находящемуся под действием силы F, зависящей от гидростатической высоты. Можно привести следующие соотношения, очевидные для данного случая:
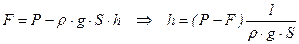 , (5.133)
, (5.133)
где 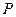 - вес плунжера;
- вес плунжера;
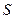 - площадь его поперечного сечения;
- площадь его поперечного сечения;
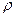 - плотность жидкости;
- плотность жидкости;
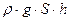 - архимедова выталкивающая сила.
- архимедова выталкивающая сила.
Рисунок 5.20 в) демонстрирует дифференциальный датчик перепада давления. Датчик располагается у дна резервуара, где давление 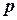 равно
равно
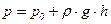 , (5.134)
, (5.134)
где 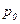 - давление в свободной от жидкости верхней части резервуара;
- давление в свободной от жидкости верхней части резервуара;
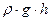 - гидростатическое давление на высоте
- гидростатическое давление на высоте 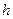 в жидкости.
в жидкости.
Чувствительным элементом датчика является мембрана, с одной стороны которой действует давление 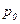 , а с другой -
, а с другой - 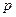 . Деформация мембраны, преобразованная в электрический сигнал, пропорциональна высоте уровня жидкости.
. Деформация мембраны, преобразованная в электрический сигнал, пропорциональна высоте уровня жидкости.
Датчики влажности
5.11.1. Определения
Рассмотрим влажный воздух.
Введем следующие обозначения, связанные с ним:
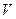 - объем;
- объем;
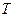 - температура;
- температура;
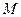 - масса воздуха, при этом
- масса воздуха, при этом
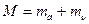 , (5.135)
, (5.135)
где 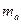
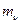 - масса соответственно сухого воздуха и водяного пара;
- масса соответственно сухого воздуха и водяного пара;
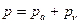 - (5.136)
- (5.136)
давление барометрическое, причем
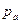 ,
, 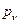 - парциальное давление сухого воздуха и давление водяного пара.
- парциальное давление сухого воздуха и давление водяного пара.
Массовое отношение влажности 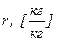
Определяется как
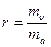 - (5.137)
- (5.137)
отношение массы водяного пара к массе сухого воздуха, в смеси которого находится этот водяной пар.
Эта величина характеризует влажность.
Давление насыщенного пара 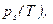
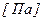
Это максимальное давление, которое может принимать парциальное давление пара 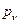 при температуре T.
при температуре T.
Относительная влажность 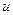 ,
, 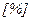
Это отношение парциального давления пара воды при температуре T к давлению насыщенного пара при этой температуре
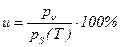 . (5.138)
. (5.138)
Это наиболее часто используемый показатель влажности.
Температура точки росы 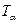 ,
, 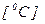
Это температура, до которой необходимо охладить влажный воздух, чтобы достичь насыщения, сохраняя постоянным массовое отношение влаги в процессе охлаждения. При температуре росы имеет место
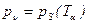 . (5.139)
. (5.139)
Температура влажного термометра 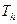 ,
, 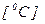
Это температура равновесного испарения воды в воздух в случае, когда необходимая для испарения теплота поступает только из воздуха.
5.11.2. Гигрометры
Гигрометры – это приборы для измерения характеристик влажного воздуха.
Гигрометры можно разделить на две группы:
- гигрометры, основанные на физическом законе, позволяющем непосредственно определить влажность (сорбционные гигрометры);
- гигрометры, принцип действия которых основан на измерении свойств тела, связанных с влажностью (импедансные гигрометры).
Эти гигрометры позволяют определить один из параметров воздуха:
- температуру точки росы 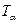 ;
;
- температуру влажного термометра 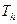 ;
;
- относительную влажность 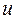 .
.
5.11.2.1. Гигрометры на основе измерения импеданса
Чувствительный элемент состоит из гигроскопического вещества, у которого происходит изменение какого-либо электрического параметра (сопротивление или емкость) при изменении влажности.
 Импеданс гигрометра можно разделить на:
Импеданс гигрометра можно разделить на:
- резистивный;
- емкостной.
Гигрометр резистивного типа
Определенное количество гигроскопического вещества наносится на подложку. К этой же подложке крепятся два металлических электрода.
Сопротивление между электродами зависит от содержания воды, т.е. от влажности.
Общий вид зависимости содержания воды от влажности при температуре T (изотерма сорбции) представлен на рисунке 5.41.
Как видно из рисунка, содержание воды зависит от относительной влажности 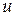 и температуры окружающей среды T.
и температуры окружающей среды T.
Зависимость между относительной влажностью и сопротивлением можно изобразить в виде соответствующей зависимости. На следующем рисунке (рисунок 5.42) представлена типичная кривая зависимости сопротивления 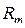 от относительной влажности.
от относительной влажности.
В действительности сопротивление 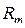 помимо влажности зависит и от температуры T.
помимо влажности зависит и от температуры T.
Влияние температуры можно компенсировать с помощью потенциометрической схемы, представленной на рисунке 5.43.
Здесь сопротивление 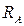 включается последовательно
включается последовательно 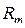 и его зависимость от температуры такая же, как и у резистора
и его зависимость от температуры такая же, как и у резистора 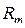 .
.
Емкостной гигрометр на основе полимерного диэлектрика
В таком гигрометре слой полимерного диэлектрика поглощает из воздуха молекулы воды. В результате устанавливается равновесие с воздухом. Это приводит к изменению диэлектрической постоянной слоя и, соответственно, к изменению емкости конденсатора, в котором используется этот диэлектрик.
Акустические датчики
Звуковые волны проявляются, главным образом, через вызываемые ими изменения давления и скорости.
Остановимся на основных понятиях и подходах к рассматриваемому вопросу.
5.12.1. Распространение плоской волны
Для физического описания течения используются законы:
- сохранения массы и количества движения;
- уравнение состояния.
С помощью этих соотношений можно получить, что возмущения малой амплитуды распространяются со скоростью, выражаемой по формуле:
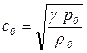 , (5.140)
, (5.140)
где 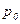 - среднее давление;
- среднее давление;
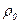 - средняя плотность среды;
- средняя плотность среды;
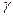 - отношение теплоемкостей при постоянном давлении и объеме.
- отношение теплоемкостей при постоянном давлении и объеме.
Это распространение возмущения сопровождается изменением давления, скорости, плотности, и температуры.
Плоская гармоническая волна
Уравнение для давления плоской синусоидальной волны, распространяющейся вдоль положительного направления оси OX, имеет вид
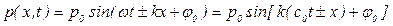 , (5.141)
, (5.141)
где 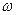 - круговая частота;
- круговая частота;
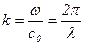 - волновое число (
- волновое число ( 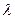 - длина волны);
- длина волны);
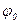 - начальная фаза колебаний точек среды;
- начальная фаза колебаний точек среды;
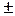 - распространение волны вдоль положительного или отрицательного направления оси OX.
- распространение волны вдоль положительного или отрицательного направления оси OX.
Существует и экспоненциальная форма записи уравнения плоской волны (эквивалентная синусоидальной форме):
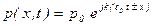 (5.142)
(5.142)
Данная форма записи удобна для дифференцирования.
Получим выражение для скорости волны 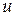 .
.
Для этого используем линеаризованное уравнение динамики (из закона сохранения количества движения, уравнение динамики, связывающее градиент давления 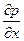 и производную скорости по времени
и производную скорости по времени 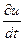 )
)
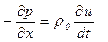 . (5.143)
. (5.143)
Вводя оператор 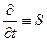 , приходим к удобному выражению
, приходим к удобному выражению
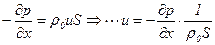 .
.
Отсюда после очередной замены 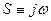 (переходим в частотную область) из (5.144) получим
(переходим в частотную область) из (5.144) получим
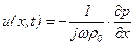 .
.
Продифференцировав (5.142), подставив результат в правую часть последнего выражения и производя последующую замену 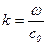 , приходим к выражению
, приходим к выражению
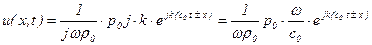 .
.
Перепишем окончательное выражение для скорости
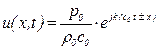 , (5.144)
, (5.144)
которое устанавливает связь между скоростью волны, давлением и плотностью среды.
Переносимая волной интенсивность звука 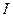 (средний поток звуковой энергии на единицу площади) выражается с помощью осредненного во времени произведения давления на скорость
(средний поток звуковой энергии на единицу площади) выражается с помощью осредненного во времени произведения давления на скорость
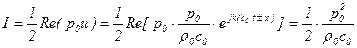 , (5.145)
, (5.145)
где 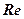 - реальная часть в комплексных выражениях зависимостей.
- реальная часть в комплексных выражениях зависимостей.
Из последнего соотношения следует, что интенсивность звука при распространении волны полностью описывается давлением.
Произвольная плоская волна
Плоскую волну можно получить, возбуждая цилиндрическую трубку конечной длины с помощью поршня, колеблющегося, например, вдоль оси OX.
На торце поршня происходит отражение возмущения, и поле давления можно описать следующим образом по аналогии (5.142)
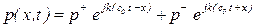 (5.146)
(5.146)
Величины 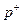 и
и 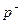 - составные части амплитуды падающего и отраженного волн.
- составные части амплитуды падающего и отраженного волн.
Поле скорости получаем из уравнения динамики (вида 5.144)
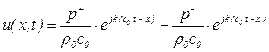 , (5.147)
, (5.147)
Выражения (5.146) и (5.147) показывают, что изменения амплитуды давления 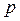 и скорости
и скорости 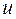 происходят не синфазно, а зависят от абсциссы x.
происходят не синфазно, а зависят от абсциссы x.
Интенсивность 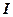 вычисляется по выражению (по аналогии (5.145))
вычисляется по выражению (по аналогии (5.145))
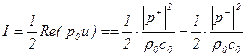 , (5.148)
, (5.148)
Как следует из последнего выражения, значение интенсивности не зависит от x и представляет собой разность между падающим и отраженным потоками.
5.12.2. Распространение трехмерной волны
Волны в этом случае не являются плоскими и происходит уменьшение амплитуды с увеличением расстояния от источника до точки наблюдения (что следует из закона сохранения энергии).
Рассмотрим случай сферического источника с пульсирующим потоком энергии 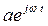 .
.
В этом случае имеют место следующие соотношения:
- давление
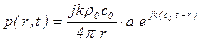 ; (5.149)
; (5.149)
- скорость
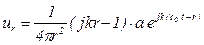 , (5.150)
, (5.150)
- интенсивность
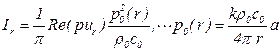 , (5.151)
, (5.151)
Из этих выражений видно, что радиальная составляющая интенсивности убывает обратно пропорционально квадрату расстояния от источника при любых 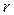 .
.
5.12.3. Микрофоны
Из названных в предыдущих разделах механических величин, характеризующих звуковые волны можно измерить только давление, а скорости частиц, соответствующие звуковым волнам, слишком малы и, следовательно, их нельзя измерить обычными анемометрами, используемых при исследовании жидкостей.
Однако компоненты скорости звука можно определить косвенным образом с использованием уравнения динамики, связывающего градиент давления и производную скорости по времени (см. (5.143))
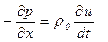 .
.
Эту операцию можно произвести, используя датчик, применяемый для измерения разности давлений. Этот датчик, основанный на измерении градиента давления, называется микрофоном.
Другой часто используемый метод состоит в обработке с помощью электроники разности сигналов с двух микрофонов.
5.12.3.1. Принцип действия микрофона
Микрофон представляет собой датчик, преобразующий акустический сигнал в электрический.
Классическим можно считать микрофон, применяемый в телефонной трубке.
Основан на необратимом явлении, под действием давления происходит изменение сопротивления контакта частиц угля, заполняющих объем, закрытый мембраной.
Но микрофон этого типа не приспособлен для физических измерений, т.к. имеет ограниченную полосу пропускания.
Для создания измерительных микрофонов предпочтительнее методы преобразования, основанные на обратимых явлениях электромагнитного, электростатического, пьезоэлектрического типов.
5.12.3.2. Основные типы микрофонов
Выделяются группы микрофонов, предназначенных для измерения:
- давления;
- градиента давления.
Первые осуществляют физические измерения давления, вторые - физические измерения скорости звука.
Важное преимущество последних – их чувствительность к направлению распространения.
Для получения более выраженной направленности можно использовать микрофоны, чувствительные ко второму градиенту.
 5.12.3.3. Электро-механо-акустические аналоги
5.12.3.3. Электро-механо-акустические аналоги
Аналогия “течение – ток”
Сопоставляя уравнения для электрических цепей и уравнения акустических явлений, можно обнаружить некоторые аналогии.
Рассмотрим акустическую схему – простой акустический контур, представленный на рисунке 5.44.
На рисунке:
1- капиллярный канал;
2- полость объема V;
3- трубка с площадью сечения A;
u – скорость, p – давление.
Поскольку равенство давлений 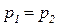 по разные стороны разграничивающих плоскостей означает равенство плотностей, из закона сохранения массы вытекает, что расход, вычисляемый как
по разные стороны разграничивающих плоскостей означает равенство плотностей, из закона сохранения массы вытекает, что расход, вычисляемый как
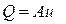 , (5.152)
, (5.152)
при переходе через эти плоскости сохраняется (т.е. течение сохраняется). Это течение можно рассматривать как аналог электрического тока, т.е. можно утверждать
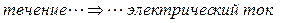 .
.
Аналогия акустической массы
Находящийся в трубе газ массой 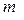 перемещается как целое под действием разности давлений
перемещается как целое под действием разности давлений 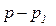 . Тогда справедливы соотношения
. Тогда справедливы соотношения
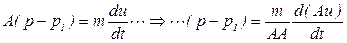 ,
,
откуда
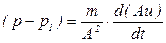 (5.153)
(5.153)
где 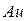 - расход газа.
- расход газа.
Приведем уравнение основного закона механики (динамики) имеет вид
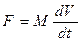 , (5.154)
, (5.154)
где 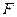 - сила, действующее на твердое тело с массой
- сила, действующее на твердое тело с массой 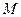 , под действием которой оно движется со скоростью
, под действием которой оно движется со скоростью 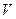 .
.
Также известно выражение для закона Ома
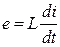 , (5.155)
, (5.155)
в котором 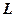 - индуктивность,
- индуктивность, 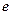 - разность потенциалов,
- разность потенциалов, 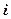 - ток.
- ток.
Как следует из рассмотрения полученных соотношений, уравнение для газа (5.153) близко по форме к уравнению механики (5.154) и выражению закона Ома. Формально сомножитель 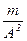 в правой части выражения (5.153) можно интерпретировать как акустическую массу.
в правой части выражения (5.153) можно интерпретировать как акустическую массу.
Таким образом, существует аналогия между механической массой 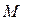 , индуктивностью
, индуктивностью 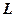 и акустической массой
и акустической массой 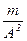 . При этом перемещение массы играет роль тока
. При этом перемещение массы играет роль тока
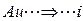 , (5.156)
, (5.156)
а разность давлений - разность потенциалов
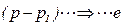 . (5.157)
. (5.157)
Акустическое сопротивление
Падение давления в капилляре, вызванное вязкостью, пропорционально скорости (при ламинарном течении).
Таким образом, получаем
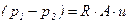 , (5.158)
, (5.158)
где 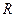 - аналог гидравлического сопротивления, которое называется акустическим сопротивлением.
- аналог гидравлического сопротивления, которое называется акустическим сопротивлением.
Акустическая упругость
Из-за малых размеров сжатие газа в полости происходит без смещения его центра массы. Процесс сжатия описывается законами термодинамики.
Предполагая сжатие адиабатическим (изменение количества теплоты, сообщенное в процессе, отсутствует, при котором можно принять 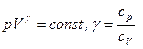 , где
, где 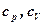 - удельная теплоемкость при постоянном давлении и объеме) получаем
- удельная теплоемкость при постоянном давлении и объеме) получаем
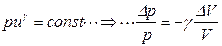 .
.  (5.159)
(5.159)
