Екі вектордың скаляр көбейтіндісі және оның қасиеттері
Вектордың векторлық проекциясы және оның қаситеттері.
Вектордың проекциясы келесі қасиеттерге ие:
1) Прb(a1+ a2) =Прba1+ Прba2(қосындының проекциясы
проекциялардың қосындысына тең);
2)Прb(λa) =λПрba (векторды санға көбейтіндісінің
Проекциясы вектордың проекциясын осы санға көбейткенге тең).
Анықтама. 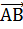 векторының l осіне түсірілген векторлық проекциясы деп
векторының l осіне түсірілген векторлық проекциясы деп 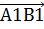
векторын атайды.Мұндағы А1 нүктесі 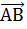 векторының l осіне түсірілген бастапқы А нүктесінің проекциясы, ал В1нүктесі оның В нүктесінің проекциясы және былай
векторының l осіне түсірілген бастапқы А нүктесінің проекциясы, ал В1нүктесі оның В нүктесінің проекциясы және былай
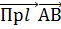 белгілейді.
белгілейді.
Екі вектордың скаляр көбейтіндісі және оның қасиеттері
Екі вектордың ұзындықтарының көбейтіндісін
олардың арасындағы бұрыштың косинусына көбейткенде пайда
болған шаманы олардың скаляр көбейтіндісідеп атаймыз. a жəне b
векторларының скаляр көбейтіндісін
(a, b )[немесе a* b; немесе ab] арқылы белгілейді. Егер 𝝋– a жəне b векторларының арасындағы бұрыш болса, онда
(a, b ) =| a|*|b| *cos𝝋
Скаляр көбейтінді келесі қасиеттерге ие:
1) (a,b ) = (b,a)(коммутативтілік).
2) (a,a) = |a |2 (вектордың скаляр квадраты оның ұзындығының
квадратына тең)
3) Скаляр көбейтінді нөлге тең сонда тек сонда ғана, егер
көбейткіштерортогоналнемесеолардыңеңбомағандабірі
нөлдік вектор болғанда.
4) (a, b) = |b|Прba= |a|Прab
5) (a+b,c)= (c,a)+(c,b)
6) (λa, b ) = λ(a, b )
№5 қасиетті дәлелдеу: (a+b,c)=(a+b)*(c)*cos(a+b,^c)=|c|*Прc(a+b)=|c|*(Прсa+Прсв)=|c|*|a|*cos (a,^c)+|c|*|b|*cos(c,^b)=(c,a)+(c,b).
11. Векторлардың векторлық көбейтіндісі және оның геометриялық мағынасы.Егер а, b, с оң қолдың баспармақ , сұқ саусақ, ортаңғы саусақ тарға сәйкес орналасса, онда а, b, c үштігін оң деп атаймыз, кез келген 3 вектордан 6 үштік құрауға болады:
Егер үштікте 2 вектордың орнын ауыстырса, үштік атын өзгертеді,
a, b, c; a, c, b; …..
Анықтама. а және в векторының векторлық көбейтіндісі деп келесі шартты қанағаттандыратын с векторын айтамыз:
1) а, в, с-оң үштік
2)а перпендук с, в перпендукляр с
3)|с|=|[a,b]|=|a||b|sin(a,b) c=[a,b]
a,bвекторларының векторлық көбейтіндісініңқасиеттері:
1)кез келген a,b [a,b]=-[b,a]
2 кез келген a,bкез келген α€IR [αa,b]=α[a,b]
3)[λa,b]=[a,λb]=λ[a,b]
4)[a,a]=0≠a2
Теоремасы : а={x1, y1, z1} b={x2, y2, z2}
Декарт координаттар жүйесінде а мен б-ның векторлық көбейтіндісі келесі формула бойынша есептеледі:
[a,b]= 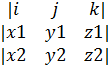
Геометриялық мағынасы – сол вектордан құралған паралелограмның ауданына тең. S=|a||b|sin(a,b)=|[a,b]|
Теорема:Ө емес а, б вектор-ң векторлық көбейтіндісі 0-ге тең болады, сонда және сонда ғана егерде олар коллинеар. Коллениар векторлар арасындағы бұрыш 0 градусқа неемесе 180 градусқа тең.
[ 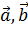 ]=Ө =>
]=Ө => 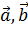 – коллениар
– коллениар
Д/У: [ 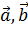 ]=Ө => |[
]=Ө => |[ 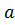 ,b]|=|a||b|sin(a,b) =0
,b]|=|a||b|sin(a,b) =0
1. 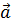 =Ө немесе
=Ө немесе 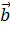 =Ө нөлдік вектор кез келген векторға коллениар.
=Ө нөлдік вектор кез келген векторға коллениар.
2. sin(a,b) =0=> (a^b)= π немесе(a^b)=0 векторлар параллел онда олар коллениар.
12. Векторлардың аралас көбейтіндісі және оның геометриялық мағынасы. Векторлардың аралас көбейтіндінің есептеу формуласы. (дәлелдеумен)
Үш вектордың аралас көбейтіндісі.Анықтама.Ретке келтірілген нөлдік емес a,b,c векторлары үштігінің аралас көбейтіндісі деп a*b векторымен c векторының скалярлық көбейтіндісіне тең санды айтады. Үш вектордың аралас көбейтіндісі a*b*c деп белгіленеді. Сонда, анықтама бойынша,а*b*c =(a*b)*c .
Егер a,b,с векторларының кем дегенде біреуі нөлдік вектор болса,онда аралас көбейтінді нөлге тең деп саналады.
Геометриялық мағынасы. 1-теорема. Компланар емес a,b,c векторларының көбейтіндісі ортақ бас нүктеден шыққан a,b,c векторларына салынған, егер a,b,c векторлар үштігі оң жақты болса,онда оң таңбамен,ал a,b,c үштігі сол жақты болса,теріс таңбамен алынған параллелепипедтің көлеміне тең болады. A,b,c векторлары компланар емес деп санап, мына екі жағдайды қарастырамыз. Алдымен, a,b,c үштігі оң жақты деп санайық.
А=OA, b=OB, c=OC векторларына салынған параллелепипедтің көлемін V арқылы белгілейік. Сонда V=S*h.
Мұндағы S a және b векторларына салынған параллелограмның ауданы,ал h=\OD\-параллепипедтің биіктігі. A*b=d деп белгілейік. Екі вектордың векторлық көбейтіндісінің анықтамасы бойынша;1\ \d\=s;
2\d векторы а және b векторлары жүргізілген жазықтығына перпендикуляр;
3\a,b,d векторлар үштігі оң жақты болады. Бұдан с және d векторлары жазықтығының бір жағында оорналасқандығы шығады,демек
OCD үшбұрышынан h=\c\*cosµ \1\
Енді d және с векторларының скаляр көбейтіндісін қарастырайық. Сонда ол бір жағынан d*c=(a*b)*c \2\
болса, ал екінші жағынан ,|d|=s теңдігі мен формуланы пайдалансақ,онда
d*c=|d|*|c|*cosµ=S*h=V \3\
болады,\2\ және\3\-формулалардың оң жақтарын теңестірсек,(a*b)*c=V болады.
Енді a,b,c векторлар үштігі сол жақты деп санайық. Сонда a*b=d және с векторлары α жазықтығының әртүрлі жағында жатады,демек,(c^,d)=µ>∏/2, яғни,соsµ< 0. OCD үшбұрышынан мына теңдік шығады. h=|c|*cosµ=|c|*cos(∏-µ)=-|c|*cosµ \4\
Егер |d|=S және \4\ формулаларын ескерсек,онда d*c=|d|*|c|*cosµ=S*(-h)=-S*h=-V \5\
Ал,егер a,b,c векторлар үштігі сол жақты болса, онда \2\ және \5\ формулалардан мына формуланы шығарып аламыз. (a*b)*c=-V. Сонымен, кез келген компланар емес a,b,c векторлар үштігі үшін V=|(a*b)c| формуласын аламыз.
Есептеy формаласы:
ТКЖ:a=(a1,a2,a3), b( b1,b2,b3)
i, j,k-орта нормаланған базис
[a,b]= 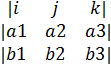 =i*|
=i*| 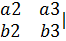 -j
-j 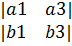 +K
+K 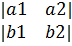
[a,b]=(a2b3-b2a3-a1b3+b1a3*a1b2-b1a2) S= 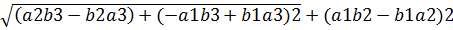
C=(c1,c2,c3) a=(a1,a2,a3) b=(b1,b2,b3)
(a, b ,c)= 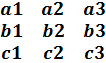
Жазықтықтағы түзулердің параметрлік, канондік теңдеулерін қорытып шығару. Жазықтықтағы түзудің жалпы теңдеуі.
Мына есепті шығарайық:бағыттаушы векторы 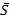 =(l,m)–ке тең,берілгенM˳(x˳,y˳) нүктесін басып өтетін d түзуінің теңдеуін табыңдар.M(x,y)
=(l,m)–ке тең,берілгенM˳(x˳,y˳) нүктесін басып өтетін d түзуінің теңдеуін табыңдар.M(x,y) 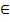 d нүкте болсын,сонда
d нүкте болсын,сонда 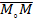 =(x-x˳,y-y˳). Cондықтан
=(x-x˳,y-y˳). Cондықтан 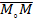 ||
|| 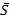 /1/,бұдан
/1/,бұдан 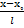 =
= 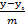 - (канондық теңдеу), яғни кез-келген нүктесінің M(x,y)
- (канондық теңдеу), яғни кез-келген нүктесінің M(x,y) 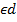 координаталары /1/- теңдеуді қанағаттандырады.
координаталары /1/- теңдеуді қанағаттандырады.
Керісінше ,M*(x*,y*) нүктесі,координаталары \1\ теңдеуді қанағаттандыратын нүкте болсын,яғни 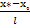 =
= 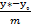 . Олай болса,
. Олай болса, 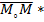 =(x*-x˳,y*-y˳)және
=(x*-x˳,y*-y˳)және 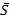 =(l,m) векторлары коллинеар болады,демекM*(x*,y*)
=(l,m) векторлары коллинеар болады,демекM*(x*,y*) 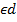 . Сөйтіп /1/ -теңдеу іздеген теңдеуіміз болып шықты. Бұл теңдеу түзудің канондық теңдеуі деп аталады. /2/-формуладағы бөлшектердің біреуінің бөлімі нөлге айналуы мүмкін. /әрине
. Сөйтіп /1/ -теңдеу іздеген теңдеуіміз болып шықты. Бұл теңдеу түзудің канондық теңдеуі деп аталады. /2/-формуладағы бөлшектердің біреуінің бөлімі нөлге айналуы мүмкін. /әрине 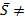 0 болғандықтан екі бөлшектердің бөлімдері бір уақытта нөлге тең болмайды. Бұл жағдайда,
0 болғандықтан екі бөлшектердің бөлімдері бір уақытта нөлге тең болмайды. Бұл жағдайда, 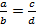 пропорциясын ad=bc теңдігінің орындалуын пара-пар деп түсінгендіктен,ол бөлшектің сәйкес алымын нөлге тнң деп санаймыз.
пропорциясын ad=bc теңдігінің орындалуын пара-пар деп түсінгендіктен,ол бөлшектің сәйкес алымын нөлге тнң деп санаймыз.
/1/теңдеудегі теңдіктің оң және сол жағындағы бқлшектердің жалпы мәнін t деп белгілейік. Сонда t парметрінің өзгеру облысының барлық сан осі (R) болатынына көз жеткізу қиын емес.
Шынында да,бөлшектердің кемінде біреуіңің бөлімі нөлге тең емес,демек,бөлшектің сәйкес алымы кез-келген мәнді хабарлай алады. Олай болса t 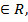 яғни -
яғни - 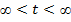 Сонымен /1/-теңдеуден немесе теңдеулерін аламыз.
Сонымен /1/-теңдеуден немесе теңдеулерін аламыз.
x-x˳=lt , y-y˳=mt немесе 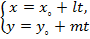 \2\
\2\
/2/-теңдеулер түзудің парметрлік теңдеулері деп аталады.
Анықтама(Жазықтықтағы түзудің жалпы теңдеуі.).Ax+By+C=0 \1\ теңдеу түзудің жалпы теңдеуі деп аталады.
1-теорема.Жалпы теңдеуі арқылы анықталған түзуі,сол түзудің нормалдық векторы деп аталатын n=(A,B) векторына перпендикуляр болады.\1\ теңдеу кем дегенде бір (x˳,y˳) шешімі бар болатынын тексеру қиын емес.Шынында да,A және B коэффициенттері бір уақытта нөлге айналмайтын болғандықтан,A≠0 деп алайық.Егер y=y˳ десек,онда \1\ теңдеуден мына мәнді шығарамыз: x˳=-(B/A)y˳-(C/A).Демек,Ax˳+By˳+C=0 \2\
теңбе-теңдігі орындалатындай M˳(x˳y˳) нүктесі табылады.Егер \1\ теңдеуден \2\ теңбе-теңдігін мүшелеп алып тастасақ,онда \1\ теңдеуге мәндес мына теңдеуді аламыз:A(x-x˳)+B(y-y˳)=0 \3\.
\3\ шарт d түзуінде жатқан кез келген M˳M=(x-x˳,y-y˳)векторы мен n=(A,B) векторының перпендикулярлық (ортоганалдық) шартын (белгісін) көрсетеді.
2-анықтама./3/-теңдеу M˳(x˳,y˳) нүктесі арқылы өтетін. 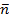 =(a,b) векторына перпендикуляр түзу теңдеуі деп аталады.
=(a,b) векторына перпендикуляр түзу теңдеуі деп аталады.
2-теорема. Нөлдік емес 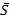 =(l,m) векторы /1/-жалпы теңдеумен берілген d түзуінің бағыттаушы векторы үшін Al+bm=0 \4\ шартының орындалуы қажетті және жеткілікті.
=(l,m) векторы /1/-жалпы теңдеумен берілген d түзуінің бағыттаушы векторы үшін Al+bm=0 \4\ шартының орындалуы қажетті және жеткілікті.
Қажеттілік. 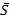 =(l,m)
=(l,m) 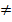 0 векторы
0 векторы
Ax+by+c=0, 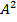 +
+ 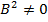
tеңдеуімен анықталған d түзуінің бағыттаушы векторы дейік. 1-теорема негізінде 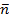 =(A,B)
=(A,B) 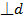 болады. Бұдан.
болады. Бұдан. 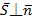 демек,бұл екі вектордың скалярлық көбейтіндісі нөлге тең,яғни
демек,бұл екі вектордың скалярлық көбейтіндісі нөлге тең,яғни 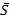 *
* 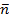 =A*l+ B*m=0. Қысқаша: s векторы d түзуінің бағыттаушы векторы болғандықтан,
=A*l+ B*m=0. Қысқаша: s векторы d түзуінің бағыттаушы векторы болғандықтан, 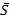 *
* 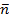 =A*l+ B*m=0
=A*l+ B*m=0
Жеткіліктілік. Al+bm=0 болсын. Сонда 0= Al+bm= 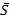 *
* 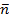 ↔
↔ 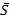 ||d
||d 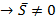
Яғни,анықтама бойынша s векторы d түзуінің бағыттаушы векторы болады.
Салдар. 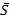 =(-B,A)векторы жалпы теңдеуімен анықталған d түзуінің бағыттаушы векторы болады. Шынында да, S=(-B,A) векторы үшін /4/-шарт орындалады.
=(-B,A)векторы жалпы теңдеуімен анықталған d түзуінің бағыттаушы векторы болады. Шынында да, S=(-B,A) векторы үшін /4/-шарт орындалады.
14. Жазықтықтағы екі түзудің өзара орналасуы және жазықтықтағы екі түзудің арасындағы бұрыш. (дәлелдеумен)
1-теорема.
P₁:A₁x+B₁y+C=0
p₂:A₂x+B₂y+C=0
1) P₁ мен p₂ түзулері беттеседі сжтсғ,егер де олардың теңдеулеріндегі барлық коэффиценттер пропоционал болса.
1) P₁ 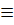 p₂
p₂ 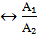 =
= 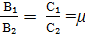 ,
, 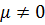
2)мен түзулерінің қиылысуы бос жиын болады, сжтсғ, егер олардың теңдеулеріндегі х пен у-тің алдындағы коэфф, пропоционал болып, үшінші коэф-і пропоционал болмаса
2) P₁ 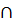 p₂
p₂ 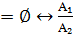 =
= 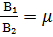 ,
, 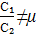
3)мен түзулері жалғыз нүктеде қиылысады, сжтсғ, егер олрадың теңдеулеріндегі х пен у-тің алдындағы коэф-і пропоционал емес болса
3) P₁ 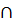 p₂=(.)
p₂=(.) 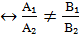
Формулалар(және жазықтықтағы екі түзудің арасындағы бұрыш)
1) p₁: x=x₁+l₁t
y=y₁+m₁t , 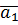 =(l₁m₁)
=(l₁m₁)
p₂: x=x₂+l₂t
y=y₂+m₂t , 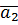 =(l₂m₂)
=(l₂m₂)
tg(p₁^p₂)=tg( 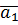 ^
^ 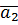 )=
)= 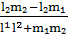
2) P₁:A₁x+B₁y+C=0 , 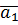 =(-B₁,A₁)
=(-B₁,A₁)
p₂:A₂x+B₂y+C=0 , 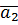 =(-B₂,A₂)
=(-B₂,A₂)
tg(p₁^p₂)= 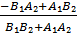
3)p₁:y=k₁x+b₁ , 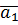 =(1,k₁)
=(1,k₁)
p₂:y=k₂x+b₂, 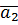 =(1, k₂)
=(1, k₂)
tg (p₁^p₂)= 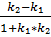
Ескерту! 1) p₁⏊p₂↔l₁l₂+m₁m₂=0
A₁A₂+B₁B₂=0
1+k₁*k₂=0, k₂=- - 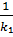
2)p₁ 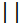 p₂↔
p₂↔ 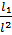 =
= 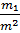 ,
,
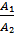 =
= 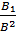 , k₂=k₁
, k₂=k₁
