Матрицаның қасиеттері

1. Бірдей өлшемді A=(aij) және B=(bij) матрицаларының қосындысы сондай өлшемді C=(cij) матрица болады. Оның элементтері келесі теңдікпен анықталады:

aij+bij=cij(i=1,2,…,m; j=1,2,…,n)

Белгіленуі: А+В=С

2. А=(аij) матрицасын к санына көбейту, әрбір элементі А матрицасының сәйкес элементтері мен к санының көбейтіндісі болатын матрица болады:

K=k(aij) (i=1,2,…,m; j=1,2,…,n).

3. Amxk матрицасын Вkxn матрицасына көбейту (яғни, бірінші көбейткіштің бағандар саны екінші көбейткіштің жолдар санына тең) Сmxn матрицасы болады. Оның элементтері А матрицасының і-ші жолдары мен В матрицасының j-ші бағандарының көбейтіндісінің қосындысы болатын Сij элементтері, яғни:

cij=ai1b1j+ai2b2j+...+aikbkj (i=1,2,…,m; j=1,2,…,n)

4. Кез келген ретті квадрат матрицаны сәйкес бірлік матрицаға көбейту матрицаны өзгертпейді.

8.Кері матрица. Кері матрицаны есептеу тәсілдері.

Нұқсансыз(detA=0) матрицалардың және тек қана солардың кері матрицалары бар. Кері матрица 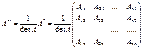формуласы арқылы табылады. Мұндағы А*- қосалқы матрица. Аnxn=(aij) квадрат матрицасы берілсе, оның аijэлементтерінің алгебралық Аij толықтауыштарынан құралған матрицаны қосалқы матрица деп атайды.

9. Матрицаны элементар түрлендіру.Матрицаның рангі және оны есептеу.

А матрицасының рангі деп осы матрицаның нөлге тең емес минорларының ең үлкен ретін айтады және оны r(A) немесе rA немесе rangA символдарының біреуімен белгілейді.

Нөл матрицаның ранг нөлге тең деп есептеледі.

І-әдіс: Көмкеруші минорлар әдісі.

Кез келген –ші ретті нөлге тең емес минор алынады, ал оны ∆1 деп белгілейміз. Енді ∆1-ді көмкеруші барлық 2-ші ретті минорлар қарастырылады. Егер оның барлығы нөлге тең болса, онда r(A)=1, ал егер олай болмаса, яғни ең болмағанда нөлге тең емес екінші ретті бір минор бар болса, онда оны ∆2арқылы белгілейміз. Келесі циклдер осы сияқты жалғасады. А матрицасының k-ші ретті нөлге тең емес миноры ∆k, ал оны көмкеретін барлық минорлар нұқсанды болса, онда r(A)= ∆k, ал k, ал егер олай болмаса, ∆k+1нөлге тең емес минорын алып, процесс одан әрі жалғасады.

Мратрица рангін табудың тағы бір әдісі – элементар түрлендірулер әдісі, немесе Гаусс әдісі.

1. Жолдардың немесе бағандардың өзара орындарын алмастыру.

2. Қатарды нөл немесе санға көбейту.

3. Қатарға оған паралель қатарды қандай да бір k санына көбейтіп қосу.

4. Нөлдік қатарды алып тастау.

Матрицаға жасалған элементер түрлендірулер оның рангін өзгертпейді.

10. Екінші және үшінші ретті анықтауыштар.

1. Матрицаға сәйкес екінші ретті анықтауыш деп a1b2 – a2b1санын айтады.

Анықтауыш D әрпімен немесе ∆-дельта әрпімен белгіленеді. Сонымен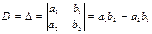

a1,b2 – анықтауыштың бірінші жолының элементтері, а2,b2 – анықауыштың екінші жолының элементтері , а1,а2 – анықтауыштың бірінші бағанының элементтері, b1,b2 – анықтауыштың екінші бағанының эленттері, а1,b2 – бас диагональ элементтері , а2,b1 – қосалқы диагональ элементтері.

матрицаға сәйкес 3-ші ретті анықтауыш деп, 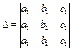символымен белгіленген және ∆=a1b1c1+b1c2a3+a2b3c1-a3b2c1-b3c2a1-a2b1c3 теңдігімен анықталған санды айтады.

11.п-ші ретті анықтауыштар және олардың қасиеттері.

А= 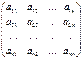матрицасынын анықтаушы деп жіктелу туралы 7 қасиетті және анықтауштың басқа да қасиеттерін пайдалана отырып алынған келесі символымен берілген санды айтамыз :∆=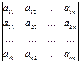

2. Анықтауыштардың қасиеттері. Бұл қасиеттер, 2-ші реттен бастап, кез келген ретті анықтауыштарға тән. Тек үшінші ретті анықтауыштар үшін қарастырайық.

1⁰. Егер анықтауыштың жолдары мен бағандарын ауыстырсақ, анықтауыштың мәні өзгермейді, яғни

a1 b1 с1

a1 a2 a3

a₂ b₂ с₂ b₁ b₂ b₃

a3 b3 с3

с1 с2 с3

2⁰. Анықтауыштың екі қатарының орындарын ауыстыру анықтауышты (-1)-ге көбейткенге тең, яғни:

a1 b1 с1

с1 b1 a1

a₂ b₂ с₂ = с₂ b₂ a₂

a3 b3 с3

с3 b3 a3

3⁰. Егер анқтауыштың екі қатары бірдей болса, онда анықтауыштың мәні нольге тең, яғни:

a₁ b₁ с₁

a₁ b₁ с₁ =0

a₃ b₃ с₃

4⁰. Анықтауыштың қандай да бір қатарының барлық элементтерін кез келген k санына көбейту, анықтауышты осы k санына көбейткенге тең, яғни:

ka1 b1 с1		a1 b1 с1
ka2	b2 с2	=k	a2	b2 с2
ka3	b3 с3		a3	b3 с3

5⁰. Егер анықтауыштың бір қатарының барлық элементтері нольге тең болса, онда ол анықтауыш та нольге тең. (алдыңғы қасиеттегі k=0 болғанда ).

	ka2 kb2 kc2
нольге тең, яғни	a2	b2	c2	=0.
	a3	b3	c3

6⁰. Егер анықтауыштың параллель екі қатарының элементтері пропорционал болса, онда ол анықтауыштың мәні

7⁰. Анықтауыштың қандай да бір қатарының әрбір элементі екі қосындыдан тұрса, онда анықтауышты екі анықтауыштың қосындысы түрінде көрсетуге болады. Олардың бірінің сәйкес қатарының элементтері бірінші қосылғыштар, ал басқасыныкі – екінші қосылғыштар.

8⁰. Егер анықтауыштың қандай да бір қатарының элементтеріне оған сәйкес параллель қатар элементтерін кез келген ортақ k көбейткішке көбейтіп қоссақ, онда анықтауыштың шамасы өзгермейді, яғни:

	a1+ ka2 b1+kb2 с1+kc2		a1 b1 с1
	a 2	b2	с2	=	a2	b2 с2	.
	a3	b3	с3		a3	b3 с3
(70 және 60 қасиеттер негізінде ).

9⁰. Анықтауыштың мәні қандай да бір қатар элементтері мен олардың алгебралық толықтауыштарының көбейтінділерінің қосындысына тең, яғни келесі теңдік дұрыс:

∆=a1 A1	+b1B1	+c1C1;	∆=a1 A1 + a2 A2	+a3 A3
∆=a2 A2	+b2 B2	+c2C2;	∆=b1B1	+b2 B2	+b3 B3
∆=a3 A3	+b3 B3	+c3C3;	∆=c1C1	+c2C2	+c3C3

Анықтауышты осы формулалардың бірімен жазу, оны қандай да бір жол немесе баған элементтері бойынша жіктеу деп аталады.

10⁰. Анықтауыштың қандай да бір қатарының элементтері мен оған параллель қатардың сәйкес элементтерінің алгебралық толықтауыштарының көбейтіндісінің қосындысы нольге тең, яғни:

a₁ A₂ + b₁B₂ + c₁C₂ = 0.

12)Минорлар және алгебралық толықтауыштар.

Анықтама 3.

3-ші ретті анықтауыштың қандай да бір

элементінің миноры деп, осы элемент орналасқан жол және баған элементтерін сызып тастағанда шыққан екінші ретті анықтауышты айтады. Мәселен, ∆үшінші ретті анықтауыштың

a₁ элементінің миноры │ b₂ c₂│- екінші ретті анықтауыш болады,

│ b₃ c₃│

b₁ элементінің миноры │ a₂ c₂│ - жіне т.с.с.

│ a₃ c₃│

Анықтама 4.Анықтауыштың қандай да бір элементініңалгебралық толықтауышы деп, і –ші жол мен j –ші баған

қиылысында орналасқан осы элементтің ( 1)^{i j} таңбасымен

алынған минорын айтады. Алгебралық толықтауыш элементтіңөзі сияқты үлкен әріппен белгіленеді.

13.Анықтауыштарды есептеу.Лаплас теоремасы

Реттері үлкен анықтауыштарды есептеу қиындыққа келтіреді, сондықтан оларды есептеу үшін анықтауыштардың қасиеттерін қолданады және Лапластың жіктеу теоремасын. Лапластың теоремасы берілген анықтауыштың ретін төмендетеді.

Лаплас теоремасы (Лапластың жіктеу теоремасы). Анықтауыштың кез келген жатық (тік) жолдарының элементтерімен оның алгебралық толықтауыштарының көбейтінділерінің қосындысы осы анықтауыштың мәніне тең, яғни

Кез келген n-ші ретті анықтауыштарды есептеу үшін олардың тік немесе жатық элементтері бойынша жіктеу арқылы есептеуге болады. Бұл әдістің мақсаты – анықтауыштардың ретін төмендету. Лаплас теоремасы реті төртке тең немесе төрттен артық анықтауыштарды есептеуде қолданылады. (7) формуланы қолдану арқылы анықтауыштың ретін бірге төмендете отырып өзімізге белгілі болған үшінші немесе екінші ретті анықтауыштарға келтіруге болады және

a1

b1

c1

h1

b1

c1

a1

h1

c1

a1

b1

h1

∆=

a2

b2

c2

∆x

=

h2

b2

c 2

, ∆y

=

a2

h2

c 2

, ∆z

=

a2

b2

h2

.

a3

b3

c3

H3

b3

c3

a3

h3

c3

a3

b3

h3

анықтауыштың қасиетін пайдаланып жіктейін деп отырған тік немесе жатық жолдын бір элементінен басқасы нөльге айналдыру арқылы есептеуді жеңілдетуге болады.

14.Сызықтық алгебралық теңдеулер жүйесі.

Анықтама. n белгісізі бар m сызықтық алгебралық теңдеулер жүйесі келесі түрде жазылады.

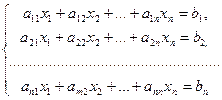мұндағы 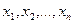-айнымалы жұйенің белгісіздері;

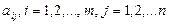-жүйенің коэффенценттері;

Ал 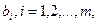-бос мүшелер деп аталады.

Жүйенің барлық теңдеулерін тепе-теңдікке айналдыратын 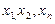сандары жүйенің шешімдері деп аталады.Егер жүйе шешімі бар болса,онда ол үйлесімді,ал егер жүйе шешімі жоқ болса,онда ол үйлесімсіз деп аталады.

15)Сызықты теңдеулер жүйесінің үйлесімді болуының қажетті және жеткілікті шарты(Кроникер-Капелли теоремасы)

Теорема.Сызықтық алгебралық теңдеулер жүйесінің матрицасы мен кеңейтілген матрицасының рангілері тең болса (r(A)=r(Ā)) және тек сонда ғана жүйе үйлесімді болады.

Келесі жағдайлар болуы мүмкін:

1) (r(A)<r(Ā)) Бұл жағдайда Кронекер- Капелли теоремасы бойынша теңдеулер жүйесі үйлесімсіз.

2) r(A)=r(Ā)=r. Бұл жағдайда сол теорема бойынша теңдеулер жүйесі үйлесімді, сонымен бірге:

а)егер r=n болса, яғни матрицалардың рангілері белгісіздер санына тең болса, онда жүйе шешімі жалғыз болады;

б)егер r<n болса, онда теңдеулер жүйесінің n-r параметрлеріне (c₁, c_2,...., c_n-r) тәуелді ақырсыз көп шешімі болады.