Частотные характеристики САУ

Пусть линейная САУ описывается дифференциальным уравнением

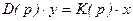, (2.64)
где D(p)=a₀ pⁿ+a₁ p^n-1+...+a_n , K(p)=b₀ p^m+b₁ p^m-1+...+b_m .

Рассмотрим установившийся режим в системе, когда входным воздействием является гармоническая функция времени

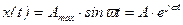, (2.65)

В устойчивой системе, в которой затухает свободная составляющая переходного процесса по истечении достаточно большого промежутка времени, устанавливается периодический процесс той же частоты ϖ, но с другой амплитудой В и фазой j, величина которых зависит от ϖ.

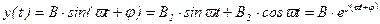, (2.66)

Дифференцируя периодическую функцию 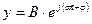получим

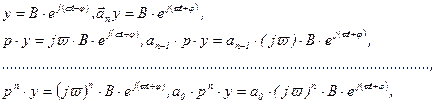
Суммируя полученные равенства почленно, получим

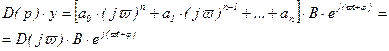, (2.67)

Таким образом, символическое выражение D(p)×y при гармоническом y переходит в алгебраическое комплексное выражение .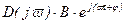

Аналогично

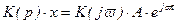, (2.68)

Подставляя (2.67) и (2.68) в (2.64) и сокращая на e^{jϖ t}, найдем

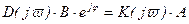, (2.69)

откуда

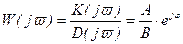, (2.70)
или

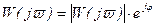, (2.71)

Выражение (2.70) характеризует частотные характеристики системы и называется частотной передаточной функцией или комплексным коэффициентом усиления системы.

Таким образом, комплексным коэффициентом усиления системы (звена) называется отношение комплексной амплитуды сигнала на выходе к комплексной амплитуде сигнала на входе при подаче на вход синусоидального воздействия

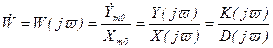, (2.72)

Это комплексное число, модуль которого равен отношению амплитуд выходной и входной величин, а аргумент - сдвигу фаз выходной величины по отношению к входной.

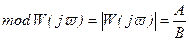, (2.73)

.

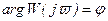Из сравнения выражений для передаточных функций (2.25¸2.28) и комплексного коэффициента усиления легко убедиться, что частотная передаточная функция (комплексный коэффициент усиления) легко получается из обычной путем простой замены p=jϖ.

По аналогии с комплексными числами комплексный коэффициент усиления можно представить в показательной форме или как сумму действительной и мнимой составляющих, то есть

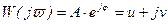, (2.74)

Если изменять частоту входного воздействия ϖ от 0 до ¥, то комплексный коэффициент усиления будет изменяться

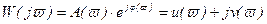, (2.75)

При этом конец вектора W(jϖ) будет скользить по кривой, которая называется частотным годографом комплексного коэффициента усиления или комплексной частотной характеристикой звена, или амплитудно-фазовой частотной характеристикой (АФХ). АФХ строится на комплексной плоскости. По оси абсцисс откладывается вещественная U(ϖ), а по оси ординат мнимая V(ϖ) составляющие комплексного коэффициента усиления. АФХ представляет собой геометрическое место концов векторов (годограф), соответствующих W(jϖ) при изменении частоты от нуля до бесконечности. Для каждой частоты на плоскости соответствует точка. Полученные точки соединяются плавной кривой (рисунок 2.8). АФХ может быть построена как для положительных, так и для отрицательных частот. При замене в частотной передаточной функции +ϖ на -ϖ получится сопряженная комплексная система. Поэтому, АФХ для отрицательных частот может быть построена, как зеркальное изображение относительно вещественной оси АФХ для положительных частот. В большинстве случаев при исследовании САУ ограничиваются построением АФХ для положительных частот.

Вместо АФХ можно построить отдельно амплитудно-частотную характеристику (АЧХ) и фазочастотную характеристику (ФЧХ). Для этого частотную передаточную функцию представляют в показательной форме

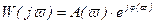, (2.76)

где 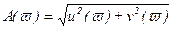- модуль вектора, равный его длине. Это и есть амплитудно-частотная характеристика (АЧХ) (рисунок 2.9).

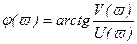- аргумент (фаза) вектора - угол его поворота. Это фазочастотная характеристика (ФЧХ) (рисунок 2.10).

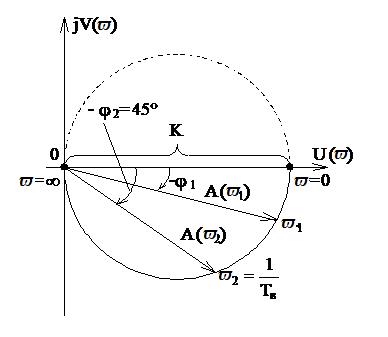
Рисунок 2.8 Амплитудно-фазовая частотная характеристика

Амплитудно-частотная характеристика показывает, как пропускает звено сигналы различной частоты. Оценка пропускания делается по отношению амплитуд выходной и входной величин.

Фазовая частотная характеристика показывает фазовые сдвиги, вносимые звеном (системой) на различных частотах.

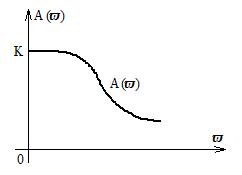
Рисунок 2.9 Амплитудно-частотная характеристика

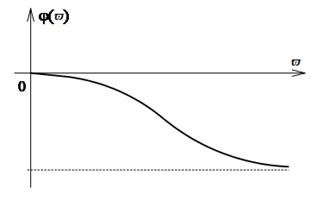
Рисунок 2.10 Фазочастотная характеристика

При исследованиях САУ часто пользуются вещественной и мнимой частотными характеристиками, которые строятся по функциям U(ϖ) (рисунок 2.11) и V(ϖ) (рисунок 2.12).

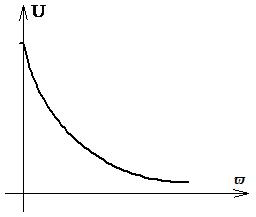
Рисунок 2.11 Вещественная частотная характеристика

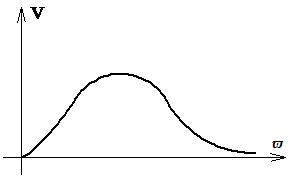
Рисунок 2.12 Мнимая частотная характеристика

Для каждого фиксированного ϖ значение W(jϖ) однозначно определяет точку на комплексной плоскости с декартовыми координатами U(ϖ) и V(ϖ) или полярными координатами А(ϖ) и j(ϖ). Поэтому, легко видеть, что амплитудная, фазовая, вещественная и мнимая частотные характеристики выражаются друг через друга посредством следующих соотношений (рисунок 2.8)

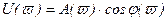, (2.77)

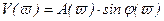, (2.78)
и, наоборот,

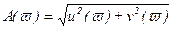, (2.79)

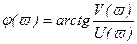, (2.80)

Эти соотношения по сути дела и есть формулы перехода от полярных координат к прямоугольным и, наоборот, от прямоугольных координат к полярным.

Такие системы, в которых функция U(ϖ) однозначно определяет j(ϖ) и, наоборот, функция А(ϖ) однозначно определяет j(ϖ), называются минимально-фазовыми системами.

Исходя из данных выводов и определений, можно предложить простую экспериментальную методику построения АФХ, АЧХ, ФЧХ при синусоидальном входном воздействии. Эта методика хорошо иллюстрирует физический смысл частотных характеристик САУ.

1) На вход исследуемой САУ (звена) подают синусоидальный сигнал с различной частотой ϖ.

2) Для фиксированной частоты ϖ₁ осциллографируют x(t) и y(t) (рисунок 2.13).

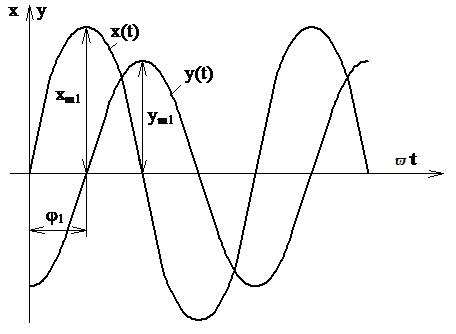
Рисунок 2.13 Гармонический сигнал на входе x(t) и на выходе y(t) САУ

3)Измеряют x_m1, y_m1 и j₁ при w₁

4)Находят 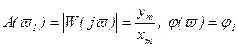и строят одну точку АФХ, АЧХ и ФЧХ (рисунок 2.14).

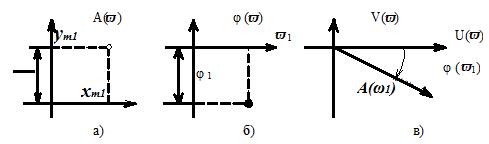
Рисунок 2.14 Экспериментальное построение частотных характеристик:

а - АЧХ, б - ФЧХ, в - АФХ

5) Задают гармонический сигнал с новой частотой v₂ и строят следующую точку характеристики и т.д.

В качестве примера построим частотные характеристики генератора (рисунок 2.14,б).

Для перехода от операторной формы записи (2.35) к частотной передаточной функции достаточно заменить p=jϖ.

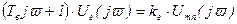, (2.81)

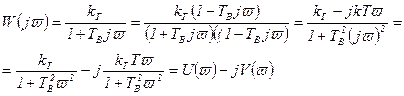, (2.82)

Изменяя ¥> ϖ >0, получим

при ϖ =0: U(ϖ)=K, V(ϖ)=0,

при v=¥: U(ϖ)=0, V(ϖ)=0.

Построение АФХ произведено на рисунке 2.8.

Найдя модуль АФХ, получим амплитудную частотную характеристику.

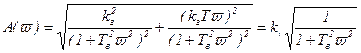, (2.81а)

АЧХ, соответствующая этому выражению, построена на рисунке 2.9.

Построим фазовую частотную характеристику.

,

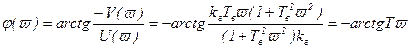(2.83)

График для этой ФЧХ построен на рисунке 2.10.

Определение модуля АФХ (АЧХ) по выражению (2.79) при больших порядках дифференциального уравнения, описывающего поведение координат системы, сопряжено с большими вычислительными трудностями, так как приходится умножать знаменатель и числитель передаточной функции на сопряженное комплексное число, что повышает порядок выражения вдвое.

Трудности, связанные с вычислением амплитудно-частотной характеристики, можно значительно уменьшить, если воспользоваться правилами умножения и деления комплексных чисел. Известно, что при умножении комплексных чисел модули их перемножаются, а аргументы складываются, то есть если z1, z2, ..., zn комплексные числа, то

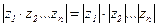, (2.84)

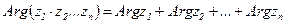, (2.85)

При делении комплексных чисел модуль делимого делится на модуль делителя и из аргумента делимого вычитается аргумент делителя, то есть

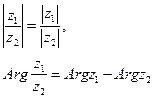(2.86)

Используя эти правила, можно значительно упростить определение модуля АФХ. Например, для АФХ

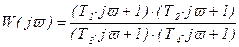, (2.87)

получим

,

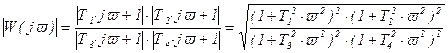(2.88)

,

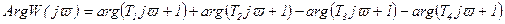(2.89)