Задача 7. Решить смешанную задачу
Уравнения Математической Физики II
11.1. Теоретические вопросы:
1) Основные уравнения. Постановка краевых задач.
2) Решение смешанной задачи для уравнения теплопроводности и волнового уравнения с однородными граничными условиями методом Фурье.
3) Сведение смешанной задачи с неоднородными граничными условиями к задаче с однородными граничными условиями.
4) Решение смешанной задачи для неоднородного уравнения.
5) Уравнение Лапласа. Решение краевых задач для уравнения Лапласа в круге и в круговом секторе методом Фурье.
11.2. Теоретические упражнения :
1) Показать, что функция
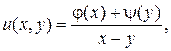

где 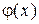 ,
, 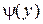 - произвольные непрерывно дифференцируемые функции, является решением уравнения
- произвольные непрерывно дифференцируемые функции, является решением уравнения
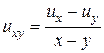 .
.
2) Дан такой однородный стержень с теплоизолированной боковой поверхностью. На его конце x = 0 поддерживается температура, равная нулю, а на конце  температура изменяется по закону
температура изменяется по закону 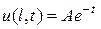 (A-постоянная). Начальная температура
(A-постоянная). Начальная температура 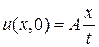 .
.
Найти распределение температуры в стержне t > 0 .
3) Решить задачу об остывании тонкого однородного стержня с теплоизолированной боковой поверхностью, если его начальная температура 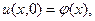 один конец теплоизолирован, а другой поддерживается при постоянной температуре.
один конец теплоизолирован, а другой поддерживается при постоянной температуре.
4) Найти стационарное распределение температуры в кольце, ограниченном двумя концентрическими окружностями, если на каждой из окружностей поддерживается постоянная температура.
5) Найти стационарное распределение температуры в сферическом слое, ограниченном сферами, которые имеют общий центр, если на каждой из сфер поддерживается постоянная температура.
6) Подобрать решение Дирихле
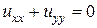
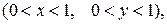

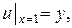

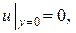
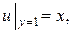
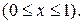
7) Найти гармоническую функцию внутри кругового сектора 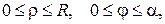 удовлетворяющую граничным условиям
удовлетворяющую граничным условиям 
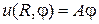 (A-постоянная).
(A-постоянная).
8) Найти решение волнового уравнения типа плоской волны

и сферической волны
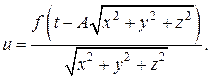
9) Доказать, что если функции  и
и 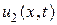 являются решением смешанных задач для одного и того же волнового уравнения с одними и теми же нулевыми граничными условиями и начальными условиями вида соответственно
являются решением смешанных задач для одного и того же волнового уравнения с одними и теми же нулевыми граничными условиями и начальными условиями вида соответственно

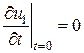
и
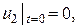
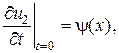
то сумма 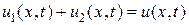 является решением смешанной задачи для этого волнового уравнения с теми же нулевыми граничными условиями и с начальными условиями вида
является решением смешанной задачи для этого волнового уравнения с теми же нулевыми граничными условиями и с начальными условиями вида

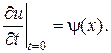
Расчетные задания
Задача 1. Решить смешанную задачу.
1. 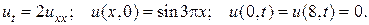
2. 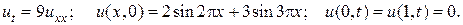
3. 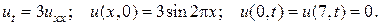
4. 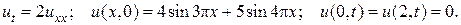
5. 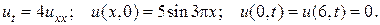
6. 
7. 
8. 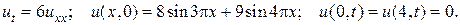
9. 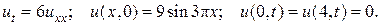
10. 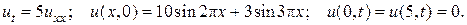
11. 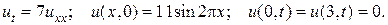
12. 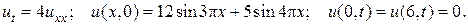
13. 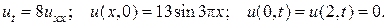
14. 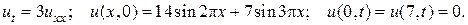
15. 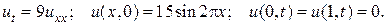
16. 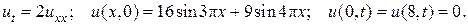
17. 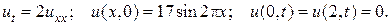
18. 
19. 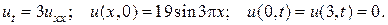
20. 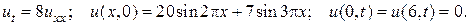
21. 
22. 
23. 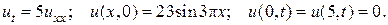
24. 
25. 
26. 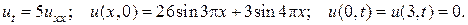
27. 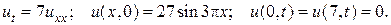
28. 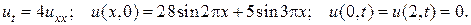
29. 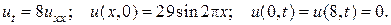
30. 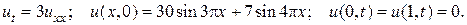
31. 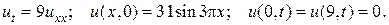
Задача 2. Решить смешанную задачу.
1. 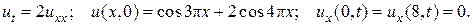
2. 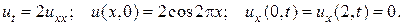
3. 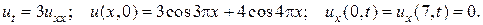
4. 
5. 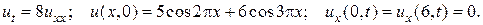
6. 
7. 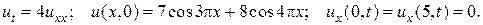
8. 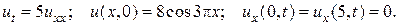
9. 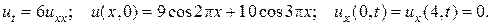
10. 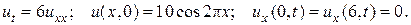
11. 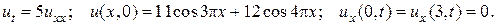
12. 
13. 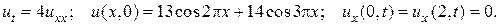
14. 
15. 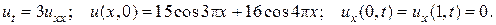
16. 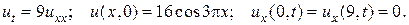
17. 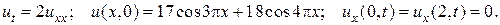
18. 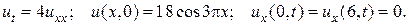
19. 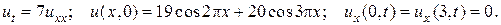
20. 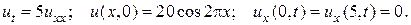
21. 
22. 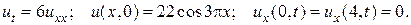
23. 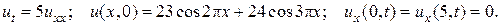
24. 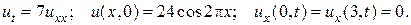
25. 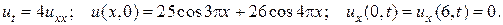
26. 
27. 
28. 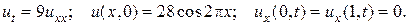
29. 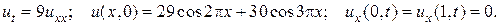
30. 
31. 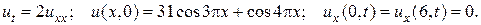
Задача 3. Решить смешанную задачу.
1. 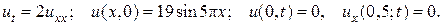
2. 
3. 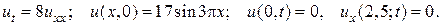
4. 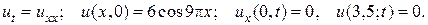
5. 
6. 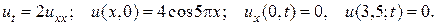
7. 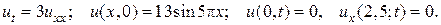
8. 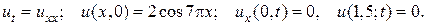
9. 
10. 
11. 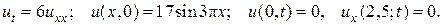
12. 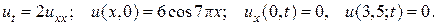
13. 
14. 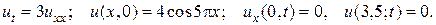
15. 
16. 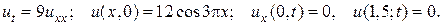
17. 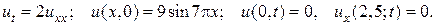
18. 
19. 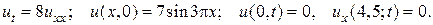
20. 
21. 
22. 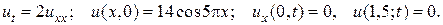
23. 
24. 
25. 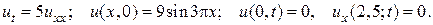
26. 
27. 
28. 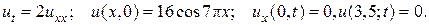
29. 
30. 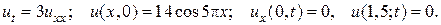
31. 
Задача 4. Решить смешанную задачу.
1. 
2. 
3. 
4. 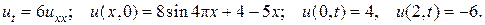
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 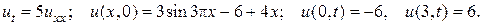
14. 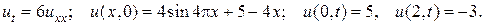
15. 
16. 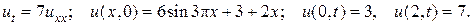
17. 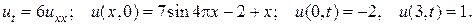
18. 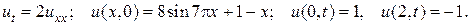
19. 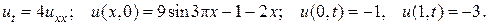
20. 
21. 
22. 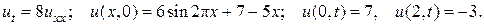
23. 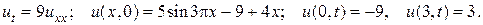
24. 
25. 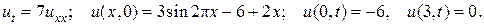
26. 
27. 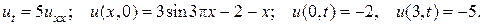
28. 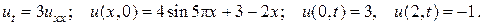
29. 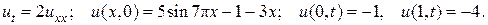
30. 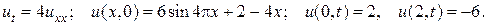
31. 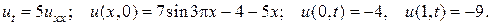
Задача 5. Решить смешанную задачу для данного неоднородного уравнения теплопроводности с нулевым начальным и граничными условиями 
1. 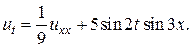 2.
2. 
3. 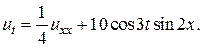 4.
4. 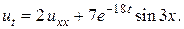
5. 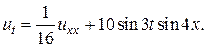 6.
6. 
7. 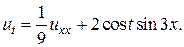 8.
8. 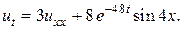
9. 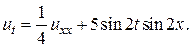 10.
10. 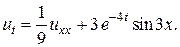
11. 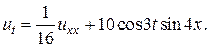 12.
12. 
13.  14.
14. 
15.  16.
16. 
17. 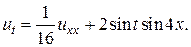 18.
18. 
19.  20.
20. 
21. 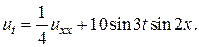 22.
22. 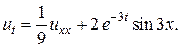
23. 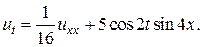 24.
24. 
25. 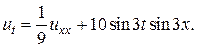 26.
26. 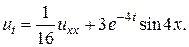
27. 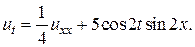 28.
28. 
29.  30.
30. 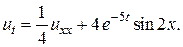
31. 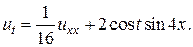
Задача 6. Решить смешанную задачу.
1. 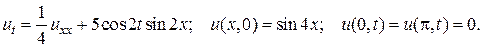
2. 
3. 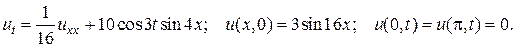
4. 
5. 
6. 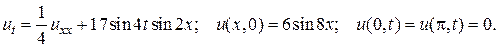
7. 
8. 
9. 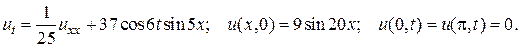
10. 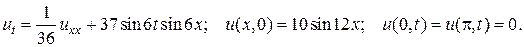
11. 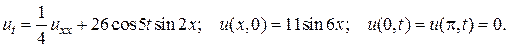
12. 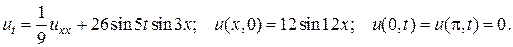
13. 
14. 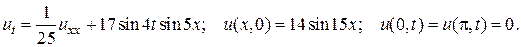
15. 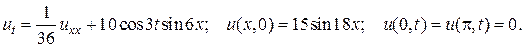
16. 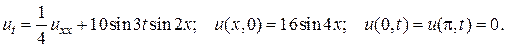
17. 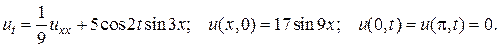
18. 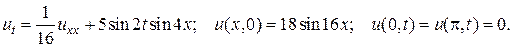
19. 
20. 
21. 
22. 
23. 
24. 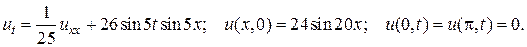
25. 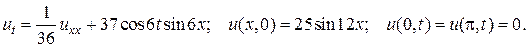
26. 
27. 
28. 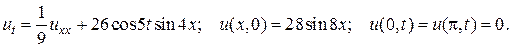
29. 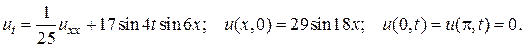
30. 
31. 
Задача 7. Решить смешанную задачу.
1. 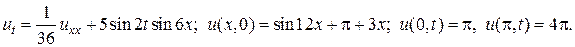
2. 
3. 
4. 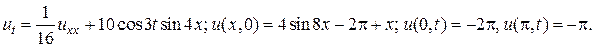
5. 
6. 
7. 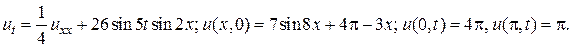
8. 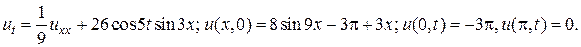
9. 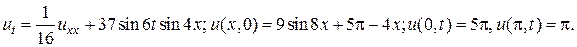
10. 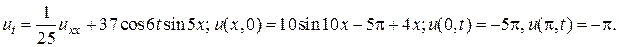
11. 
12. 
13. 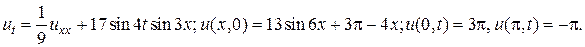
14. 
15. 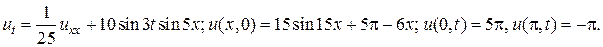
16. 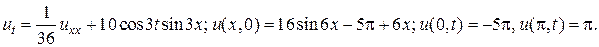
17. 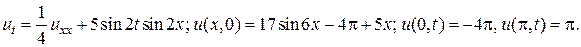
18. 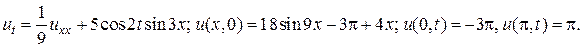
19. 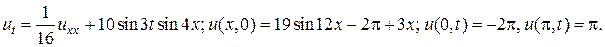
20. 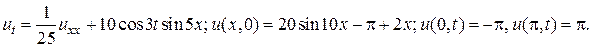
21. 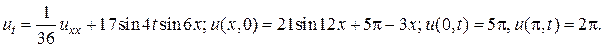
22. 
23. 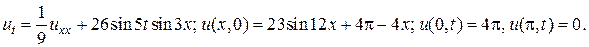
24. 
25. 
26. 
27. 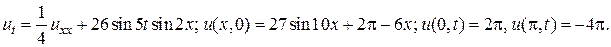
28. 
29. 
30. 
31. 
Задача 8. Найти решение уравнения Лапласа  в круговом секторе
в круговом секторе  ,
,  (
( 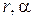 -полярные координаты,
-полярные координаты, 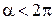 ) , на границе которого искомая функция
) , на границе которого искомая функция 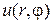 удовлетворяет следующим условиям :
удовлетворяет следующим условиям :
1. 
2. 
3. 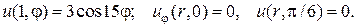
4. 
5. 
6. 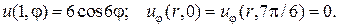
7. 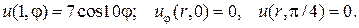
8. 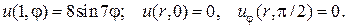
9. 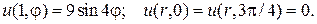
10. 
11. 
12. 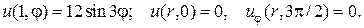
13. 
14. 
15. 
16. 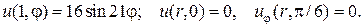
17. 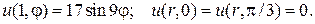
18. 
19. 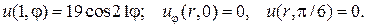
20. 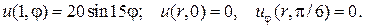
21. 
22. 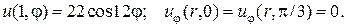
23. 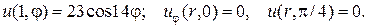
24. 
25. 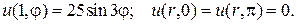
26. 
27. 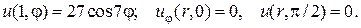
28. 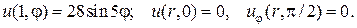
29. 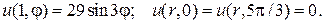
30. 
31. 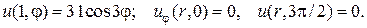
Задача 9. Решить задачу Дирихле для уравнения Лапласа  в круге
в круге 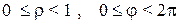 (
(  - полярные координаты), на границе которого искомая функция
- полярные координаты), на границе которого искомая функция  имеет следующие значения :
имеет следующие значения :
1.  2.
2. 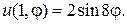
3. 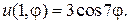 4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11. 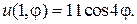 12.
12. 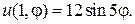
13.  14.
14. 
15.  16.
16. 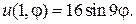
17. 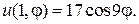 18.
18. 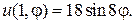
19. 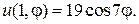 20.
20. 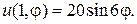
21.  22.
22. 
23.  24.
24. 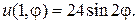
25. 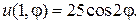 26.
26. 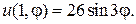
27.  28.
28. 
29. 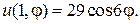 30.
30. 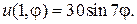
31. 
