Передаточная функция системы

Применение преобразования Лапласа в теории автоматического управления связано с важнейшим понятием – передаточной функцией системы, относящейся к одной из основных характеристик САУ.

Рассмотрим отдельное звено САУ, на вход которого поступает воздействие 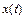, а на выходе формируется сигнал 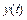(рисунок 1.5).

Рисунок 1.5 – Динамическое звено САУ

Если для сигналов 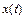, 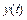существует преобразование Лапласа

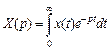и ,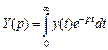

то передаточная функция звена определяется как отношение изображения по Лапласу выходного сигнала к изображению по Лапласу входного сигнала при нулевых начальных условиях:

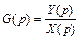. (1.7)

Зная передаточную функцию звена 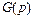и изображение 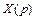входного воздействия 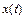, можно найти изображение выходного сигнала звена по соотношению:

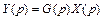. (1.8)

Далее, переходя от изображения 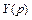к оригиналу 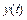, получают процесс изменения выходного сигнала звена при приложении к нему входного воздействия.

Пример 6.Вывести выражение для передаточной функции звена, описываемого дифференциальным уравнением

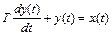
при нулевом начальном условии:

.

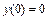Выполним над дифференциальным уравнением преобразование Лапласа:

,

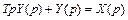откуда найдем передаточную функцию звена по соотношению (1.7):

.

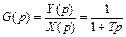Отдельные звенья САУ могут быть соединены друг с другом в различных комбинациях. Зная передаточные функции звеньев, образующих сложную систему c заданной структурной схемой, можно получить передаточную функцию системы в целом, учитывая следующие правила преобразования.