Представлення булевих функцій
Нехай маємо булеву функцію, задану у ДДНФ
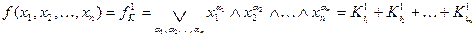 , (1)
, (1)
де 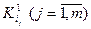 – усі мінтерми функції
– усі мінтерми функції 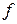 .
.
Побудуємо функцію 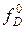 наступним чином:
наступним чином:
1) Запишемо диз’юнкцію усі мінтермів функції 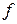 , які не ввійшли формулу (1), тобто, мінтерми функції
, які не ввійшли формулу (1), тобто, мінтерми функції 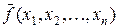 – інверсної до
– інверсної до 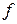 :
:
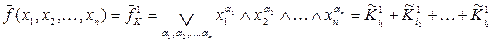 ,
,
де 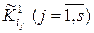 – усі мінтерми функції
– усі мінтерми функції 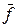 .
.
2) В одержаній формулі замінимо  на
на  ,
, 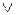 на
на 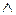 , змінні
, змінні 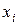 на
на 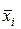 ,
, 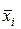 на
на 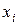 .
.
В результаті такого перетворення дістанемо функцію вигляду
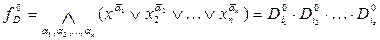 , (2)
, (2)
яка є не що інше як ДКНФ функції 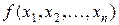 .
.
З формул (1) і (2) випливає рівність
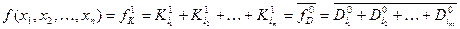 . (3)
. (3)
 Приклад 13. Розглянемо функцію, яка задана таблицею істинності (табл. 18). Користуючись вище описаним алгоритмом, побудувати для неї ДДНФ і ДКНФ.
Приклад 13. Розглянемо функцію, яка задана таблицею істинності (табл. 18). Користуючись вище описаним алгоритмом, побудувати для неї ДДНФ і ДКНФ.
Розв’язання. 1. Запишемо ДДНФ:
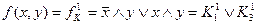 .
.
2. Запишемо диз’юнкцію усі мінтермів функції 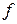 , які не ввійшли формулу
, які не ввійшли формулу 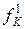 :
:
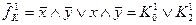 .
.
3. В одержаній формулі виконаємо заміни згідно з п.2 вищенаведеного правила, одержимо функцію
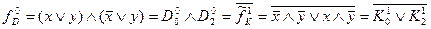 ,
,
яка є не що інше як ДКНФ для функції 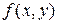 .
.
Зауваження. З одержаних результатів, можна одержати рівності:
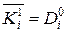 ,
, 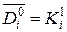 ,
, 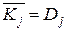 ,
, 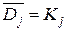 , (4)
, (4)
де 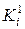 і
і 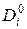 – відповідно мінтерм і макстерм на і-му наборі, а
– відповідно мінтерм і макстерм на і-му наборі, а 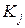 і
і 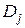 – деякі елементарні кон’юнкціія і диз’юнкція, які одержані одна з одної шляхом заміни
– деякі елементарні кон’юнкціія і диз’юнкція, які одержані одна з одної шляхом заміни 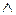 на
на 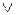 ,
, 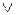 на
на 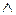 , змінні
, змінні 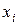 на
на 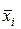 ,
, 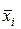 на
на 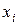 .
.
Означення 1. Форму запису логічних функцій у ДДНФ (ДНФ) будемо називати записом логічної функції у канонічнійдиз’юнктивній нормальній формі або форма І/АБО.
Означення 2. Форму запису логічних функцій у ДКНФ (КНФ) будемо називати записом логічної функції у канонічній кон’юнктивній нормальній формі або форма АБО/І.
Форми І/АБО і АБО/І не є єдними способами задання функції алгебри логіки. Використовуючи закони подвійного заперечення 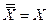 і закони де Моргана
і закони де Моргана 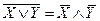 , або
, або 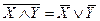 , можна одержати ще шість канонічних форм. Справді, нехай маємо функцію, задану в ДНФ
, можна одержати ще шість канонічних форм. Справді, нехай маємо функцію, задану в ДНФ
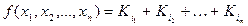 – (форма І/АБО).
– (форма І/АБО).
Використовуючи вищеназвані закони та формули (4), послідовними перетвореннями, одержимо перші чотири канонічні форми:
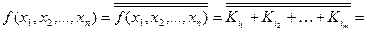
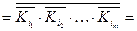 – (форма І-НЕ/І-НЕ)
– (форма І-НЕ/І-НЕ)
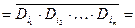 – (форма АБО/І-НЕ)
– (форма АБО/І-НЕ)
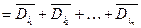 – (форма АБО-НЕ/АБО).
– (форма АБО-НЕ/АБО).
У формі І/АБОможна подати як функцію 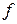 так і її заперечення
так і її заперечення 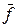 , що дасть ще нові чотири канонічні форми:
, що дасть ще нові чотири канонічні форми:
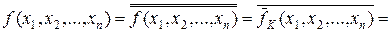
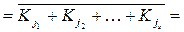 – (форма І/АБО-НЕ)
– (форма І/АБО-НЕ)
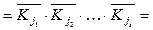 – (форма І-НЕ/І)
– (форма І-НЕ/І)
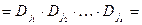 – (форма АБО/І).
– (форма АБО/І).
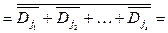 – (форма АБО-НЕ/АБО-НЕ)
– (форма АБО-НЕ/АБО-НЕ)
 Кожна із одержаних форм може бути зручною при побудові логічних схем на конкретних логічних елементах.
Кожна із одержаних форм може бути зручною при побудові логічних схем на конкретних логічних елементах.
Приклад 2. Знайти логічні вирази мажоритарної (порогової) функції від трьох змінних, яка задається таблицею істинності (табл. 2.19).
Розв’язання. Користуючись переходом від табличної форми подання функції алгебри логіки до аналітичної, запишемо її ДДНФ
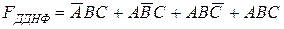 .
.
Виконаємо мінімізацію 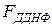 .
.
Застосувавши закон склеювання до першого і четвертого, другого і четвертого, третього і четвертого доданків 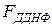 , одержимо:
, одержимо:
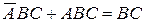 ,
, 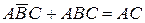 ,
, 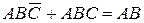 .
.
Таким чином мінімальна форма має вигляд
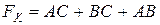 – форма І/АБО.
– форма І/АБО.
Користуючись подвійним запереченням та законом де Моргана, подамо 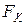 в інших формах:
в інших формах:
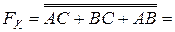
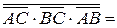 – форма І-НЕ/І-НЕ;
– форма І-НЕ/І-НЕ;
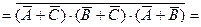 – форма АБО/І-НЕ;
– форма АБО/І-НЕ;
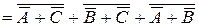 – форма АБО-НЕ/АБО.
– форма АБО-НЕ/АБО.
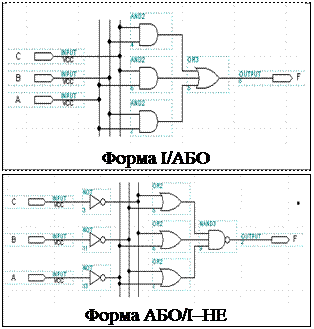
Відповідні логічні схеми та результати моделювання, виконані в системі проектування MAX+PLUS II на базі різних елементів, наведено на рис. 10, 11.
 | |||
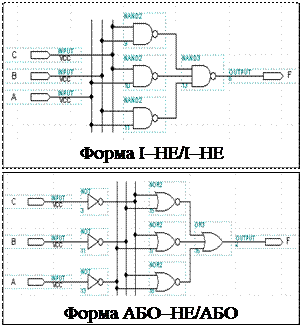 |
Рис. 10
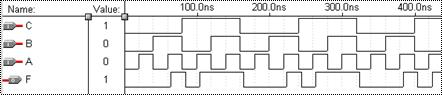
Рис. 11
Для побудови чотирьох інших форм розглянемо функцію 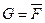 . Користуючись таблицею істинності оберненої функції, знайдемо
. Користуючись таблицею істинності оберненої функції, знайдемо
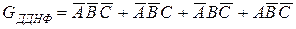 .
.
Застосувавши закон склеювання до першого і другого, першого і третього, першого і четвертого доданків 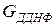 , одержимо
, одержимо 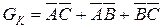 .
.
Оскільки 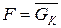 , то маємо:
, то маємо:
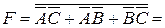 – форма І/АБО-НЕ;
– форма І/АБО-НЕ;
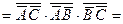 – форма І-НЕ/І;
– форма І-НЕ/І;
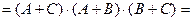 – форма АБО/І;
– форма АБО/І;
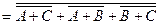 – форма АБО-НЕ/АБО-НЕ.
– форма АБО-НЕ/АБО-НЕ.
Відповідні логічні схеми та результати моделювання, виконані в системі проектування MAX+PLUS II на базі різних елементів наведено на рис. 12, 13.
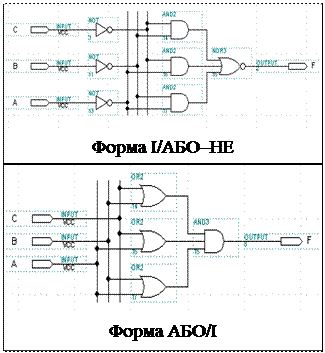 | 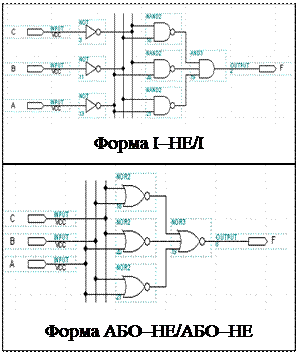 |
Рис. 12
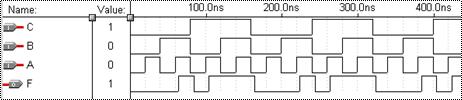
Рис. 14
