Производная, основные определения и понятия

В этой статье дадим основные понятия, на которых будет базироваться вся дальнейшая теория по теме производная функции одной переменной.

Путь x – аргумент функции f(x) и 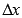- малое число, отличное от нуля.

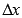(читается «дельта икс») называют приращением аргумента функции. На рисунке красной линией показано изменение аргумента от значения x до значения 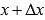(отсюда видна суть названия «приращение» аргумента).

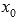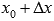При переходе от значения аргумента к значения функции изменяются соответственно от 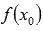до 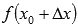при условии монотонности функции на отрезке 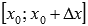. Разность называют приращением функции f(x), соответствующем данному приращению аргумента. На рисунке приращение функции показано синей линией.

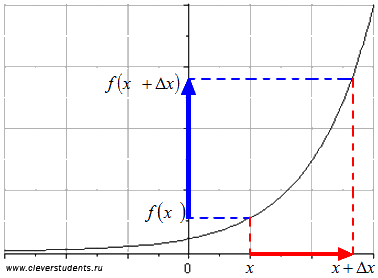
Рассмотрим эти понятия на конкретном примере.

Возьмем, к примеру, функцию 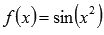. Зафиксируем точку 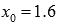и приращение аргумента 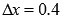. В этом случае приращение функции при переходе от 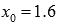к 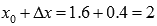будет равно

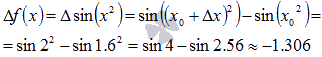
Отрицательное приращение 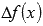говорит об убывании функции на отрезке .

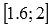Графическая иллюстрация

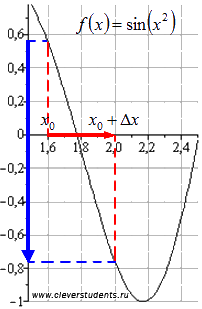
Определение производной функции в точке.

Пусть функция f(x) определена на промежутке (a; b), 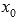и 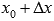- точки этого промежутка.Производной функции f(x) в точке 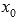называется предел отношения приращения функции к приращению аргумента при 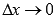. Обозначается .

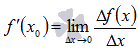Когда последний предел принимает конкретное конечное значение, то говорят о существовании конечной производной в точке. Если предел бесконечен, то говорят, чтопроизводная бесконечна в данной точке. Если же предел не существует, то и производная функции в этой точке не существует.

Функцию f(x) называют дифференцируемой в точке 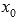, когда она имеет в ней конечную производную.

Если функция f(x) дифференцируема в каждой точке некоторого промежутка (a; b), то функцию называют дифференцируемой на этом промежутке. Таким образом, любой точке x из промежутка (a; b) можно поставить в соответствие значение производной функции в этой точке 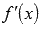, то есть, мы имеем возможность определить новую функцию 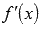, которую называют производной функции f(x) на интервале (a; b).

Операция нахождения производной называется дифференцированием.

Проведем разграничения в природе понятий производной функции в точке и на промежутке: производная функции в точке – это есть число, а производная функции на промежутке – это есть функция.

Давайте разберем это на примерах для ясности картины. При дифференцировании будем пользоваться определением производной, то есть переходить к нахождению пределов. При возникновении трудностей рекомендуем обращаться к разделу теории пределы, основные определения, примеры нахождения, задачи и подробные решения.

Производная. Рассмотрим некоторую функцию y = f ( x ) в двух точках x₀ и x₀ + 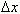: f ( x₀ ) и f ( x₀ + 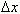). Здесь через 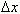обозначено некотороемалое изменение аргумента, называемое приращением аргумента; соответственно разность между двумя значениями функции: f ( x₀ + 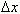) - f ( x₀)называется приращением функции. Производной функции y = f ( x ) в точке x₀называется предел:

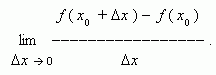
Если этот предел существует, то функция f ( x ) называется дифференцируемой в точке x₀ . Производная функции f ( x ) обозначается так:

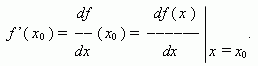
Геометрический смысл производной. Рассмотрим график функции y = f ( x ):

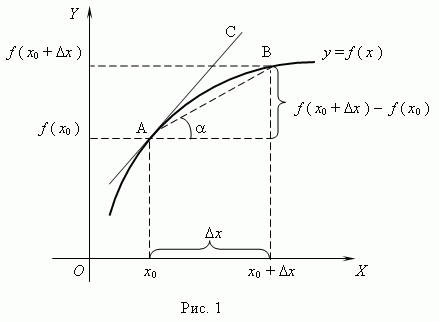
Из рис.1 видно, что для любых двух точек A и B графика функции:

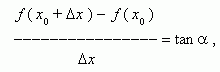
где 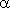- угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точкуB, то 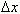неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует: производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.

Уравнение касательной. Выведем уравнение касательной к графику функции в точке A ( x₀ , f ( x₀) ). В общем случае уравнение прямой с угловым коэффициентом f ’( x₀) имеет вид:

y = f ’( x₀) · x + b .

Чтобы найти b,воспользуемся тем, что касательная проходит через точку A:

f ( x₀) = f ’( x₀) · x₀ + b ,

отсюда, b = f ( x₀) – f ’( x₀) · x₀, и подставляя это выражение вместо b, мы получим уравнение касательной:

y = f ( x₀) + f ’( x₀) · ( x – x₀) .

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x ( t ) времени t. В течение интервала времени от t₀ до t₀ + 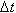точка перемещается на расстояние: x ( t₀ + 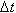) -x ( t₀ ) = 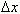, а её средняя скорость равна:v_a = 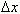/ 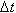. При 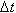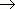0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v ( t₀) материальной точки в момент времени t₀ . Но по определению производной мы имеем:

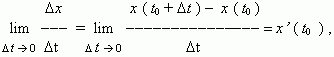
отсюда, v ( t₀) = x’ ( t₀) , т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной.Аналогично, ускорение – это производная скорости по времени: a = v’ ( t ).