Задача про максимальний потік у транспортній мережі
Транспортною мережею (s/t-мережі) назвемо зв`язний орієнтований граф без петель, у якого є дві особливі вершини s (джерело) та t (стік). Причому:
з вершини s дуги тільки виходять, а у вершину t – тільки заходять;
кожній дузі транспортної мережі приписана невід`ємна величина, яка називається пропускною спроможністю дуги і позначається cij.
Зафіксуємо деяку вершину s/t-мережі хк. Для поняття потоку транспортної мережі розглянемо дві множини А-множина всіх вершин s/t-мережі, з яких виходить дуга та заходить у вершину хк, та В – множина всіх вершин s/t-мережі, які безпосередньо слідують за вершиною хк. Тоді потоком в s/t-мережі будемо називати невід`ємну величину jij (для деякої дуги uij)=v, якщо виконуються наступні умови:
jij £ cij , для будь-якої дуги графа;
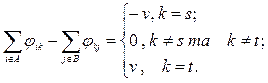
Перша умова говорить, що для будь-якої дуги транспортної мережі потік не перевищує пропускну спроможність транспортної мережі, а друга про те, що для будь –якої вершини транспортної мережі сумарний потік, що входить у вершину, рівний сумарному потоку, що виходить з вершини, тобто потік неподільний.
Нехай Х – множина всіх вершин s/t-мережі. Розіб`ємо її на дві підмножини Х1 та Х2 таким чином, щоб:
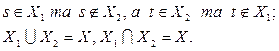
Тоді розтином s/t-мережі назвемо множину всіх дуг, що слідують з множини вершин Х1 до множини вершин Х2, позначимо (Х1, Х2). Величина розтину рівна сумі пропускних спроможностей дуг, що створюють розтин, та позначається v(X1, X2).
Задача про визначення максимального потоку в транспортній мережі є основною задачею оптимізації на графах. Її рішення базується на наступній теоремі Форда-Фалкерсона: максимальний потік у транспортній мережі дорівнює величині найменшого розтину в ній.
Задача 4. Транспортну мережу задано графічно. Необхідно знайти максимальний потік в s/t-мережі.
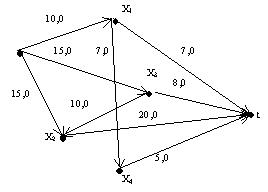
Розв`язок. Кожній дузі графа припишемо пару чисел cij, jij. На початку в s/t-мережі розподілимо нульовий потік, тобто jij=0. Далі для розмітки будь-якої к-ї вершини будемо використовувати позначення к(і+, e(к)) або к(і-, e(к)), де і- номер вершини, з якої ми потрапили до вершини к, ‘+’ - по прямій дузі, ‘-‘ - по зворотній дузі, e(к) – невід`ємна величина, на яку можна збільшити потік (для прямої дуги) або зменшити (для зворотної дуги). Вершина s завжди має особливу помітку (s+, ¥). Помічати вершини по прямих дугах можна, якщо на цих дугах потік можливо збільшити ( cij-jij >0), а по зворотніх – якщо потік можливо зменшити (jij >0). Для вершини к(і+, e(к)) e(к)=min(e(i), cik-jik), а для вершини к(і-, e(к)) e(к)=min(e(i), jik). Перший крок будь-якого етапу полягає у розставленні поміток вершин мережі, доки або не буде помічено вершину t , тоді переходимо на другий крок, або переконаємося, що вершину t помітити неможливо (задачу вирішено).
1-й єтап.
1-й крок. S(s+,¥). Далі помічаємо вершини суміжні з s. 1(s+, min(¥,10-0) , тобто 1(s+,10). Аналогічно 2(s+,15), 3(s+,15). Тепер вершина s розглянута. Для подальшого розгляду вибираємо будь-яку із суміжних помічених вершин. Наприклад, вершину 3. Помічаємо вершини, суміжні з третьою: 2(3+, min(15, 10-0)=10), t(3+, min(15,8-0)=8) Помітили вершину t – переходимо до друго кроку 1-го етапу.
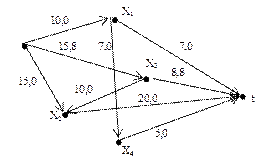
2-й крок. За допомогою поміток вершин будуємо ланцюг, який приводить з вершини s у вершину t: t3s. На прямих дугах ланцюга потік збільшуємо на величину e(t), а на зворотній – зменшуємо на цю саму величину. На малюнку показано розподіл потоку після виконання першого етапу. Переходимо до другого етапу, який виконуємо аналогічно першому.
2-й етап.
| S(s+,¥) | 1(s+,10) 2(s+,15) 3(s+,7) | t(2+,15) t2s e(t)=15 |
3-й етап.
| S(s+,¥) | 1(s+,10) 3(s+,7) | 4(1+,7) t(1+,7) t1s e(t)=7 |
Після 2-го та 3-го етапів розподіл потоку у мережі показано на малюнку.
4-й етап.
| S(s+,¥) | 1(s+,3) 3(s+,7) | 2(3+,7) | t(2+,5) t23s e(t)=5 |
5-й етап.
| S(s+,¥) | 1(s+,3) 3(s+,2) | 4(1+,3) | t(4+,3) t41s e(t)=3 |
6-й етап.
| S(s+,¥) | 3(s+,2) | 2(3+,2) | S(2-,2) |
На 1-му кроці 6-го етапу прийшли до побудови контуру навколо вершини s, а в вершину t так і не потрапили. Це свідчить про те, що потік у мережі збільшити неможливо. Будуємо розтин мережі: віднесемо до множини Х1 усі вершини, що помічені на 6-му кроці, а до множини Х2 – ті, що не помічені. Х1={s, 2, 3}, X2={1, 4, t}, (X1, X2)={us1, u2t, u3t}, v(X1, X2)=cs1+c2t+c3t=10+20+8=38. Перевірка: якщо просумувати всі значення e(t): 8+15+7+5+3=38, то отримаємо те саме значення величини розрізу.
Результуючій розподіл потоку в мережі має вигляд
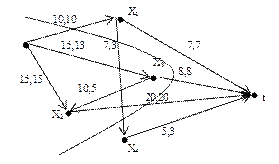 |
На малюнку також показано розріз найменшої величини, який побудовано у розглянутому прикладі.
Контрольна робота №3.
Завдання №1
Задано граф G. Представити граф у виді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, - методом Дейкстри, інші варіанти - методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом). Варіанти завдань знаходяться у додатку.
Завдання №2
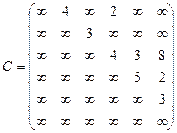
Орієнтований граф G=(X,U) заданий у видгляді матриці суміжності ваг С. Потрібно:
1) представити граф графічно й у видгляді матриці інциденцій;
2) визначити хроматичне число графа;
3) використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.
1. 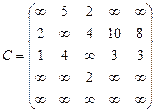 2.
2. 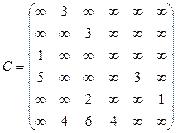
3. 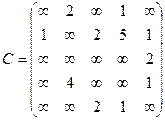 4.
4. 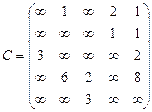
5. 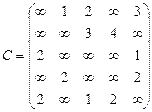 6.
6. 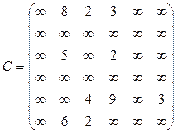
7. 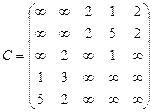 8.
8. 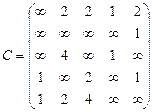
9.  10.
10. 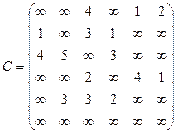
11. 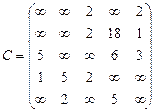 12.
12. 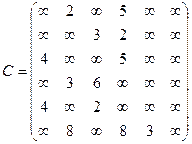
13. 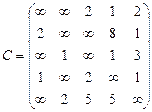 14.
14. 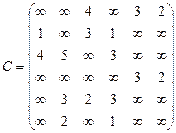
15. 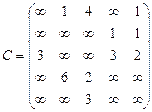 16.
16. 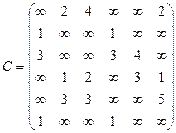
17. 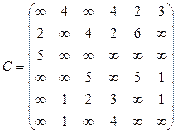 18.
18. 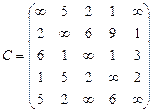
19. 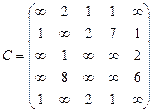 20.
20. 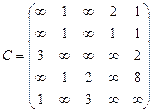
21. 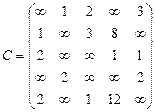 22.
22. 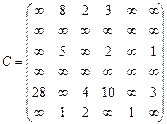
23. 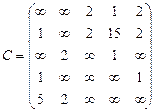 24.
24. 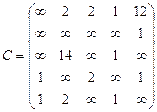
25. 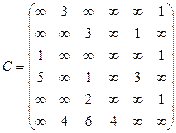 26.
26. 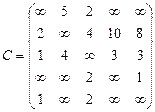
27. 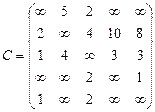 28.
28. 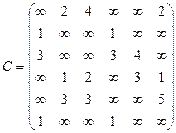
29.  30.
30. 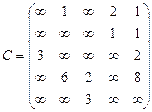
Завдання №3
У розподільній системі опрацювання даних у деякий момент часу є n ресурсів готових до виконання завдань. У систему надходить n завдань. Відома якість виконання завдань кожним ресурсом (коефіцієнти матриці С). Потрібно призначити кожному ресурсу своє завдання таким чином, щоб якість виконання всіх завдань була максимальною.
1. 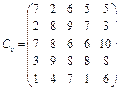 2.
2. 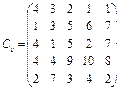
3. 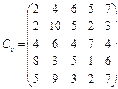 4.
4. 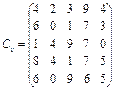
5. 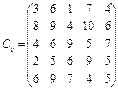 6.
6. 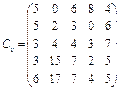
7. 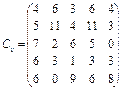 8.
8. 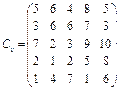
9. 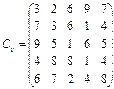 10.
10. 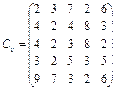
11. 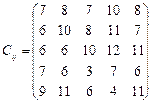 12.
12. 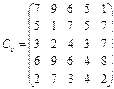
13. 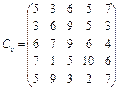 14.
14. 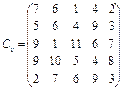
15. 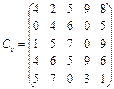 16.
16. 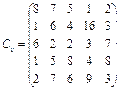
17. 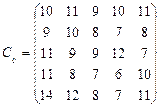 18.
18. 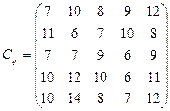
19. 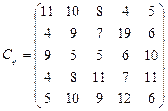 20.
20. 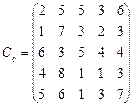
21. 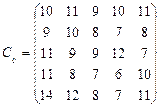 22.
22. 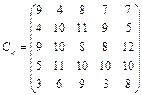
23. 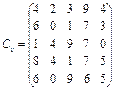 24.
24. 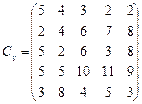
25. 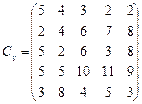 26.
26. 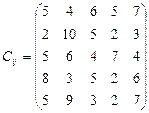
27. 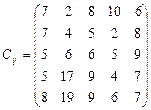 28.
28. 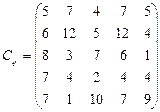
29. 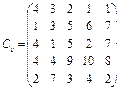 30.
30. 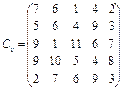
Завдання №4
Транспортна мережа задана за допомогою таблиці, де зазначені дуги мережі і пропускна спроможність цих дуг. Необхідно представити граф графічно і, використовуючи теорему Форда-Фалкерсона, визначити найбільший потік у мережі (s - джерело, t - стік). Перелік дуг мережі у вигляді 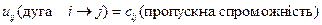
1. us1=13, us2=17, us3=1, u1t=7, u13=5, u23=2, u24=17, u34=1, u3t=2, u4t=12
2. us1=16, us2=14, u13=9, u21=10, u23=5, u24=8, u35=6, u3t=9, u45=1, u4t=6, u5t=6.
3. us1=6, us2=10, us3=3, u12=3, u14=2, u13=2, u24=1, u2t=8, u32=4, u34=5, u4t=9
4. us1=3, us2=5, us3=4, us4=1, u1t=7, u21=2, u24=1, u2t=1, u32=3, u34=2, u4t=3
5. us1=25, us2=18, u12=4, u14=10, u24=10, u2t=15, u3t=5, u43=10, u4t=10
6. us1=5, us2=4, us3=6, u1t=4, u14=1, u13=1, u23=3, u24=2, u34=2, u3t=3, u4t=7
7. us1=12, us2=20, us3=5, u1t=10, u13=8, u23=5, u24=10, u34=4, u3t=8, u4t=12
8. us1=8, us3=4, us4=6, u12=4, u24=2, u2t=10, u31=3, u32=2, u34=5, u4t=7
9. us1=10, us2=10, us3=15, u14=7, u12=4, u24=6, u32=5, u3t=20, u4t=10
10. us1=6, us2=7, us3=5, u12=3, u14=2, u13=1, u23=4, u24=2, u2t=3, u3t=7, u4t=8
11. us1=5, us2=6, us3=8, u12=2, u14=3, u13=1, u24=1, u2t=4, u3t=5, u4t=6
12. us1=10, us2=3, us3=15, u1t=5, u12=8, u23=16, u24=4, u2t=15, u34=5, u4t=20
13. us1=7, us4=15, ust=5, u1t=3, u13=5, u21=10, u34=3, u42=20, u4t=6
14. us1=20, us4=5, u12=17, u13=6, u24=10, u2t=3, u32=10, u3t=5, u4t=20
15. us1=25, us3=40, u14=20, u13=15, u2t=40, u32=20, u3t=15, u4t=7
16. us1=6, us2=14, u1t=10, u14=3, u23=3, u21=10, u24=2, u34=5, u4t=8
17. us1=5, us2=18, us5=7, u14=15, u23=25, u35=10, u3t=4, u43=10, u4t=10, u5t=2
18. us1=20, us2=10, us3=15, u12=15, u23=20, u25=15,u34=4,u35=8, u3t=1,u4t=20,u5t=4
19. us1=10, us2=5, us4=10, u12=1, u13=5, u14=8, u34=4, u3t=4, u42=5, u2t=20
20. us1=15, us2=20, us3=5, u1t=15, u12=8, u23=16, u24=4, u2t=10, u34=5, u4t=3
21. us1=10, us3=15, u14=8, u1t=13, u24=15, u31=6, u32=3, u3t=5, u4t=12
22. us3=10, us4=15, u1t=13, u2t=20, u31=8, u34=5, u41=2, u42=8, u4t=12
23. us1=15, us2=12, us3=11, u1t=9, u14=7, u13=6, u23=7, u21=10, u34=8, u3t=8, u4t=17
24. us1=13, us2=17, us3=1, u1t=7, u13=5, u23=2, u24=17, u34=1, u3t=2, u4t=12
25. us1=9, us2=7, us3=10, us4=12, u13=6, u14=8, u23=6, u24=6, u3t=14, u43=8, u4t=10
26. us1=8, us2=7, us4=16, u1t=7, u12=5, u23=10, u3t=12, u43=6, u45=10, u53=7, u5t=9
27. us1=11, us2=19, u1t=15, u14=8, u23=8, u21=15, u24=7, u34=10, u4t=13, u2t=2
28. us1=10, us2=3, us3=15, u1t=5, u12=8, u23=16, u24=4, u2t=15, u34=5, u4t=20
29. us1=5, us2=18, us5=7, u14=15, u23=25, u35=10, u3t=4, u43=10, u4t=10, u5t=2
30. us1=25, us2=18, u12=4, u14=10, u24=10, u2t=15, u3t=5, u43=10, u4t=10
31. us1=6, us2=10, us3=3, u12=3, u14=2, u13=2, u24=1, u2t=8, u32=4, u34=5, u4t=9
СПИСОК ЛІТЕРАТУРИ
1. Бардачов Ю.М., Соколова Н. А., Ходаков В.Є. Дискретна математика. – К. Вища школа , 2002. – 288 с.
2. Бондаренко М.Ф., Білоус Н.В., Руткас А.Г.Комп’ютерна дискретна математика. – Харків: Компанія СМІТ, 2004. – 480 с.
3. Капітонова Ю.В., Кривий С. Л., Летичевський о.А., Луцький Г.М., Печурін М. К. Основи дискретної математики: Підручник. – К.: ЛіфтСофт, 2000. –Т.2 – 380 с.
4. Новіков А.Ф. Дискретная математика. – СПб. Питер, 2004. – 302 с.
5. Тевяшев А.Д., Гусарова І.Г. Основи дискретної математики в прикладах і задачах.-Харків: ХНУРЕ, 2003.-272 с.
6. Андерсон Д.А. Дискретная математика и комбинаторика. – М. 2003, –960 с.
Методичні вказівки щодо практичних занять з навчальної дисципліни «Дискретна математика» до теми “теорія графів” для студентів денної форми навчання за напрямом 6.040302 – “Інформатика” (у тому числі скорочений термін навчання)
Укладачі к.т.н., доц. .А,І.Дерієнко
асист. І.І. Киба
Відповідальний за випуск: зав. кафедри інформатики та вищої математики проф. В.П. Ляшенко
Підп. до др. _________. Формат 60х84 1/16. Папір тип. Друк ризографія.
Ум. друк. арк. ____. Наклад _______ прим. Зам. №_______. Безкоштовно.
Видавничий відділ КрНУ
39614,м.Кременчук, вул. Першотравнева, 20
