Запишите решение заданий уровня В с полным обоснованием

В1.Найдите значение производной функции f(x)= в точке х₀=2007.

В2. Найдите максимум функции f(x)= .

В3. Напишите уравнение касательной к графику функции f(x)=х²+2х, параллельной прямой у=4х-5. В ответе укажите площадь треугольника, образованного этой касательной и осями координат.

Запишите решение заданий уровня С с полным обоснованием

С1. Рассматриваются всевозможные прямоугольные параллелепипеды, объем каждого из которых равен 32 см³, а одна из боковых граней является квадратом. Найдите среди них параллелепипед с наименьшим периметром основания. В ответе укажите этот периметр.

С2. При каких значениях b прямая у=bx является касательной к параболе

f(x)= х²-2х+4?

Диагностическая контрольная работа

По алгебре и началам анализа

«Производная функции. Приложения производной»

Вариант 4

Запишите вариант правильного ответа заданий уровня А

А1. На рисунке изображен график функции у=f(x). Укажите число промежутков возрастания функции.

а) 1 б) 2 в) 3 г) 0

А2. Укажите производную функции у= 2х³+ .

а) 2х2-

б) 6х2-

в) 6х2+

г) 6х-

А3. Найдите f '(4), если f(x)=4 -5.

а) 3 б) 2 в) -1 г) 1

А4. Найдите производную функции у=(х+3)sinx.

а) y'=(x+3)cosx б) y'=( +3x)cosx в) y'=cosx г) y'=sinx+(x+3)cosx

А5. Найдите точку максимума функции у=х³-3х+2.

а)-1 б) 0 в) 1 г) 4

А6.Укажите, какая из функций возрастает на всей координатной прямой.

а) у=х³+х б) у=х³-х в) у=-х³+х г) у= х²+1

А7. Найдите производную функции у=(4-3х)^5.

а) y'=20(4-3х)⁴ б) y'= 5(4-3х)⁴ в) y'= -15(4-3х)⁴ г) y'= -5(4-3х)⁴

А8.Укажите число точек экстремума функции у= 0,2х⁵- х³.

а) 0 б) 1 в) 2 г) 3

А9. Найдите угловой коэффициент касательной , проведенной к графику функции f(x)= 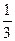х³-2х+7 в точке с абсциссой х₀=3.

а)7 б) 10 в) 0 г) -1

А10. Найдите момент остановки тела, движущегося по закону S(t)=t²-5t-14.

а) 7 б) -2 в) -2,5 г) 2,5

А11. Найдите наибольшее значение функции у=х³-3х на отрезке [-3;0].

а) -9 б) 4 в) 2 г) 9

А12. Найдите тангенс угла наклона касательной, проведенной к графику функции у = -0,5х² в его точке с абсциссой х₀= -3.

а) -3 б) -4,5 в) 3 г) 0