Неминимально-фазовые звенья
Звено называют минимально-фазовым, если все нули и полюса его передаточной функции имеют отрицательные или равные нулю вещественные части. Звено называют неминимально-фазовым, если хотя бы один нуль или полюс его передаточной функции имеет положительную вещественную часть.
Напомним, что нулями передаточной функции 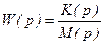 , где K(p) и M(p) - полиномы от p, называют корни уравнения K(p)=0, т.е. такие значения p, при которых передаточная функция обращается в нуль, а полюсами - корни уравнения M(p)=0, т.е. такие значения p, при которых передаточная функция обращается в бесконечность.
, где K(p) и M(p) - полиномы от p, называют корни уравнения K(p)=0, т.е. такие значения p, при которых передаточная функция обращается в нуль, а полюсами - корни уравнения M(p)=0, т.е. такие значения p, при которых передаточная функция обращается в бесконечность.
Все рассмотренные выше элементарные звенья являются минимально-фазовыми. В качестве примера неминимально-фазового звена рассмотрим инерционное звено первого порядка, уравнение динамики которого имеет вид:
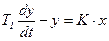 , (3.108)
, (3.108)
Переходя к изображению Лапласа, для передаточной функции получим выражение:
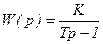 , (3.109)
, (3.109)
Частотная передаточная функция
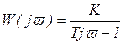 , (3.110)
, (3.110)
Разделяя на вещественную и мнимую части, получим:
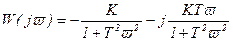 , (3.111)
, (3.111)
Из (3.111) видно, что данная АФЧХ отличается от АФЧХ минимально-фазового апериодического звена только знаком вещественной части, а амплитудно-частотные и логарифмические амплитудно-частотные характеристики полностью совпадают, так как
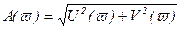 , (3.112)
, (3.112)
АФХ неминимально-фазового апериодического звена представлена на рисунке 3.11, а.
Фазочастотная характеристика
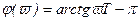 , (3.113)
, (3.113)
Из выражения (3.113) видно, что ФЧХ неминимально-фазового звена сдвинута по фазе относительно минимально-фазового звена на 180°, т.е. при изменении частоты от 0 до ¥ фаза изменяется от -p до -p/2. Графики логарифмических амплитудной и фазовой частотных характеристик представлены на рисунке 3.11, б.
Переходная характеристика
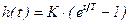 , (3.114)
, (3.114)
Весовая функция
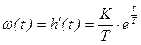 , (3.115)
, (3.115)
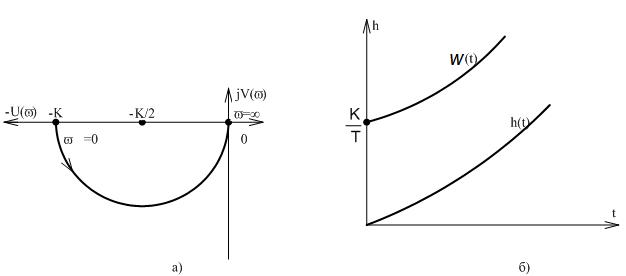
Рисунок 3.11 Характеристики неустойчивого апериодического звена
Из графиков на рисунке 3.11 видно, что при единичном воздействии переходная характеристика не имеет установившегося состояния, т.е. звено неустойчиво. Подобные звенья отличаются от типовых знаком любого члена передаточной функции W(p), например, для передаточных функций неминимально-фазовых звеньев можно записать выражения:
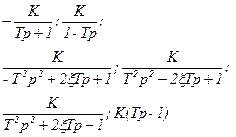 (3.116)
(3.116)
Звенья с запаздыванием
К неминимально-фазовым звеньям относят так же звено с чистым запаздыванием.
Звеном чистого запаздывания называют такое звено, выходная величина которого следует за входной с отставанием на время t, называемое постоянной запаздывания.
Наиболее распространенным в практике автоматических систем является транспортное запаздывание, обусловленное пространственным перемещением элементов, передающих информацию (например, транспортерная лента, полоса прокатываемого металла). Если рассматривать электромагнитное реле как динамическое звено, у которого входной величиной является напряжение, подводимое к катушке, а выходной напряжение коммутируемое контактами реле, то получим динамическое звено с чистым запаздыванием. Включение контактов реле, благодаря электромагнитной инерции катушки, запаздывает на некоторое время t по отношению к напряжению катушки, которое прикладывается в виде единичного скачка.
Уравнение звена постоянного запаздывания:
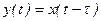 , (3.117)
, (3.117)
Передаточная функция звена:
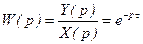 , (3.118)
, (3.118)
Частотная передаточная функция:
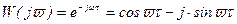 , (3.119)
, (3.119)
Модуль АФХ (рисунок 3.12, а) равен единице, а АФХ представляет собой окружность с центром в начале координат.
При возрастании v вектор W(jv) вращается по часовой стрелке, причем его конец обходит окружность бесконечное число раз.
Частоты в точках пересечения вещественной положительной полуоси
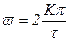 , (3.120)
, (3.120)
где K=0, 1, 2, 3...
Уравнения амплитудной и фазовой частотных характеристик:
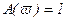 , (3.121)
, (3.121)
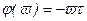 , (3.122)
, (3.122)
Так как A(v)=1, то ординаты ЛАХ равны нулю, т.е. ЛАХ совпадает с осью абсцисс. ЛФХ для абсолютного значения фазы представляет собой непрерывно-возрастающую кривую.
Переходная и импульсная функции:
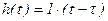 , (3.123)
, (3.123)
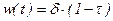 , (3.124)
, (3.124)
Частотные и временные характеристики звена с чистым запаздыванием показаны на (рисунок 3.12, б, в, г).
Звено с запаздыванием в некоторых случаях вводится при расчете системы условно. Для ряда промышленных объектов уравнение динамики неизвестно, поэтому кривую переходного процесса реального объекта при единичном входном воздействии аппроксимируют экспонентой и эквивалентным запаздыванием t.
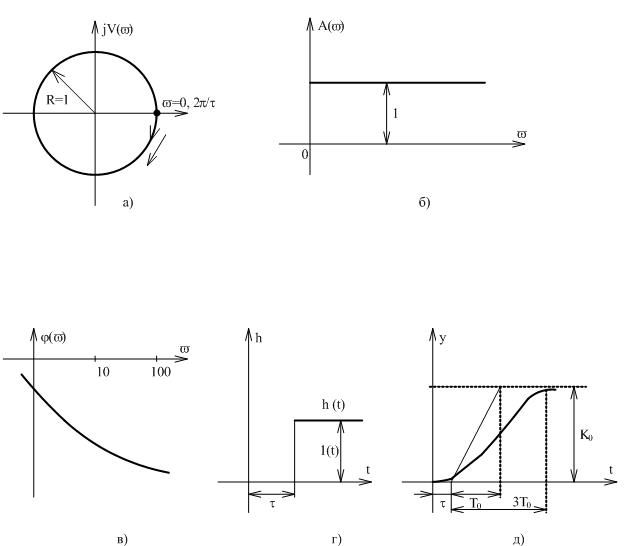
Рисунок 3.12 Характеристики звена с чистым запаздыванием
Время t определяется отрезком, который отсекается на оси абсцисс вспомогательной линией АВ, характеризующей постоянную времени Т0. При этом реальный объект аппроксимируется последовательным соединением звена с запаздыванием t и инерционного звена с коэффициентом усиления K0 и постоянной времени Т0:
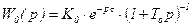 , (3.125)
, (3.125)
