Элементов в цепи гармонического тока

Комплексным сопротивлением участка цепи гармонического тока называется отношение комплексного напряжения на его концах к комплексному току этого участка цепи :

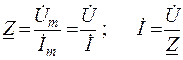. (2. 8)

Формулу (2. 8) можно называть выражением закона Ома в комплексной форме. В дальнейшем будем опускать индекс “m”, при необходимости оговаривая, о каком значении тока или напряжения идет речь. Используя комплексную форму записи напряжения и тока, выражение (2. 8) можно представить в следующем виде

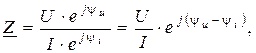
Величина 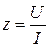, являющаяся модулем комплексного сопротивления, называется полным сопротивлением.

Величина 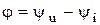представляет собой разность, или сдвиг фаз напряжения и тока. С учетом этих обозначений последнее выражение перепишем в виде

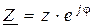. (2. 9)

Формула (2. 9) является показательной формой записи комплексного сопротивления. Применяя формулу Эйлера, его можно представить и так :

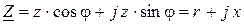. (2. 10)

Это алгебраическая форма записи комплексного сопротивления. Вещественная часть формулы (2. 10) 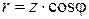называется активным сопротивлением, а мнимая часть 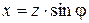- реактивным сопротивлением. Если известны rи x, то полное сопротивление определяется как 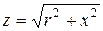, а угол сдвига фаз через соотношение .

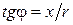Пример. Напряжение и ток на участке цепи изменяются по закону 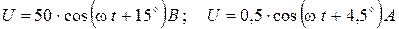. Определить комплексное сопротивление цепи.

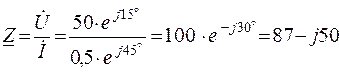Oм ;

z = 100 Ом; r = 87 Ом; x = -50 Ом.

Из этого примера видно, что реактивное сопротивление может быть отрицательным. Комплексное сопротивление цепи зависит от схемы цепи и типа элементов. Наиболее просто определять комплексное сопротивление и ток в цепи, состоящей из последовательно включенных элементов (рисунок 2. 5) .

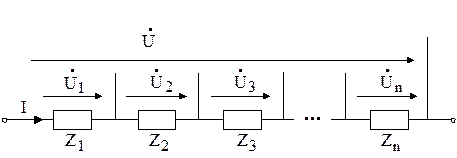
Рисунок 2.5

Как было показано, комплексное напряжение на зажимах цепи, состоящей из последовательно включенных элементов, равно сумме комплексных напряжений на отдельных элементах : 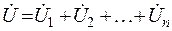. По определению (2. 8) напряжение на каждом элементе связано с током соотношением 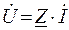. Поэтому 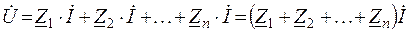; отсюда следует, что комплексное сопротивление последовательного соединения элементов равно сумме комплексных сопротивлений отдельных элементов

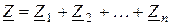. (2. 11)

Все случаи последовательного соединения исчерпываются последовательным соединением сопротивления, индуктивности и емкости. Поэтому достаточно найти комплексные сопротивления этих элементов и затем комплексное сопротивление их последовательного соединения. На основании закона Ома для идеального резистора

.

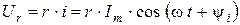Из этого выражения видно, что напряжение на резисторе по фазе совпадает с током. Переходя к комплексному изображению тока и напряжения, запишем 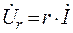. Таким образом, комплексное сопротивление идеального резистора равно r :

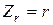. (2. 12)

Если через идеальную катушку индуктивности протекает гармонический ток 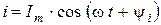, то согласно формуле (1. 5) , напряжение на ней будет также гармоническим :

.

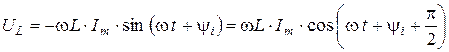Из этих выражений следует, что напряжение на индуктивности по фазе опережает ток на 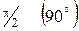. Величина 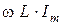имеет размерность напряжения, а произведение 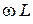- размерность сопротивления. Величина 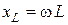называется индуктивным сопротивлением. Комплексная форма записи 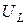имеет вид

.

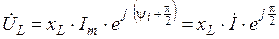Учитывая, что 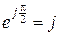, последнее выражение можно записать так

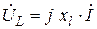. (2. 13)

Из формулы (2. 13) следует, что комплексное сопротивление индуктивности равно

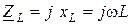. (2. 14)

Напряжение на идеальном конденсаторе при протекании через него гармонического тока найдем с помощью выражения (1. 4)

.

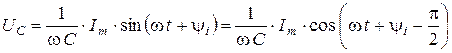Таким образом, напряжение на емкости отстает от тока по фазе на 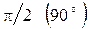. Величина 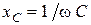имеет размерность сопротивления и называется емкостным сопротивлением.

Комплексное напряжение на емкости представляется выражением

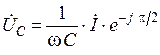или 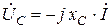. (2. 15)

Комплексное сопротивление емкости

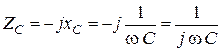. (2. 16)

Обратимся теперь к последовательному соединению сопротивления, индуктивности и емкости (рисунок 2. 6). Заметим что в этой схеме сопротивление r может быть не резистором, а активным сопротивлением катушки индуктивности.

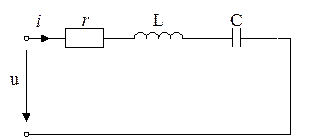
Рисунок 2. 6

Используя формулы (2. 11), (2. 12), (2. 14) и (2. 16), найдем комплексное сопротивление этой цепи

,

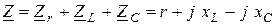или

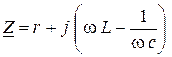. (2. 17)

Полное сопротивление цепи находим как модуль комплексного сопротивления

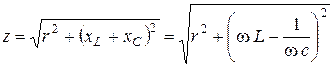, (2. 18)

а фазовый угол можно определить из соотношения

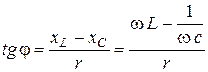. (2. 19)

С учетом (2. 17) и (2. 18) комплексное сопротивление цепи

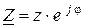. (2. 20)

Как показывает формула (2. 19), угол сдвига фаз может быть положительным 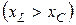, при этом ток отстает по фазе от положительного напряжения, и отрицательными 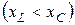, при этом ток опережает напряжение. Эти случаи иллюстрируются векторными диаграммами, приведенными на рисунке 2.7, а, б.

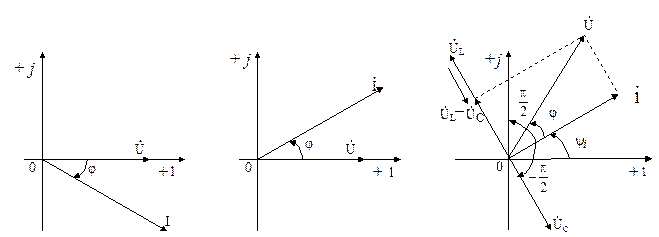
а) б) в)

Рисунок 2. 7

Реактивное сопротивление цепи равно 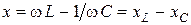и может быть положительным и отрицательным. Если цепь представляет собой последовательное соединение нескольких элементов R, C, L, то комплексное сопротивление находят суммированием отдельно активных и реактивных (с учетом знака) сопротивлений. Если в цепи (рис. 2. 6) задан ток 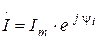, то напряжения на элементах цепи будут равны :

; ;

; ;

; .

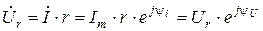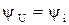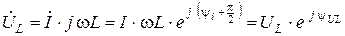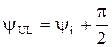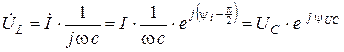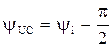Векторная диаграмма тока и напряжений приведена на рисунке 2. 7, в .

Пример. Найти комплексное сопротивление цепи, изображенной на

рисунке 2. 8 .

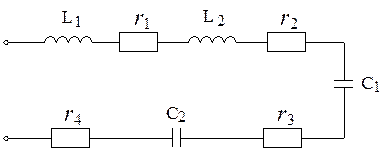
Рисунок 2. 8

Суммируя активные сопротивления, находим общее активное сопротивление : 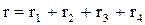и, суммируя с учетом знака реактивные сопротивления, - общее реактивное сопротивление :

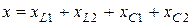или .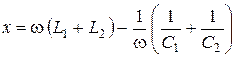

Из последнего равенства следует, что если в последовательной цепи имеется несколько индуктивностей и емкостей, то их можно заменить одной индуктивностью и одной емкостью, определяемыми из соотношений :

, .

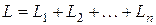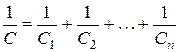Комплексное сопротивление определяется в соответствии с формулой (4. 17) .