Лемма о рукопожатии. Следствие

Теория графов. Понятие графа.

Графом называется набор точек (эти точки называются вершинами), некоторые из которых объявляются смежными (или соседними). Считается, что смежные вершины соединены между собой ребрами (или дугами).

Число вершин в графе — порядок, число рёбер — размер графа.

Граф называется ориентированным (или орграфом),если некоторые ребра имеют направление. Этоозначает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Геометрически граф часто изображают точками плоскости, причем соседние вершины соединены дугами (для орграфа некоторые дуги имеют направление, что обычно отмечают стрелкой).

способы задания графа

Явное задание графа как алгебраической системы.

Геометрический

Матрица смежности

Матрица инцидентности

Маршрут в графе – это последовательность соседних (смежных) вершин. Ясно, что можно определить маршрут и как последовательность смежных ребер (в этом случае ребра приобретаютнаправление). Заметим, что в маршруте могут повторяться вершины, но не ребра. Маршрут называется циклом, если в нем первая вершина совпадает с последней.

Путь в графе (иногда говорят простой путь) – это маршрут без повторения вершин (а значит, и ребер).

Контур – это цикл без повторения вершин, за исключением первой вершины, совпадающей с последней.

2. Основные понятия теории графов: понятие ребра, вершины, смежности вершин, инцидентности ребер, понятие петли.

Таким образом, ребро определяется парой вершин. Два ребра, у которых есть общая вершина, также называются смежными (или соседними).

Два ребра называются кратными, если множества их концевых вершин совпадают.

Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v, w, если оно соединяет эти вершины и наоборот, каждая из вершин v, w инцидентна ребру е.

Ребро называется петлёй, если его концы совпадают.

Понятие мультиграфа, псевдографа.

Псевдограф − граф, в котором есть петли и/или кратные ребра.

Мультиграф − псевдограф без петель.

Понятие степени вершины, порядка графа.

Степень вершины – это число ребер, входящих в эту вершину. Вершина называется висячей, если ее степень равна единице (0 - изолированная).

Число вершин графа называется его порядком и обозначается |G|.

Лемма о рукопожатии. Следствие.

Лемма: Сумма степеней всех вершин графа (или мультиграфа без петель) — четное число, равное удвоенному числу ребер.

Следствие 1 из леммы о рукопожатиях. Произвольный граф имеет четное число вершин нечетной степени.

Следствие 2 из леммы о рукопожатиях. Число ребер в полном графе n(n-1)/2.

6. Разновидности графов: полные графы, регулярные графы, простые графы, связные графы, полностью несвязные графы, Платоновы графы, двудольные графы

Граф G называется полным, если любые две его вершины смежны. Полный граф — простой граф, в котором каждая пара различных вершин смежна. Полный граф с 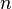вершинами имеет 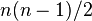рёбер и обозначается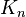

Регулярный граф — граф, степени всех вершин которого равны, то есть каждая вершина имеет одинаковое количество соседей.

Простой граф — граф, в котором нет кратныхрёбер и петель.

Связный граф — граф, в котором все вершины связаны.

У вполне несвязного графа все вершины изолированы.

Платоновы графы — графы, образованные вершинами и ребрами пяти правильных многогранников — платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.

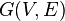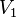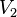Двудольный граф (или биграф, или чётный граф) — это граф , такой что множество вершин V разбито на два непересекающихся подмножества и , причём всякое ребро E инцидентно вершине из 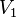и вершине из 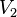(то есть соединяет вершину из 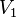с вершиной из 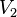). То есть, правильнаяраскраскаграфадвумя цветами. Множества 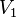и 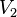называются «долями» двудольного графа. Двудольный граф называется «полным», если любые две вершины из 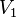и 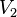являются смежными. Если 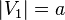, , 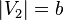то полный двудольный граф обозначается .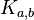