Звичайні Жорданові виключення
Нехай розглядається система
(і= 
). (1)
із m лінійних форм 
з n невідомими змінними 
Систему (1) можна записати у вигляді таблиці
= 
… 
… 
…………………..
= 
… 
… 
(2)
……………………
= 
… 
… 
Нехай потрібно виразити змінну х 
з r-го рівняння системи (1), а потім підставити одержану рівність у всі останні рівняння системи. Таке перетворення системи (1) називається кроком жорданового виключення з ключовим елементом а 
. Це перетворення добре виконувати, користуючись таблицею (2), яка потім переходи в таблицю (3) по наступному правилу:
1. 1. Ключовий елемент заміняється одиницею(над ключовим стовпчиком записується , а у ключовому рядочку х ).
2. 2. Решта елементів ключового стовпчика залишаються без змін.
3. 3. Решта елементів ключового рядочка міняють лише свої знаки.
4. 4. Елементи, що не належать ключовому рядочку чи стовпчику, обчислюються по формулі 
(i 
r, j s).
5. 5. Всі елементи нової таблиці діляться на ключовий елемент а , що в (3) зображено символічно діленням всієї таблиці на а :
(:а ) (3)
Наприклад, для таблиці 
один крок жорданових виключень з ключовими другим рядочком і третім стовпчиком, тобто міняються ролями змінні у 
і х приводять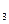 
, до таблиці
(:2). І кінцево до таблиці 
.
Для розв`язування системи з n лінійних рівнянь з n невідомими, визначник якої не рівний нулю, можна вказати різні варіанти застосування Жорданових виключень.
Метод Жордана-Гауса
Метод Жордана-Гауса реалізується наступним алгоритмом.
Алгоритм: Система 
Представимо її у вигляді таблиці
(1)
В таблиці вибираємо будь-який ключовий елемент, відмінний від нуля і не стоячий в стовпчику вільних членів( якщо можливо, то простіше в якості ключового елементу брати 1). Проводимо крок Жорданових виключень з вибраним ключовим елементом. В результаті одержуємо таблицю, в якій зліва буде деяке х 
, а зверху над стовпчиком-нуль. Викреслюємо цей стовпчик(тобто минулий стовпчик з ключовим елементом).
Повторюємо дію 2 до тих пір, поки не будуть переведені всі х вліво таблиці, тобто поки не прийдемо до таблиці 
,
із якої і одержуємо розв`язок х 
, х 
, ..., 
.
ПРИКЛАД1: Знайти розв`язок системи рівнянь методом Жордано-Гауса.
Розв`язання: Запишемо дану систему у вигляді 
.
Зробимо один крок Жорданових виключень з ключовим елементом а 
=1 і викреслюємо потім четвертий стовбець, що стоїть під нулем, одержимо таблицю 
.
Наступний крок зробимо з ключовим елементом, що стоїть у другому рядочку і третьому стовпчику. Після викреслювання третього стовпчика одержимо
.
Третій крок перетворень з ключовим елементом, що стоїть у четвертому рядочку і другому стовпчику, приводить до таблиці
, або 
.
Після четвертого кроку знайдемо остаточно 
.
Звідси х 
, х 
х 
х 
.
Зауваження: 1. Якщо визначник системи рівний нулю, (тобто система або несумісна, або має нескінчене число розв`язків, що виявляється в процесі розв`язання), то в результаті обчислення одержиться ситуація, коли деякі х залишаться зверху таблиці, а нулі - зліва і неможливо буде вибрати ключовий елемент, так як всі елементи в нуль стрічках нулі. Якщо при цьому і вільні члени цих стрічок (в стовпчику під 1) нулі, то система має нескінчене число розв`язків. В інакшому випадку система не має розв`язку.
Зауваження: 2. Описаний метод можна застосовувати і для розв`язування прямокутних систем (число рівнянь не рівне числу невідомих).
ПРИКЛАД 2: Розв`язати систему рівнянь методом Жордано-Гауса.
Розв`язання: Запишемо дану систему у вигляді
.
Виконаємо крок Жорданових виключень з ключовим елементом, що стоїть у першому рядочку і першому стовпчику, одержимо
.
Виконаємо крок Жорданових виключень з ключовим елементом, що стоїть у другому стовпчику і третьому рядочку, одержимо
.
Подальші обчислення неможливі, так як в залишеній нуль стрічці елементи під х і х 
нулі. Вільний член цієї стрічки не нуль, тому система несумісна: 0 -2.
6. Метод Гауса.Цей метод відрізняється від методу Жордано-Гауса лише тим, що після кожного кроку Жорданових виключень викреслюємо не тільки стовпчик з ключовим елементом, але і рядочок із ключовим елементом, але при цьому виписуємо окремо вираз для відповідного х .
Запишемо систему n рівнянь з невідомими у вигляді таблиці
Виберемо в якості ключового елемента будь-який елемент таблиці, відмінний від нуля і не стоїть в стовпчику вільних членів. Проведемо крок Жорданових виключень з ключовим елементом, після чого викреслюємо із таблиці стовпчик з ключовим елементом і виписуємо рядочок, що відповідає невідомому х . Повторяємо дію 2 до тих пір, поки не прийдемо до таблиці вигляду 
, тобто х 
.
Підставляємо послідовно з кінця до початку знайдені значення для х до тих пір, поки не одержимо значення всіх невідомих.
ПРИКЛАД: Розв`язати систему лінійних рівнянь методом Гауса
Розв`язання: Перепишемо систему у вигляді таблиці 
Вибираємо за ключовий елемент одиницю, що стоїть в першому рядочку і четвертому стовпчику. Проведемо крок Жорданових виключень. Викреслюємо четвертий стовпчик і виписуємо окремо першу стрічку, що представляє вираз для х . Будемо мати
,
і 
Вибираємо ключовий елемент одиницю, що стоїть в першому рядочку і третьому стовпчику. Проводимо крок Жорданових виключень і викреслюємо перший рядочок і третій стовпчик. Одержимо
, 
.
Проводимо крок Жорданових виключень з ключовим елементом -1, що стоїть у другому стовпчику і другому рядочку. Одержимо
, 
.
Знаходимо із останньої таблиці х 
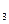=1. Підставимо його у вираз для х , одержимо х =-1+2=1, далі х =1-2=-1 і х =-2-2-1+4=-1.
Зауваження: 1. Якщо визначник системи рівний нулю, (тобто система або несумісна, або має нескінчене число розв`язків, що виявляється в процесі розв`язання), то в результаті обчислення одержиться ситуація, коли деякі х залишаться зверху таблиці, а нулі - зліва і неможливо буде вибрати ключовий елемент, так як всі елементи в нуль стрічках нулі. Якщо при цьому і вільні члени цих стрічок (в стовпчику під 1) нулі, то система має нескінчене число розв`язків. В інакшому випадку система не має розв`язку.
Зауваження: 2. Описаний метод можна застосовувати і для розв`язування прямокутних систем (число рівнянь не рівне числу невідомих).
Жорданові виключення можуть бути застосовані і для відшукання оберненої матриці. Нехай дана квадратна матриця
А= 
,
визначник якої не рівний нулю 
(А- не вироджена матриця). Представимо її у вигляді (1), позначивши через х (j=1, ...,n) стовпчики матриці, а через y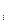 
(і=1,...,n) рядочки:
(1)
Проведемо над таблицею послідовно n кроків Жорданових виключень, перекинувши при цьому всі х вліво, а у 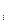вверх таблиці. Потім, якщо треба, переставимо рядки і стовпчики так, щоб х і у 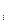розміщувались в порядку зростання їх номерів. Кінцева таблиця має вигляд
і матрицею цієї таблиці являється А 
, обернена матриця А.
ПРИКЛАД: Дана невироджена матриця А= 
.
Знайти матрицю А .
Розв`язання: Представимо матрицю у вигляді таблиці
Зробивши один крок Жорданових виключень з ключовим елементом, що знаходиться в першому рядку і першому стовпчику, одержимо таблицю
(:1)
Тепер зробимо ще один крок Жорданових виключень з кореневим елементом, що стоїть у другому стовпчику і у другому рядочку. Одержимо
(:-1)
і після ділення прийдемо до таблиці
.
Накінець, помінявши ролями х 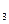і у 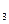, одержимо таблицю
(:8).
В кінцевому рахунку 
На цьому обчислення закінчується і оберненою буде матриця, записана в останній таблиці. Зазвичай в таблиці, отриманій після виконання всіх кроків Жорданових виключень, приходиться ще переставляти деякі рядки і стовпчики, якщо серед ключових елементів не всі були діагональними.
Зауваження: Якщо матриця А вироджена, тобто 
=0, то це виявиться в процесі розв`язку. Певні y 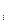не вдається перекинути вверх таблиці (або х вліво таблиці). Така ситуація виникає, якщо на перетині рядка y 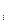і всіх стовпчиків, зверху яких х , стануть нулі. Максимальне число y 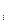, перекинутих вверх таблиці (або х - вліво таблиці), буде рівне рангу матриці А.
МЕТОД ОБЕРНЕНОЇ МАТРИЦІ
Жорданові виключення дозволяють відшукати розв`язок системи n рівнянь з n невідомими третім способом – методом оберненої матриці. Для цього запишемо систему у вигляді 
.
Проробивши послідовно n кроків Жорданових виключень, після можливих перестановок стрічок і стовпчиків, одержимо
, або 
.
Звідси 