Граничний перехід у нерівностях

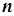Теорема . Якщо елементи збіжної послідовності , починаючи з деякого номера , задовольняють нерівність 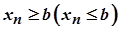, то і границя цієї послідовності задовольняє нерівність .

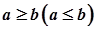Доведення. Нехай, починаючи з деякого номера 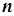, елементи збіжної послідовності задовольняють нерівність і 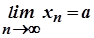. Припустимо, що 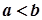. Оскільки 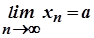, то для 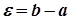існує номер 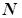такий, що для 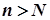виконується нерівність 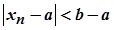, яка рівносильна нерівності 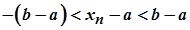. Тоді із нерівності одержуємо: , що суперечить умові. Отже, .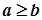

Випадок 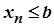доводиться аналогічно.

Наслідок 1. Якщо елементи збіжних послідовностей і 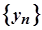, починаючи з деякого номера 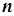, задовольняють нерівність , то .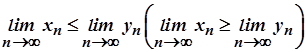

Нехай, починаючи з деякого номера, виконується нерівність 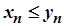. Тоді для таких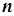 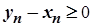. Отже, 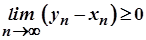, а тому 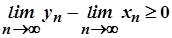. Звідси маємо 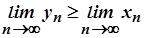. Другий випадок установлюється аналогічно.

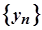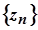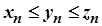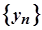Теорема. Нехай члени послідовностей , , , починаючи з деякого номера, задовольняють нерівність і . Тоді послідовність збіжна й .

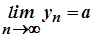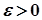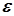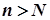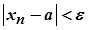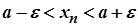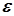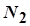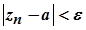Доведення. Задамо довільне число . Тоді для заданого знайдеться такий номер , що для виконуватиметься нерівність , тобто . Для цього ж знайдеться такий номер , що для 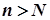, тобто .

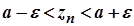Виберемо 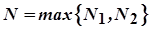. Тоді виконуватиметься нерівність

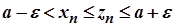
для всіх .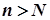

Ураховуючи умову теореми, маємо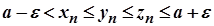

або 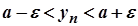, тобто 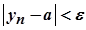для всіх 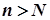. Звідси випливає, що .

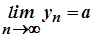Монотонні послідовності

Послідовність називається неспадною ( незростаючою ), якщо виконується нерівність 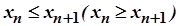для усіх .

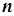Неспадні та незростаючі послідовності називаються монотонними.

Якщо для всіх членів монотонної послідовності виконується строга нерівність 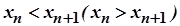, то послідовність називається зростаючою (спадною). Зростаючі та спадні послідовності називаються також строго монотонними.

З означення випливає, що монотонні послідовності обмежені принаймні з однієї сторони: неспадна обмежена знизу, а незростаюча – зверху.

Теорема. Монотонна обмежена послідовність збіжна.

Доведення. Розглянемо випадок неспадної послідовності .

Отже, нехай для усіх 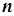виконуються наступні умови:

1) ;

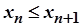2) існує таке числ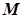о , що .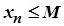

Розглянемо числову множину 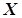, яка складається з усіх елементів послідовності . За умовою ця множина непорожня і обмежена зверху, а тому має точну верхню межу.

Позначимо 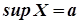. Покажемо, що .

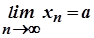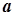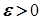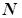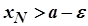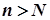Оскільки - точна верхня межа елементів послідовності , то, згідно з властивістю точної верхньої межі, для будь-якого існує номер такий, що . Так як послідовність неспадна, то при виконується нерівність 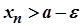. З іншого боку, згідно з означенням точної верхньої межі, 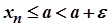для всіх 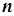. Таким чином, при 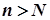маємо нерівність 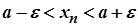, тобто 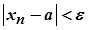при 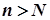. Отже, .

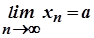Для випадку незростаючої послідовності доведення аналогічне.

*** Із теорем 2.5** і 2.8** випливає, що обмеженість монотонної послідовності є необхідною і достатньою умовою її збіжності.

Число е

Розглянемо послідовність з загальним членом 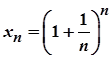. Покажемо, що ця послідовність є збіжною. Для цього спочатку установимо, що вона зростаюча, а потім – що вона обмежена.

Згідно формули бінома Ньютона

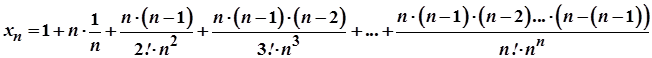
Подамо цей вираз у наступному вигляді

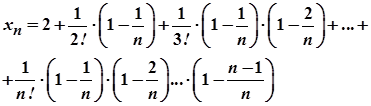(3)

Так само одержуємо

.

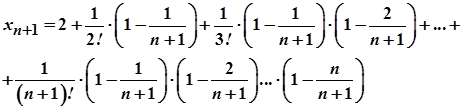При 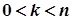виконується нерівність , тому 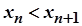, тобто послідовність зростаюча.

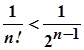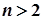Оскільки кожний вираз, який стоїть у дужках у формулі (3) менший від одиниці і при , то

.

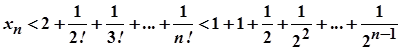За формулою суми нескінченно спадної геометричної прогресії маємо

.

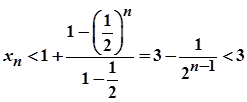Отже, послідовність обмежена. Таким чином, послідовність із загальним членом 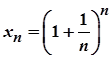збіжна. За означенням границю цієї послідовності позначають буквою 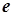, тобто

.