Марковские случайные процессы с дискретными состояниями и дискретным временем

Определение. Случайный процесс, протекающий в системе S с дискретными состояниями s₁, s₂, …, s_i, …, называется марковским, если для любого момента времени t₀ вероятность каждого из состояний системы в будущем (при t > t₀), зависит только от ее состояния в настоящем (при t = t₀), и не зависит от того, как система пришла в это состояние, т.е. не зависит от ее поведения в прошлом (при t < t₀).

Примеры. 1) Система S – счетчик в такси. Состояние системы в момент t характеризуется количеством километров, пройденных автомобилем до данного момента. Пусть в момент t₀ счетчик показывает S₀. Вероятность того, что в момент t > t₀ счетчик покажет то или иное количество километров (точнее, соответствующее количество денег) S₁, зависит только от S₀, но не зависит от того, в какие моменты времени изменялись показания счетчика до момента t₀.

2) Многие процессы можно приближенно считать марковскими. Например, процесс игры в шахматы. Система S – группа шахматных фигур. Состояние системы характеризуется числом фигур противника, сохранившимися на доске в момент t₀. Вероятность того, что в момент t > t₀ перевес будет на стороне одного из игроков, зависит в первую очередь от того, в каком состоянии система находится в данный момент t₀, а не от того, когда и в какой последовательности исчезли фигуры с доски до момента t₀.

В ряде случаев предысторией рассматриваемых процессов можно просто пренебречь и применить для их изучения марковские модели.

Пусть имеется система S с дискретными состояниями s₁, s₂, …, s_n (для простоты ограничимся конечным числом состояний). Предположим, что случайные переходы системы из состояния в состояние могут происходить только в определенные моменты времени t₀, t₁, t₃…. Сам процесс представляет собой случайное блуждание системы S по состояниям: после первого шага система может оказаться в одном (и только одном) из своих возможных состояний s₁⁽¹⁾, s₂⁽¹⁾, …, s_n⁽¹⁾, на втором шаге - s₁⁽²⁾, s₂⁽²⁾, …, s_n⁽²⁾, и т.д.

Определение. Марковским случайным процессом с дискретными состояниями и дискретным временем или цепью Маркова называется марковский процесс, в котором его возможные состояния можно заранее перечислить, а переход из состояния в состояние происходит мгновенно (скачком), но только в определенные моменты времени t0, t1, t2, …, называемые шагами процесса.

Из определения цепи Маркова следует, что для нее вероятности перехода системы S в состояние s_j на (k+1)–м шаге зависит только от того, в каком состоянии s_i находилась система на предыдущем, k–м шаге, и не зависит от того, как она вела себя до этого. Основной задачей исследования цепей Маркова является нахождение безусловных вероятностей нахождения системы S на любом (k–м) шаге в состоянии s_i; обозначим эту вероятность p_i(k):

p_i(k) = P{S(k) = s_i}, i = 1,2,…,n; k = 0,1,…

Для нахождения этих вероятностей необходимо знать условные вероятности перехода системы S в состояние s_j на k–м шаге, если известно, что на предыдущем (k-1)–м шаге на была в состоянии s_i. Обозначим эту вероятность

p_ij(k) = P{S(k) = s_j | S(k-1) = s_i }, i,j = 1,2,…,n.

Вероятности p_ij(k) называются переходными вероятностями марковской цепи на k–м шаге. Вероятность p_ii(k) есть вероятность того, что на k–м шаге система задержится (останется) в состоянии s_i.

Если переходные вероятности p_ij(k) не зависят от номера шага процесса k: p_ij(k) = p_ij, то такая цепь Маркова называется однородной.

Переходные вероятности можно записать в виде квадратной матрицы размерности nxn:

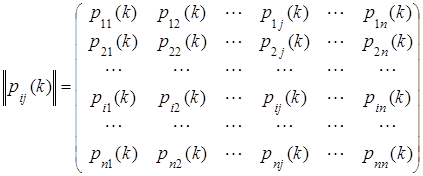(k = 0,1,2,…) (1)

На главной диагонали матрицы переходных состояний стоят вероятности задержки системы в данном состоянии s_j на k–м шаге - p₁₁(k), p₂₂(k),…, p_nn(k).

Так как на каждом шаге система S может находиться только в одном из взаимно исключающих состояний, то для любой строки матрицы переходных состояний сумма всех стоящих в ней вероятностей p_ij(k) равна единице:

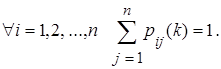(2)

Естественно, все элементы такой матрицы отвечают условию 0 ≤ p_ij(k) ≤ 1.

В силу условия (2) можно в матрице (1) не задавать вероятности задержки, а получать их как дополнения до единицы суммы всех остальных членов строки:

p_ii(k) =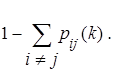

Для того, чтобы найти безусловные вероятности p_i(k), недостаточно знать матрицу переходных вероятностей (1); нужно еще знать начальное распределение вероятностей, т.е. вероятности состояний p_i(0), соответствующее началу процесса - моменту времени t₀ = 0: p₁(0), p₂(0), …, p_n(0), в сумме образующие единицу

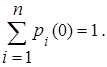
При выводе формул для вероятностей состояний мы в целях простоты записи будем рассматривать только однородные цепи Маркова, для которых матрица переходных вероятностей имеет вид

.

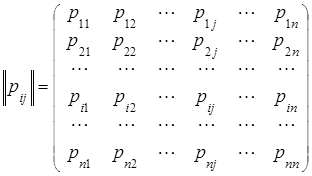При нахождении вероятностей состояний марковской цепи на k-том шаге p_i(k) (k = 1,2,…) удобно бывает пользоваться так называемым размеченным графом системы S, где возле каждой стрелки, ведущей из состояния s_i в состояние s_j, проставлена переходная вероятность p_ij; вероятности задержки на размеченном графе не проставляются, а просто получаются дополнением до единицы суммы вероятностей, стоящих у всех стрелок, ведущих из данного состояния s_i.

Пусть размеченный граф состояний выглядит следующим образом.

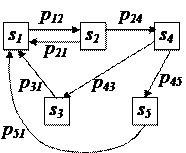Для этого графа вероятности задержек равны:

р₁₁ = 1 – р₁₂, р₂₂ = 1 – (р₁₂ + р₂₄), р₃₃ = 1 – р₃₁, р₄₄ = 1 – (р₄₃ + р₄₅), р₅₅ = 1 – р₅₁.

Если состояние s_i является поглощающим (на графе из него не идет ни одной стрелки), то вероятность задержки в этом состоянии равна 1.

Теперь покажем, как найти для однородной цепи Маркова безусловную вероятность нахождения системы S на k-том шаге в состоянии s_j (j = 1,2,…,n): p_i(k) = P{S(k) = s_j}, если задана матрица переходных вероятностей и начальное распределение вероятностей.

Пусть задана однородная цепь Маркова, имеющая матрицу переходных состояний 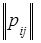и начальное распределение вероятностей p_i(0) (i = 1,2,…,n), 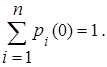Сделаем гипотезу, состоящую в том, что в начальный момент (k=0) система находилась в состоянии s_i. Вероятность этой гипотезы известна из начальных условий и равна p_i(0) = P{S(0) = s_i}. В предположении, что эта гипотеза имеет место, условная вероятность того, что система S на первом шаге будет в состоянии s_j, равна переходной вероятности p_ij = P{S(1) = s_j | S(0) = s_i}.

По формуле полной вероятности получим

p_j(1) = 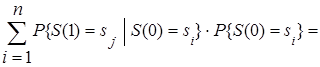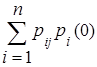(j = 1,2,…,n).

Таким образом, мы нашли распределение вероятностей системы S на первом шаге. Теперь у нас есть все необходимое, чтобы найти распределение вероятностей на втором шаге, которое для цепи Маркова зависит только от распределения вероятностей на первом шаге и матрицы переходных вероятностей.

Опять сделаем гипотезу, состоящую в том, что на первом шаге система находится в состоянии s_i; вероятность этой гипотезы нам уже известна и равна p_j(1) = P{S(1) = s_i}(i = 1,2,…,n). При этой гипотезе условная вероятность того, что система S на втором шаге будет в состоянии s_j, равна

p_ij = P{S(2) = s_j | S(1) = s_i}.

По формуле полной вероятности находим

p_j(2) = 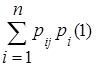(j = 1,2,…,n).

Переходя таким образом от k = 2 к k = 3 и т.д., получим рекуррентную (т.е. выражающую каждый член последовательности через предыдущие члены этой последовательности) формулу

p_j(k) = 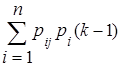(k = 1,2,…; j = 1,2,…,n).

Эта формула называется равенством Маркова.

Убедимся в том, что, зная все вероятности перехода р_ij = р_ij(1), т.е. матрицу перехода Р₁ из состояния в состояние за один шаг, можно найти вероятность р_ij(2), т.е. матрицу Р₂ перехода из состояния в состояние за два шага. А зная матрицу Р₂ – найти матрицу Р₃ перехода из состояния в состояние за 3 шага и т.д.

Действительно, полагая в равенстве Маркова k = 2

р_j(2) = = .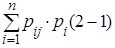

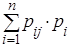Полученное равенство означает, что Р₂ = Р₁ ∙ Р₁ = .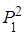

Полагая k = 3, аналогично получаем Р₃ = Р₁ ∙ Р₂ = Р₁ ∙ 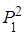= 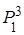, а в общем случае

Р_n = .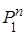

Теперь сформулируем теорему, позволяющую вычислить вероятности состояний системы от любого k-го до (k+1)-го шага, зная начальное распределение вероятностей p₁(0), …, p_n(0) и матрицу переходных вероятностей.

Теорема. Для однородной марковской цепи вектор-строка вероятностей состояний от k-го до (k+1)-го шага равна произведению вектор-строки вероятностей состояний от (k-1)-го до k-го шага на матрицу переходных вероятностей:

(p₁(k), …, p_n(k)) = (p₁(k-1), …, p_n(k-1))∙Р.

Следствие. Для однородной марковской цепи имеет место следующая формула

(p₁(k), …, p_n(k)) = (p₁(0), …, p_n(0))∙Рⁿ.

Замечание. Если марковская цепь является неоднородной, т.е. переходные вероятности (хотя бы одна) зависят от номера шага k, то приведенная формула вычисления вероятностей состояний системы приобретает следующий вид:

(p₁(k), …, p_n(k)) = (p₁(0), …, p_n(0))∙Р(1)∙…∙P(k),

где P(k) – матрица переходных вероятностей от k-го до (k+1)-го шага.