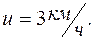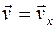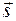Скорость материальной точки при равнопеременном движении
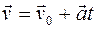 . (1.25)
. (1.25)
С учетом уравнения (1.25) перемещение  при равнопеременном движении может быть найдено по следующими формулам:
при равнопеременном движении может быть найдено по следующими формулам:
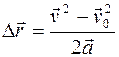 , (1.26)
, (1.26)
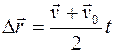 . (1.27)
. (1.27)
Вопросы для самоподготовки
1. Дайте определение вектора, его длины.
2. Расскажите обо всех возможных действиях с векторами.
3. Назовите физические модели в механике, дайте им определения.
4. Назовите виды механического движения.
5. Сформулируйте определение радиус-вектора.
6. Дайте определение прямолинейного равномерного и прямолинейного равнопеременного движения.
7. Сформулируйте понятие средней путевой скорости.
8. Назовите средние и мгновенные характеристики поступательного движения, дайте им определения.
9. Дайте определение пути, пройденного материальной точкой за некоторый промежуток времени.
10. Объясните, как найти ускорение при криволинейном движении?
11. Проанализируйте, как движется материальная точка в следующих случаях:
а) тангенциальное ускорение аτ>0, нормальное ускорение  =0;
=0;
б) аτ<0,  =0;
=0;
в) аτ=0,  >0;
>0;
г) аτ<0,  >0;
>0;
д) аτ>0,  >0.
>0.
12. Выведите кинематические уравнения равномерного и равнопеременного движения.
13. Выведите уравнение скорости материальной точки при равнопеременном движении.
Примеры решения задач
1.1.Радиус-вектор точки А относительно начала координат меняется со временем t по закону 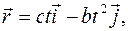 где c и b – положительные постоянные,
где c и b – положительные постоянные, 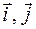 - орты осей OX и OY. Найти:
- орты осей OX и OY. Найти:
1) уравнение траектории точки у(х);
2) зависимость от времени векторов скорости  , ускорения
, ускорения  и модулей этих величин;
и модулей этих величин;
3) зависимость от времени угла 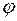 между векторами
между векторами  и
и  ;
;
4) средний вектор скорости за первые t секунд движения и модуль этого вектора.
Дано: Найти:
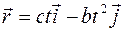 . 1. y(x);
. 1. y(x);
2. 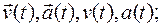
3. 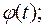
4. 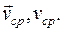
Решение:
1. В данной задаче рассматривается движение точки А, положение которой в пространстве задается радиус-вектором 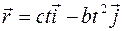 . В соответствии с формулой 1.9 можно получить:
. В соответствии с формулой 1.9 можно получить:
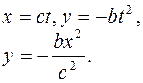 (1)
(1)
Движение материальной точки происходит в плоскости XOY, так как координата z=0.
2. Зависимость от времени вектора мгновенной скорости можно найти по формуле (1.13):
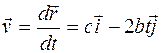 , (2)
, (2)
где 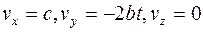 (3)
(3)
- проекции вектора скорости на оси координат ОХ, ОY, OZ. С учетом выражения (3), по формуле (1.15) можно найти модуль вектора скорости:
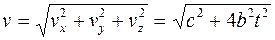 . (4)
. (4)
Вектор ускорения можно найти по формуле (1.16), используя выражение (2):
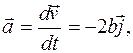 где
где 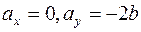 (5)
(5)
- проекции вектора ускорения на оси координат. Модуль вектора ускорения можно найти по формуле (1.17), используя выражение (5):
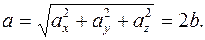
 (6)
(6)
3. Зависимость от времени угла 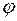 между
между  и
и  можно найти из следующих рассуждений.
можно найти из следующих рассуждений.
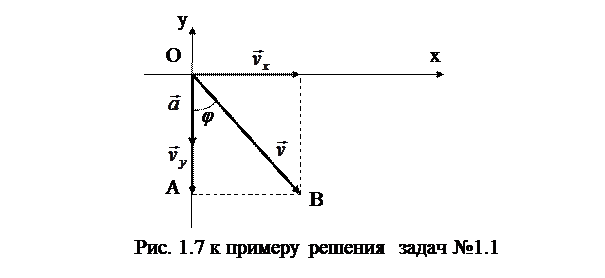
Вектор  направлен вдоль оси ОY, сонаправлен с вектором
направлен вдоль оси ОY, сонаправлен с вектором 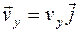 , не меняет своей величины и направления, так как не зависит от времени (
, не меняет своей величины и направления, так как не зависит от времени ( 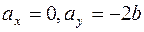 ). Вектор
). Вектор  меняет свою величину и направление с ростом компоненты
меняет свою величину и направление с ростом компоненты 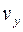 (
( 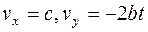 ). Поэтому зависимость угла
). Поэтому зависимость угла 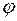 от времени можно найти из соотношения в треугольнике ОАВ (рис.1.7):
от времени можно найти из соотношения в треугольнике ОАВ (рис.1.7):
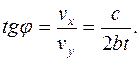 (7)
(7)
4. Исходя из того, что вектор перемещения 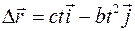 , по формуле (1.11) можно найти средний вектор скорости за первые
, по формуле (1.11) можно найти средний вектор скорости за первые  секунд движения:
секунд движения:
 , где
, где 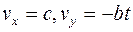 (8)
(8)
- проекции среднего вектора скорости на оси ОХ и ОY. Для нахождения модуля среднего вектора скорости можно воспользоваться формулой (1.15) и выражением (10):
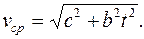
Ответ: 1. 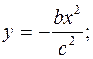 2.
2. 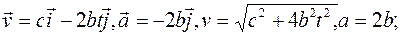
3.  4.
4. 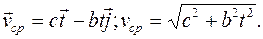
1.2.Два тела бросили одновременно из одной точки: одно – вертикально вверх, другое – под углом 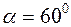 к горизонту. Начальная скорость каждого тела
к горизонту. Начальная скорость каждого тела 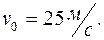 Пренебрегая сопротивлением воздуха, найти расстояние между телами через
Пренебрегая сопротивлением воздуха, найти расстояние между телами через 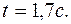
Дано: Найти:
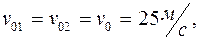
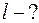
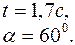
Решение:
Введем декартову систему координат, начало отсчета (точку О) которой совместим с точкой, из которой были брошены оба тела. Первое тело движется равнозамедленно вдоль оси ОY и в момент времени  находится в точке А (рис.1.8) с координатами:
находится в точке А (рис.1.8) с координатами:
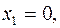
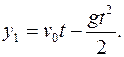
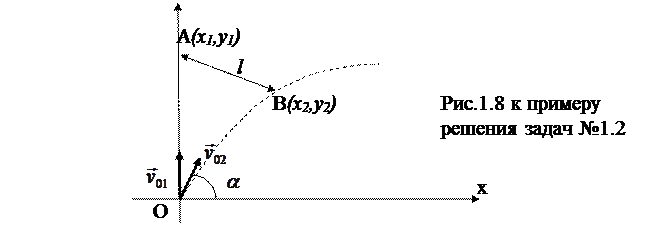
Движение второго тела можно представить как наложение двух видов движений: а) равнопеременного с ускорением свободного падения  вдоль оси OY, б) равномерного с постоянной скоростью
вдоль оси OY, б) равномерного с постоянной скоростью 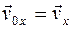 вдоль оси OX.
вдоль оси OX.
Таким образом, в момент времени  второе тело находится в точке В (рис.1.8) с координатами:
второе тело находится в точке В (рис.1.8) с координатами:
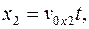
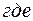
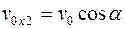 , тогда
, тогда
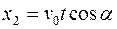 ;
;
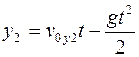 ,
, 
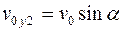 , то
, то
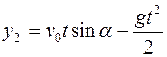 .
.
Расстояние между точкой А( 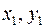 ) и точкой В(
) и точкой В( 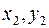 ) можно определить по формуле (1.2):
) можно определить по формуле (1.2):
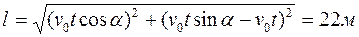 .
.
Ответ: l=22м.
1.3.Под каким углом к горизонту надо бросить шарик, чтобы:
1) центр кривизны вершины траектории находился на земной поверхности?
2) радиус кривизны начала его траектории был в n=8 раз больше, чем в вершине;
Дано: Найти:
1) R=hφ-?
2) R1=nR2, n=8
Решение:
1. Движение тела, брошенного под углом к горизонту, можно представить как наложение двух видов движений:
а) равномерного, с постоянной скоростью 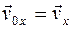 , вдоль оси OX;
, вдоль оси OX;
б) равнопеременного, с ускорением свободного падения  , вдоль оси OY.
, вдоль оси OY.
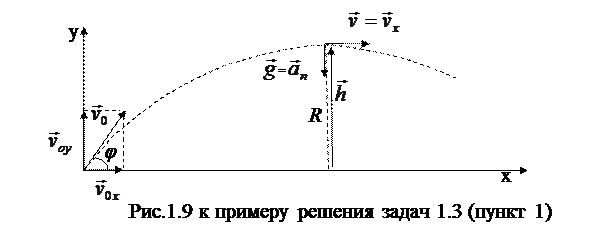
Тогда максимальная высота подъема по оси OY может быть найдена по формуле (1.26):
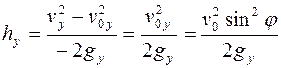 , (1)
, (1)
где 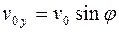 ,
, 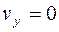 - проекция вектора скорости
- проекция вектора скорости  в вершине траектории на ось OY (рис.1.9), gy – проекция вектора
в вершине траектории на ось OY (рис.1.9), gy – проекция вектора  на ось OY.
на ось OY.
Из условия задачи известно, что центр кривизны вершины траектории находится на земной поверхности, следовательно, максимальная высота подъема h=hy равна радиусу кривизны R вершины траектории и может быть найдена по формуле (1.19):
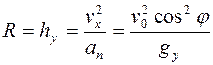 , (2)
, (2)
где 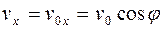 , an=gy (рис. 1.9).
, an=gy (рис. 1.9).
Совместное решение уравнений (1) и (2) дает искомую величину:
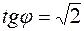 или φ=54,70.
или φ=54,70.
2. Угол φ можно найти из соотношения в прямоугольном треугольнике (рис. 1.10):
cosφ= 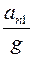 . (3)
. (3)
Нормальное ускорение в начальной точке траектории можно найти по формуле (1.19):
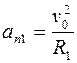 . (4)
. (4)
|
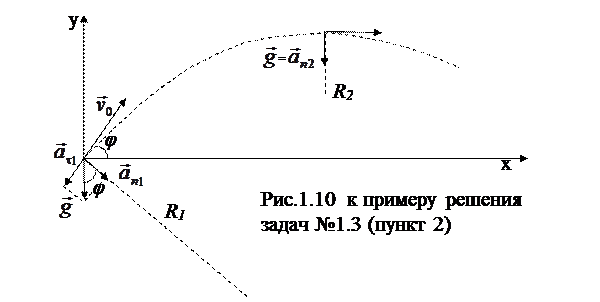
С учетом следующих очевидных соотношений: 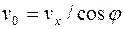 , R1=nR2,
, R1=nR2, 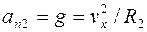 выражение (4) примет вид:
выражение (4) примет вид:
 . (5)
. (5)
Подставляя (5) в (3) получим искомую величину:
cos φ=1/ 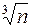 или
или 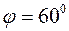 .
.
Ответ: 1. 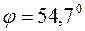 ; 2.
; 2. 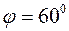 .
.
1.4. Два пловца должны попасть из точки А на одном берегу реки в прямо противоположную точку В на другом берегу. Для этого один из них решил переплыть реку по прямой АВ, другой же – все время держать курс перпендикулярно к течению, а расстояние, на которое его снесет, пройти пешком по берегу со скоростью u. При каком значении u оба пловца достигнут точки В за одинаковое время, если скорость течения 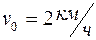 и скорость каждого пловца относительно воды
и скорость каждого пловца относительно воды 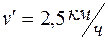 ?
?
Дано: Найти:
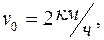
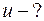
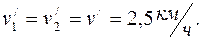
Решение:
Скорость первого пловца относительно берега: 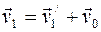 . Скорость второго пловца относительно берега:
. Скорость второго пловца относительно берега: 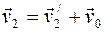 (рис.1.11). Абсолютные величины скоростей первого пловца v1 ивторого пловца v2 относительно берегаможно найти из следующих соотношений:
(рис.1.11). Абсолютные величины скоростей первого пловца v1 ивторого пловца v2 относительно берегаможно найти из следующих соотношений:
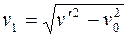 =1,5 км/ч;
=1,5 км/ч; 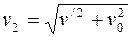 =3,2 км/ч. (1)
=3,2 км/ч. (1)
|
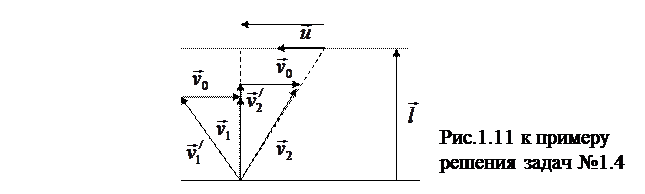
Пусть t - время, за которое пловцы переместились из точки А в точку В; t1 - время, за которое второй пловец переплыл реку, t2 – прошел по берегу со скоростью u. Расстояние s, пройденное вторым пловцом по берегу за время t2 (расстояние, на которое течение снесло второго пловца за время t1):
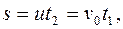 тогда
тогда 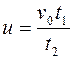 . (2)
. (2)
Расстояние от точки А до точки В можно выразить из следующих соотношений (см. рис.1.11):
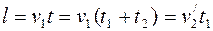 . (3)
. (3)
Выразив из уравнения (3) время t1 и подставив его в (2), получим искомое выражение: 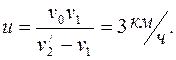
Ответ: